聚类-kmeans以及一些演变

一、作用

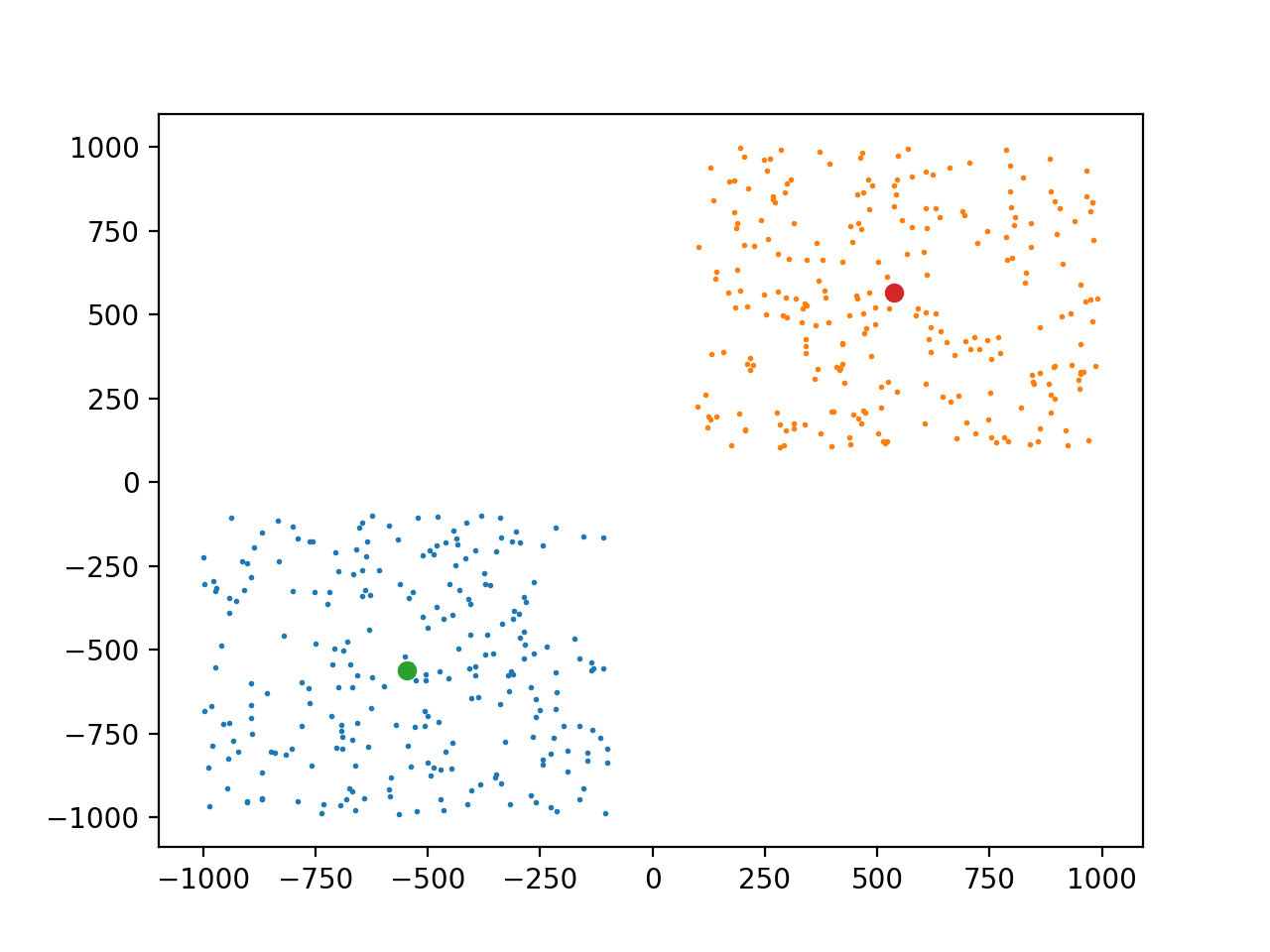
给定一些离散点，然后将这些离散点进行分类，这也叫做聚类。例如，将以下离散点分为两类，中心点也就是绿点和橙色的点也叫做簇心。

 

 

二、步骤

  • 选取k个初始质心（作为初始cluster）；
  • repeat：对每个样本点，计算得到距其最近的质心，将其类别标为该质心所对应的cluster；    重新计算k个cluser对应的质心；
  • 质心的计算方法，将同簇的点，计算它们的平均坐标值作为新的质心　
  • until 质心不再发生变化

 由上可见，kmeans的缺点是聚类的好坏和质心起始位置的选取有关

三、CODE（SKLEARN）

 1 from numpy import *
 2 from sklearn.cluster import KMeans
 3 from sklearn.model_selection import train_test_split
 4 import matplotlib.pyplot as plt
 5 
 6 # create data
 7 n_data = array([[random.randint(100, 1000), random.randint(100, 1000)] for i in range(0, 1000)])
 8 label_n = array([0 for i in range(0, 1000)])
 9 p_data = array([[-1 * random.randint(100, 1000), -1 * random.randint(100, 1000)] for i in range(0, 1000)])
10 label_p = array([1 for i in range(0, 1000)])
11 data_all = concatenate((n_data, p_data), axis=0)
12 label_all = concatenate((label_n, label_p), axis=0)
13 
14 X_train, X_test, y_train, y_test = train_test_split(data_all, label_all)
15 
16 km = KMeans(n_clusters=2)  # 初始化
17 km.fit(X_train, y_train)
18 predict = km.predict(X_test)
19 
20 
21 def accuracy(pred, real):
22     score = 0
23     for i in range(0, len(predict)):
24         if predict[i] == y_test[i]:
25             score += 1
26     return score * 1.0 / len(predict) * 1.0
27 
28 
29 center = km.cluster_centers_
30 
31 fig = plt.figure()
32 ax = fig.add_subplot(111)
33 
34 
35 ax.scatter(data_all[:, 0], data_all[:, 1], s=1)
36 ax.scatter(center[0, 0], center[0, 1])
37 ax.scatter(center[1, 0], center[1, 1])
38 plt.show()

 

四、时间复杂度

时间复杂度为 O(nkl)

  • n为离散点个数
  • k为簇心个数
  • l为迭代次数

 

五、kmeans++

通过概率化的质心选择策略，使初始化质心尽可能分散。流程：

  1. 随机选择一个质心 C1.
  2. 计算每个点到当前点最短距离 D(xi)
  3. 计算下一个点选择质心的概率 P (xi) = D(xi)**2 / sum(D(xj)**2)
  4. 重复2、3选出k个质心

 

  • 六、Capacitated K-Means++

  1. 初始化，选k个中心点
  2. 分配阶段，将每个点分配到最近的中心，如果簇已满，算法学昭下一个最近，且有容量的簇。（贪心，或者其他复杂效果更优的解法）
  3. 更新阶段，根据重新分配的点重新计算中心
  4. 收敛判断，中心点不再变化
posted @ 2019-11-03 12:29  ylxn  阅读(418)  评论(0)    收藏  举报