Python数据结构与算法分析（四、递归）

什么是递归

递归是一种解决问题的方法，他能够将问题分解为规模更小的相同问题，持续分解,直到问题规模可以用非常简单直接的方式解决。

【例】：使用递归求数列 1+2+3+...+99+100 的和

def f(x):
    if x > 0:
        return x + f(x - 1)
    else:
        return 0

递归的三个原则：

• 递归算法必须有基本情况（基本结束条件 ）
• 递归算法必须改变其状态并向基本情况靠近
• 递归算法必须递归的调用自己

【例】整数转换为任意进制的字符串，以十进制769为例，只需对该数按照base进制进行取余（基本结束条件），使用整除不断逼近基本结束条件，然后调用自身进行计算。

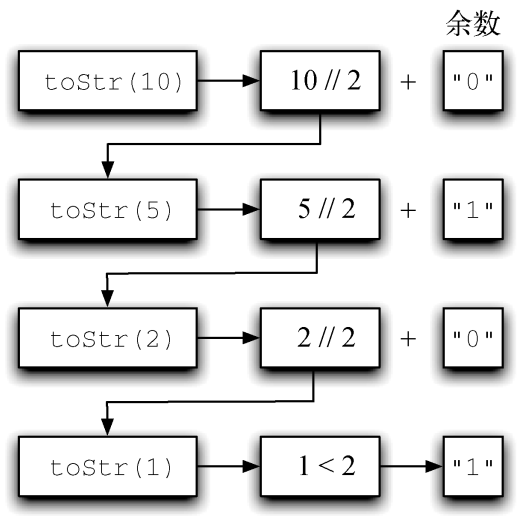
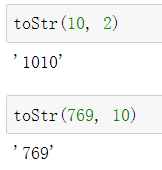
def toStr(intN, base):
    convertString = "0123456789ABCD"
    if intN < base:
        return convertString[intN]
    else:
        return toStr(intN // base, base) + convertString[intN % base]

栈帧

当一个函数被调用的时候，系统会把调用时的现场数据压入到系统调用栈，每次调用，压入栈的现场数据称为栈帧，当函数返回时，要从调用的栈顶取得返回地址，恢复现场，弹出栈帧，按地址返回。

汉诺塔

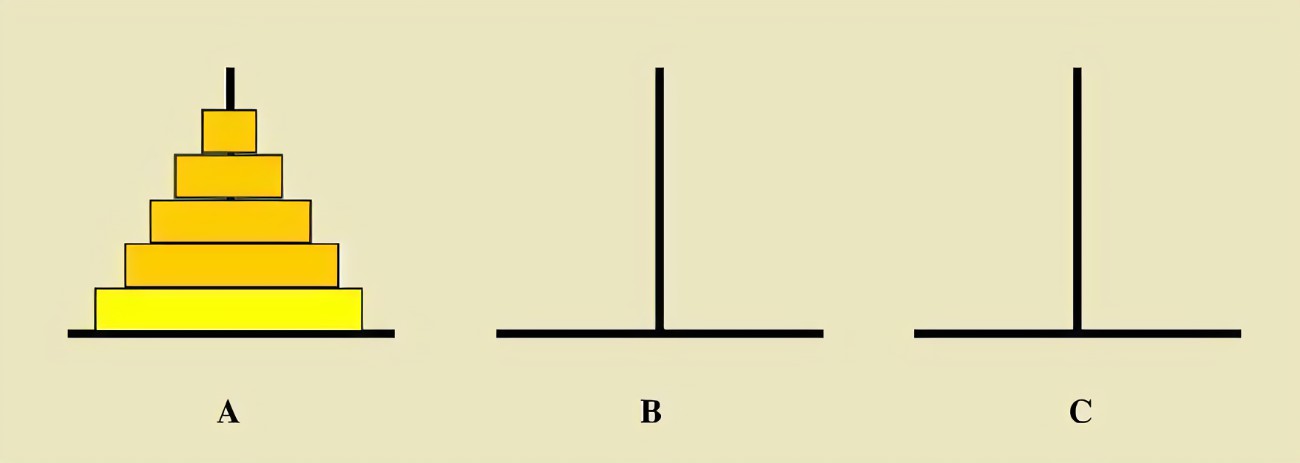
问题可拆解为，如果想将所有的盘子移到C，只需先移动低端的第五个盘子到C，然后将上面的四个盘子移动到B。进一步地，只需将第四块盘子移动到C，将上面的三个盘子移动到A，如此下去... 每次移动都可分为最低端的盘子和上面的盘子两部分来移动。也即：

1. 把 n-1 个盘子从 A 移动到 B

   把第 n 个盘子从 A 移动到 C

2. 把 n-1 个盘子从 B 移动到 C

   ...

def moveTower(n, A, B, C):
    if n == 1:
        print("%d ====> %d" % (A, C))
    else:
        moveTower(n-1, A, C, B)
        print("%d ====> %d" % (A, C))
        moveTower(n-1, B, A, C)