Python数据结构与算法分析(三、基本数据结构)
基本数据结构
基本的数据结构参考第一章导论,下面是四种基本的线性数据结构。
| 线性数据结构是一种有序数据项的集合,其中每个数据项都有唯一的前驱和后继(第一个无前驱,最后一个无后继),新的数据只能加入到某个数据项之前或之后,满足这种性质的数据结构称为线性结构。 |
|---|
1. 栈
1.1 栈的概念及应用
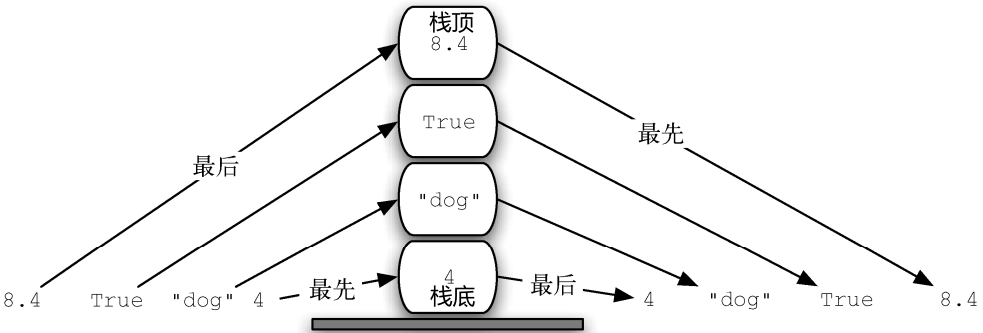
- 排序原则LIFO(后入先出)
- 网页的返回机制,其URL结构为栈,Word的撤销按钮均使用了栈的结构
【Python实现】
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items)-1]
def size(self):
return len(self.items)
【栈的应用】
| 1. 字符串的匹配:编写一个算法,它从左到右读取一个括号串,然后判断其中的括号是否匹配。如 (()()()),((())),(()(()())),则正确,())),((())())则不正确。 |
|---|
def parChecker(parString):
s = Stack()
balance = True
for i in parString:
if i == "(":
s.push(i)
else:
if s.isEmpty():
balance = False
else:
s.pop()
if s.isEmpty() and balance:
return True
else:
return False

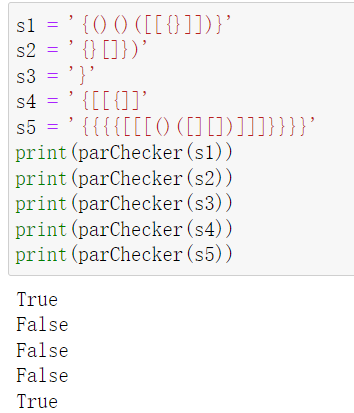
| 2. 字符串的匹配:编写一个算法,它从左到右读取一串字符,然后判断其中的括号是否匹配。如 {()()},[(())],(()(()())),则正确,()]]},{](())())则不正确。 |
|---|
def parChecker(parString):
s = Stack()
balance = True
opens = '{[('
closers = '}])'
for i in parString:
if i in "{[(":
s.push(i)
else:
if s.isEmpty():
balance = False
else:
top = s.pop()
if opens.index(top) != closers.index(i):
balance = False
if s.isEmpty() and balance:
return True
else:
return False
| 3. 将十进制数转换为二进制数 |
|---|
def divideBy2(number):
s = Stack()
binString = ""
while number > 0:
i = number % 2
s.push(i)
number = number // 2
while not s.isEmpty():
binString += str(s.pop())
return binString
1.2 表达式转换
- 全括号表达式转换为后序,向后移动运算符

- 全括号表达式转换为前序,向前移动运算符
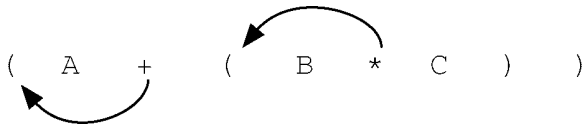
- 从中序到后序的通用转换法
import string
def infixToPostfix(infixExpr):
prec = {"*":3, "/":3, "+":2, "-":2, "(":1}
postString = ""
opstack = Stack()
for i in infixExpr:
if i in string.ascii_uppercase:
postString += i
elif i == "(":
opstack.push(i)
elif i == ")":
a = opstack.pop()
while a != "(":
postString += a
a = opstack.pop()
else:
while (not opstack.isEmpty()) and (prec[opstack.peek()] >= prec[i]):
postString += opstack.pop()
opstack.push(i)
while not opstack.isEmpty():
postString += opstack.pop()
return postString
2. 队列
- 队列是有序集合,添加操作发生在尾部,移除操作发生在头部。新元素从尾部进入队列,然后一直向前移动到头部,直到成为下一个被移除的元素。
- 与栈相反,队列是FIFO(先进先出)

【Python实现】
class Queue:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def enqueue(self, item):
self.items.insert(0, item)
def dequeue(self):
return self.items.pop()
def size(self):
return len(self.items)
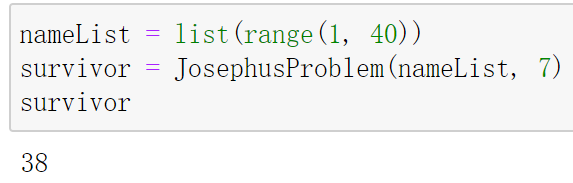
| 1. 约瑟夫斯问题:相传,约瑟夫斯当年和39个战友在山洞中对抗罗马军队。眼看失败,他们决定舍生取义,于是他们围城一个圈,从某个人开始,按顺时针方向杀掉报数为7的人,最后,只有约瑟夫斯自己活了下来,请问,约瑟夫斯刚开始的位置是? |
|---|
def JosephusProblem(nameList,number):
queue = Queue()
for i in nameList:
queue.enqueue(i)
while queue.size() > 1:
for i in range(number):
queue.enqueue(queue.dequeue())
queue.dequeue()
return queue.dequeue()
3. 双端队列
-
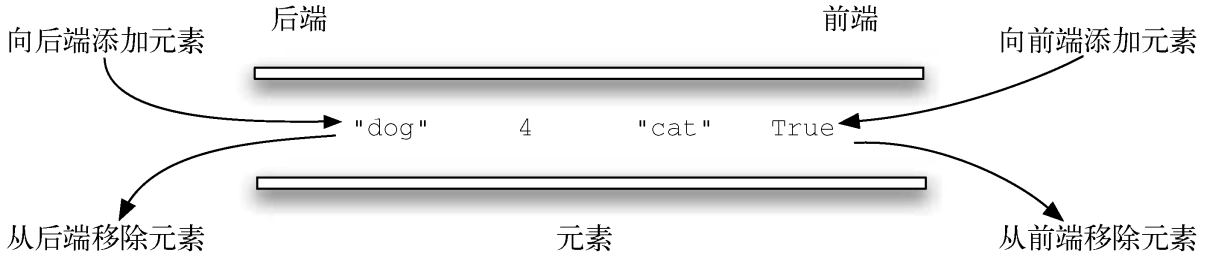
双端队列是与队列类似的有序集合。它有一前,一后两端,元素在其中保持自己的位置。
-
新元素既可以被添加到前端,也可以被添加到后端。
-
已有的元素也能从任意一端移除。
【Python实现】
class Deque:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def addFront(self, item):
self.items.insert(0, item)
def addRear(self, item):
self.items.append(item)
def removeFront(self):
return self.items.pop(0)
def removeRear(self):
return self.items.pop()
def size(self):
return len(self.items)
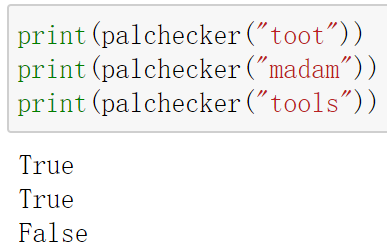
| 1. 回文子串检测:双端队列可以解决一个经典问题,即回文检测器。回文是指从前向后读和从后向前读都一样的字符串。如toot, madam |
|---|
def palchecker(aString):
chardeque = Deque()
for ch in aString:
chardeque.addRear(ch)
stillEqual = True
while chardeque.size() > 1 and stillEqual:
first = chardeque.removeFront()
last = chardeque.removeRear()
if first != last:
stillEqual = False
return stillEqual
4. 链表
- 与前面的顺序表不同,链表是无序结构,连接了内存中的不相连的内存数据。
- 链表中包含两块信息,一块存放数据,另一块指向下一块数据的地址,形成链式结构
4.1 链表的实现
【节点实现】
class Node:
def __init__(self, initdata):
self.data = initdata
self.next = None
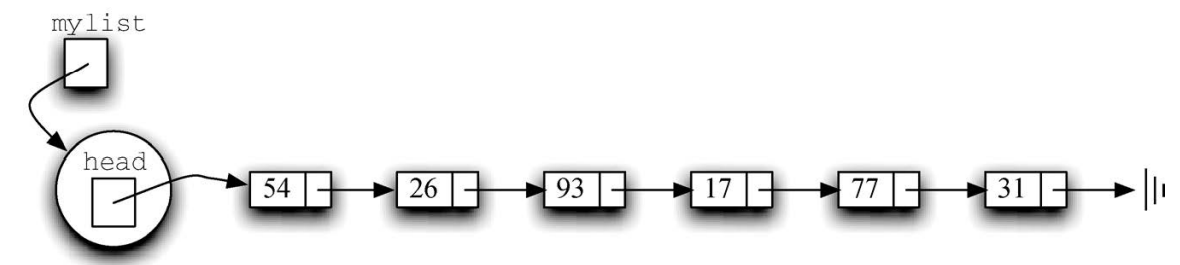
- 无序列表是基于节点集合来构建的,每一个节点都通过显式的引用指向下一个节点;
- 重要的一点,列表类并不包含任何节点对象,而只有指向整个链表结构中第一个节点的引用。
- isEmpty() 判断链表是否为空
- add() 从头部插入元素
- append() 从尾部插入元素
- insert() 指定元素位置插入元素
- remove() 从链表中移除元素(移除第一个查到的相同元素)
- length() 返回链表的长度
- search() 查找链表中是否存在某元素
- travel() 遍历打印链表
class SingleLinkList:
def __init__(self):
self.head = None
def isEmpty(self):
return self.head == None
def add(self, item):
"""头插法"""
temp = Node(item)
temp.next = self.head
self.head = temp
def append(self, item):
"""尾插法"""
node = Node(item)
if self.isEmpty():
self.head = node
else:
current = self.head
while current.next != None:
current = current.next
current.next = node
def insert(self, pos, item):
"""
:param pos: 要插入的位置
:param item: 插入的元素
:return: None
"""
if pos <= 0:
self.add(item)
elif pos > (self.length() - 1):
self.append(item)
else:
pre = self.head
count = 0
while count < pos - 1:
count += 1
pre = pre.next
node = Node(item)
node.next = pre.next
pre.next = node
def remove(self, item):
current = self.head
pre = None
found = False
while not found:
if current.data == item:
found = True
else:
pre = current
current = current.next
if pre == None:
self.head = current.next
else:
pre.next = current.next
def length(self):
current = self.head
count = 0
while current != None:
count += 1
current = current.next
return count
def search(self, item):
current = self.head
while current != None:
if current.data == item:
return True
else:
current = current.next
return False
def travel(self):
current = self.head
while current != None:
print(current.data)
current = current.next
if __name__ == "__main__":
sll = SingleLinkList()
print(sll.isEmpty())
print(sll.length())
sll.insert(0, 100)
sll.add(100)
sll.travel()
sll.remove(100)
print("===========")
sll.travel()
print(sll.isEmpty())
4.2 链表与顺序表
链表失去了顺序表随机读取的优点,同时链表由于附加有地址信息,相应的空间消耗也会增大,但是对于一个较大的数据,链表能够灵活的调用不连续的内存空间,使用相对灵活。
| 操作 | 链表 | 顺寻表 |
|---|---|---|
| 访问元素 | \(O(n)\) | \(O(1)\) |
| 头部插入 | \(O(1)\) | \(O(n)\) |
| 尾部插入 | \(O(n)\) | \(O(1)\) |
| 中间插入 | \(O(n)\) | \(O(n)\) |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号