算法练习(11)-二叉树的各种遍历
二叉树的节点结构如下:
public class TreeNode {
public TreeNode left;
public TreeNode right;
public int val;
public TreeNode(int val) {
this.val = val;
}
public TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return this.val + "";
}
}
一、递归序
二叉树的三种经典遍历: 前序/中序/后序 可参考先前的文章:数据结构C#版笔记--树与二叉树, 不过今天换一种角度来理解"前序/中序/后序"(来自左程云大佬的视频分享), 假设有一个递归方法, 可以遍历二叉树:
public static void foo(TreeNode n1) {
if (n1 == null) {
return;
}
System.out.printf("(1):" + n1.val + " ");
foo(n1.left);
System.out.printf("(2):" + n1.val + " ");
foo(n1.right);
System.out.printf("(3):" + n1.val + " ");
}
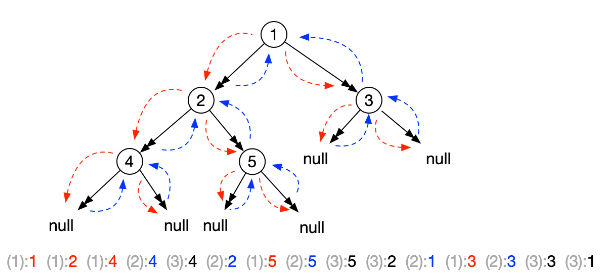
如上图,可以看到,每个节点有3次被访问到的时机,第1次是递归压入堆栈,另外2次是左、右子节点处理完毕,函数返回。
如果在这3个时机,均打印节点的值,会发现:第1次打印的值(上图底部的红色输出),就是前序遍历(头-左-右),第2次打印的值(上图底部的蓝色输出),就是中间遍历(左-头-右),第3次打印的值(上图底部的黑色输出),就是后序遍历(左-右-头).这3次打印结果的全集, 也称为"递归序".
二、前序/中序/ 后序遍历的非递归实现
/**
* 前序遍历(非递归版): root-left-right
*
* @param root
*/
static void preOrderUnRecur(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
stack.add(root);
while (!stack.isEmpty()) {
TreeNode n = stack.pop();
System.out.print(n.val + " ");
if (n.right != null) {
stack.add(n.right);
}
if (n.left != null) {
stack.add(n.left);
}
}
}
/**
* 中序遍历(非递归版): left-root-right
* 思路: 不停压入左边界(即:头-左),直到null,
* 然后弹出打印过程中,发现有右孩子,则压栈
* 然后再对右孩子,不停压入左边界
* @param n
*/
static void inOrderUnRecur(TreeNode n) {
Stack<TreeNode> stack = new Stack<>();
while (n != null || !stack.isEmpty()) {
if (n != null) {
//左边界进栈,直到最末端
stack.push(n);
n = n.left;
} else {
//跳到右边,压入右节点(压完后,n不为空,会重新进入上面的左边界处理)
n = stack.pop();
System.out.print(n.val + " ");
n = n.right;
}
}
}
/**
* 后序遍历(非递归版): left-right-root
*
* @param root
*/
static void postOrderUnRecur(TreeNode root) {
if (root == null) {
return;
}
Stack<TreeNode> stack = new Stack<>();
//用于收集最后所有"排好序"的节点
Stack<TreeNode> result = new Stack<>();
stack.add(root);
while (!stack.isEmpty()) {
TreeNode n = stack.pop();
result.add(n);
if (n.left != null) {
stack.add(n.left);
}
if (n.right != null) {
stack.add(n.right);
}
}
while (!result.isEmpty()) {
System.out.print(result.pop().val + " ");
}
}
三、层序遍历
即按一层层遍历所有节点, 直接按头-左-右, 放到队列即可
public static void levelOrder(TreeNode n1) {
if (n1 == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(n1);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.printf(node.val + " ");
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
}
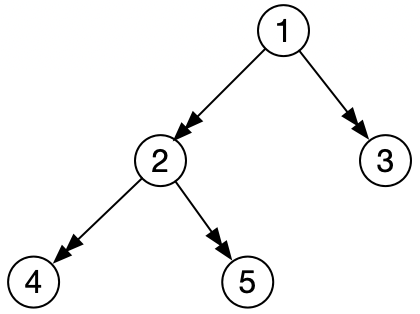
还是这颗树,层序遍历输出结果为 1 2 3 4 5,如果想输出结果更友好点,一层输出一行, 可以改进一下,搞一个Map<Node, Integer> 记录每个节点所在的层
static void levelOrder2(TreeNode n) {
if (n == null) {
return;
}
int currLevel = 1;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(n);
//弄1个map,记录每个元素所在的层
Map<TreeNode, Integer> levelMap = new HashMap<>();
levelMap.put(n, 1);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
//从map取查找出队元素所在的层
int nodeLevel = levelMap.get(node);
//如果与当前层不一样,说明来到了下一层(关键!)
if (currLevel != nodeLevel) {
currLevel += 1;
//输出换行符
System.out.println();
}
System.out.print(node.val + " ");
if (node.left != null) {
//左节点入队,说明取到了下层,把下层元素提前放入map
levelMap.put(node.left, currLevel + 1);
queue.add(node.left);
}
if (node.right != null) {
//右节点入队,说明取到了下层,把下层元素提前放入map
levelMap.put(node.right, currLevel + 1);
queue.add(node.right);
}
}
}
输出为:
1
2 3
4 5
这个版本还可以继续优化, 仔细想想, 其实只需要知道什么时候进入下一层就可以了, 没必要搞个Map记录所有节点在第几层, 按头-左-右的顺序层层入队, 然后不断出队, queue中同时最多也只会有3个元素.
static void levelOrder3(TreeNode n) {
if (n == null) {
return;
}
//curEnd:本层最后1个节点
//nextEnd:下层最后1个节点
TreeNode curEnd = n, nextEnd = null;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(n);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.printf(node.val + " ");
//逐层入队
//注:queue中,最多只会有头-左-右 3个节点
//入队过程中,nextEnd最终肯定会指向本层最后1个节点
if (node.left != null) {
queue.add(node.left);
nextEnd = node.left;
}
if (node.right != null) {
queue.add(node.right);
nextEnd = node.right;
}
if (node == curEnd) {
//如果出队的元素, 已经是本层最后1个,说明这层到头了
System.out.printf("\n");
//进入下一层后,重新标识curEnd
curEnd = nextEnd;
}
}
}
输出效果不变, 层序遍历, 可以演化出很多面试题, 比如:
怎么打印出一颗二叉树每层的序号, 每层最后1个节点的值 , 每层的节点数, 以及整颗树的最大宽度?
无非就是在刚才这个版本上, 再加几个变量, 统计一下而已.
/**
* 打印每层的 层数,本层最后1个节点值,本层节点数, 以及最大宽度
*
* @param n
*/
static void printLevelInfo(TreeNode n) {
if (n == null) {
return;
}
TreeNode curEnd = n, nextEnd = null;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(n);
int currLevel = 1, currLevelNodes = 0, maxLevelNodes = 0;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
currLevelNodes++;
if (node.left != null) {
queue.add(node.left);
nextEnd = node.left;
}
if (node.right != null) {
queue.add(node.right);
nextEnd = node.right;
}
if (node.equals(curEnd)) {
System.out.println("level:" + currLevel + ",lastNode:" + curEnd.val + ",levelNodes:" + currLevelNodes);
currLevel++;
curEnd = nextEnd;
maxLevelNodes = Math.max(currLevelNodes, maxLevelNodes);
currLevelNodes = 0;
}
}
maxLevelNodes = Math.max(currLevelNodes, maxLevelNodes);
System.out.printf("maxLevelNodes:" + maxLevelNodes);
}
再比如:如何判断一颗树是完全二叉树?
分析:完全二叉树的特点,除最后一层外,其它各层都是满的,且最后一层如果出现未满的情况,叶节点只能在左边,即只能空出右节点的位置。
/**
* 判断是否完全二叉树(complete binary tree)
*
* @param n
*/
static boolean isCBT(TreeNode n) {
if (n == null) {
return true;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(n);
//标记是否出现过,仅左孩子的情况
boolean onlyLeftChild = false;
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
TreeNode left = node.left;
TreeNode right = node.right;
//核心判断
if (
//有右无左的情况,非完全二叉树
(right != null && left == null)
||
(
//如果已经遇到过仅左孩子的情况, 后面必须都是叶节点
onlyLeftChild && (right != null || left != null)
)
) {
return false;
}
if (left != null) {
queue.add(left);
}
if (right != null) {
queue.add(right);
}
if (left != null && right == null) {
//标识遇到只有子孩子的情况
onlyLeftChild = true;
}
}
return true;
}
继续:如何获取二叉树中,每个子节点到根节点的路径?

比如这颗树,每个子节点到根的路径为:
4->2->1
5->2->1
6->3->1
7->3->1
2->1
3->1
同样,还是在层次遍历的基本上, 加2个map即可:
/**
* 获取每个节点到根节点的全路径
* @param node
* @return
*/
public static Map<TreeNode, List<TreeNode>> getToRootPath(TreeNode node) {
if (node == null) {
return null;
}
//记录每个节点->父节点的1:1映射
Map<TreeNode, TreeNode> parentMap = new HashMap<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(node);
parentMap.put(node, null);
while (!queue.isEmpty()) {
TreeNode n = queue.poll();
if (n.left != null) {
queue.add(n.left);
parentMap.put(n.left, n);
}
if (n.right != null) {
queue.add(n.right);
parentMap.put(n.right, n);
}
}
//根据parentMap,整理出完整的到根节点的全路径
Map<TreeNode, List<TreeNode>> result = new HashMap<>();
for (Map.Entry<TreeNode, TreeNode> entry : parentMap.entrySet()) {
TreeNode self = entry.getKey();
TreeNode parent = entry.getValue();
//把当前节点,先保护起来
TreeNode temp = self;
List<TreeNode> path = new ArrayList<>();
while (parent != null) {
//辅助输出
System.out.printf(self.val + "->");
path.add(self);
self = parent;
parent = parentMap.get(self);
if (parent == null) {
//辅助输出
System.out.printf(self.val + "\n");
path.add(self);
}
}
result.put(temp, path);
}
return result;
}
输出:
3->1
4->2->1
5->2->1
2->1
6->3->1
7->3->1
{3=[3, 1], 4=[4, 2, 1], 1=[], 5=[5, 2, 1], 2=[2, 1], 6=[6, 3, 1], 7=[7, 3, 1]}
最后贴一个左神给的福利函数, 直观的打印一颗树
/**
* 直观的打印一颗二叉树
*
* @param n 节点
* @param height 节点所在层数(注:根节点层数为0)
* @param to 节点特征(H表示根节点, △表示父节点在左上方, ▽表示父节点在左下方)
* @param len 节点打印时的最大宽度(手动指定)
*/
static void printTree(TreeNode n, int height, String to, int len) {
if (n == null) {
return;
}
printTree(n.right, height + 1, "▽", len);
String val = to + n.val + to;
int lenV = val.length();
int lenL = (len - lenV) / 2;
int lenR = len - lenV - lenL;
val = getSpace(lenL) + val + getSpace(lenR);
System.out.println(getSpace(height * len) + val);
printTree(n.left, height + 1, "△", len);
}
static String getSpace(int num) {
String space = " ";
StringBuilder buf = new StringBuilder();
for (int i = 0; i < num; i++) {
buf.append(space);
}
return buf.toString();
}
用法示例:
static TreeNode init() {
TreeNode n1 = new TreeNode(4);
TreeNode n2_1 = new TreeNode(2);
TreeNode n2_2 = new TreeNode(6);
TreeNode n3_1 = new TreeNode(1);
TreeNode n3_2 = new TreeNode(3);
TreeNode n3_3 = new TreeNode(5);
TreeNode n3_4 = new TreeNode(7);
n1.left = n2_1;
n1.right = n2_2;
n2_1.left = n3_1;
n2_1.right = n3_2;
n2_2.left = n3_3;
n2_2.right = n3_4;
return n1;
}
public static void main(String[] args) {
TreeNode root = init();
printTree(root, 0, "H", 10);
}
输出:
▽7▽
▽6▽
△5△
H4H
▽3▽
△2△
△1△
把头侧过来看, 就是一颗树
作者:菩提树下的杨过
出处:http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
出处:http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号