Top Tree 理论

这应该是我学习的最后一个还在我舒适圈的算法了。后面那一些和数学强相关的算法都很没意思。

建议阅读。推荐阅读。

图源皆是上面的，侵删。

簇（cluster）

基于分治思想将树分成可以递归合并的结构，称之为簇。

类比区间，我们希望一个簇可以只有两个出点。称向外出的点为界点。

簇体现在树上就是一个子树（无根树的子树），称两界点间的路径为簇路径。

参考 base segment 是单点，base cluster 就是一条边。

考虑 merge。compress 是 merge 掉 2-deg 的点，rake 是 merge 掉 1-deg 的点。

把上面的点替换成簇是相同的，因为上面的 merge 操作都保证了簇的性质。

假如每次都尽量去 merge，会得到一棵树，称之为 Top Tree。

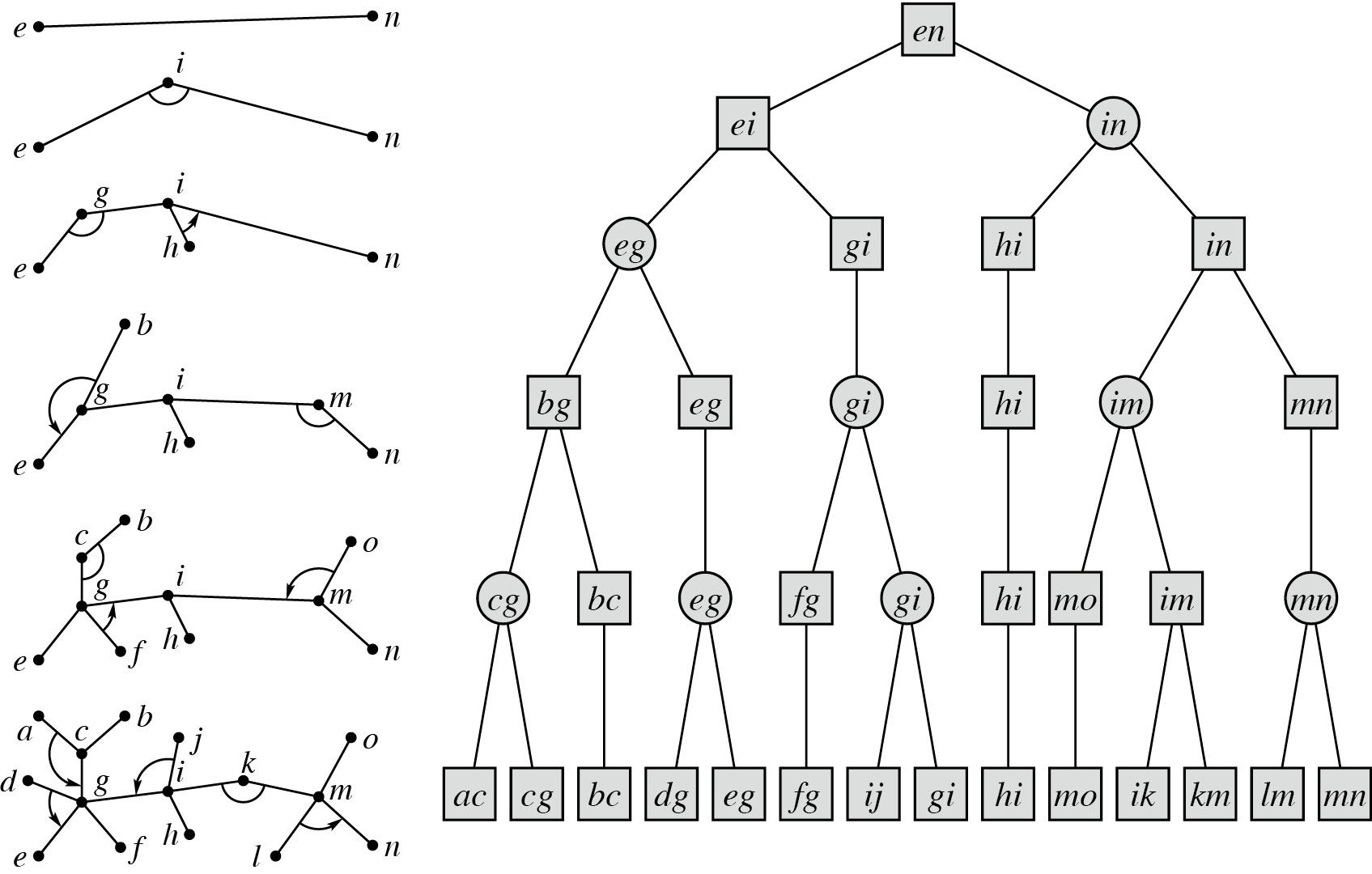
静态 Top Tree

我们对静态 Top Tree 其实已经有所了解。

为了使 Top Tree 树高 log，我们使用重链剖分。还是使用实虚来称呼轻重链。

所有虚子树都会并为一个簇，所以虚子树到实链都是 rake 操作。实链上的点会被 compress 起来，最优的 compress 就是带权中点划分。

不难发现这就是基于全局平衡二叉树的重链重构树。全局平衡二叉树详见我前面写过的链分治学习笔记。

rake tree 就是我提到的重链压缩树，compress tree 就是每个重链的 BST，Top Tree 就是我提到的重链重构树。

值得一题的是 rake tree 的三度化。先 rake 儿子的所有簇，再 rake 进重链就可以实现 rake tree 的三度化。

SATT 实现的动态 Top Tree

上面是重链剖分缩出来的 Top Tree，那要让 Top Tree 动态起来只需要实链剖分即可。

实链剖分的话不难想到 LCT，这里给出基于 LCT 维护的 Top Tree，又称 SATT。

将 LCT 改造成三叉树。实链节点的中儿子表示的是虚子树 rake 起来的节点。

这里注意区分 rake 节点和 compress 节点。事实是对每个 rake 操作建一个 rake 结点就可以使 Top Tree 三度化。

换句话说，compress 结点包含了所有 rake 节点并的中儿子，而 rake 节点中儿子连接一棵 compress tree。

实现和 LCT 其实很象，唯一不同的是注意 access 操作。

Top Cluster 树分块

借用 Top Tree 理论，我们可以给出满足以下性质的树分块：

1. 将树分成大小为 \(B\) 的簇，总共 \(\frac{n}{B}\) 个。
2. 划分了树的边集。
3. 簇路径是自上而下的链。
4. 内点属于唯一簇。
5. 一个界点是一个簇的下界点和多个簇的上界点。
6. 界点相连可以构成压缩树。

构建

随便取根，强令根为界点。

然后 dfs，用栈存储未归类的边。当发生以下情况时需要对边划分成簇：

1. \(u\) 为根。
2. \(u\) 有两个子树有界点。
3. 栈大小超过 \(B\)。

划分时尽量选栈的一段前缀，当遇到以下三种情况时出栈：

1. \(u\) 的子树用完。
2. 新加子树会出现两个界点。
3. 新加子树大小会超过 B。

证明略。