换根 & 树形

$\large\color{skyblue}\textbf{\textsf{简介}}$

其实就是在树上 DP，由于树固有的递归性质，树形 DP 一般都是递归进行的。

$\large\color{skyblue}\textbf{\textsf{树形 DP}}$

一般而言，有如下模板可以套用。

void dfs(int from,int fa) {
	for(遍历与from相连的边) {
		if(to==fa) {
			continue; 
		}
		dfs(to,from);
		使用 dp[to] 更新 dp[from]; 
	}
}

讲解一道模板题，了解树形 DP 使用方法。

P1352 没有上司的舞会

在本题中，定义 $dp$ 如下：

• $dp_{from,0}$：以 $from$ 为根的子树，$from$ 不参加的最大快乐指数。
• $dp_{from,1}$：以 $from$ 为根的子树，$from$ 参加的最大快乐指数。

接下来探究状态转移方程：

• 对于 $from$ 不参加，$from$ 的儿子参加与否均可。
• 对于 $from$ 参加，$from$ 的儿子只能不参加。

定义集合 $S$ 包含 $from$ 的儿子，方程表示为：

$$dp_{from,0}=\sum\limits_{to\in S(from)}\max(dp_{to,0},dp_{to,1})$$ $$dp_{from,1}=\sum\limits_{to\in S(from)}dp_{to,0}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \$$

$\large\color{skyblue}\mathcal{Code}$

#include<bits/stdc++.h>
using namespace std;
const int N=6e3+10;
struct edge{
	int to,next;
}ee[N<<1];//两倍 
int head[N],ne;
void ae(int from,int to) {//链式前向星 
	ee[++ne]={to,head[from]};
	head[from]=ne;
}
int n,w[N],dp[N][2];
void dfs(int from,int fa) {
	dp[from][1]=w[from];//设置初始状态 
	for(int i=head[from];i;i=ee[i].next) {
		int to=ee[i].to;
		if(to==fa) continue;//防止重复访问 
		dfs(to,from);//递归求解 dp[to] 
		//更新 
		dp[from][0]+=max(dp[to][0],dp[to][1]);
		dp[from][1]+=dp[to][0];
	}
}
int main() {
	cin>>n;
	for(int i=1;i<=n;i++) cin>>w[i];
	for(int i=1,x,y;i<n;i++) {
		cin>>x>>y;
		ae(y,x),ae(x,y);
	}
	dfs(1,0);
	//最后要在两个合法状态中取最大 
	cout<<max(dp[1][0],dp[1][1]);
	return 0;
}

有一个小提醒：用链式前向星存图要两倍！

$\large\color{skyblue}\textbf{\textsf{换根法（二次扫描）}}$

$\color{skyblue}\textbf{\textsf{引入}}$

有些情况，对于不同的根，有不同的答案。对每个点树形 dp，太慢。

此时就可以通过已知的根在较快（一般为 $O(1)$）求出一个新根的答案。

和树形 dp 不一样的地方在于：

• 树形 dp 通过儿子得出当前点。
• 换根 dp 通过父节点得出儿子。

模板为：

void dfs(int from,int fa) {
	for(遍历与from相连的边) {
		if(to==fa) {
			continue; 
		}
		dfs(to,from);
		使用 dp[to] 更新 dp[from]; 
	}
}
void ddfs(int from,int fa) {
	for(遍历与from相连的边) {
		if(to==fa) {
			continue; 
		}
		使用 dp[from] 更新 dp[to];
		dfs(to,from); 
	}
}
/*
还有另外一种写法，本质上都是通过已知的更新未知。 
void ddfs(int from,int fa) {
	if(from不是根) {
		使用 dp[fa] 更新 dp[from];
	}
	for(遍历与from相连的边) {
		if(to==fa) {
			continue; 
		}
		dfs(to,from); 
	}
}
*/

同样讲解一道模板题。

P3478 STA-Station

根据题意得出，根为 $1$ 时，深度和为 $\sum\limits_{x\in T} s_{x}$。 其中 $s_{from}$ 为以 $from$ 为 $1$ 为树的根节点，$from$ 的子树节点个数。我们可以定义 $dp_{from}$ 为以 $from$ 为根的树深度和。根据定义得 $dp_1\gets \sum\limits_{x\in T} s_{x}$。接下来思考如何转移。

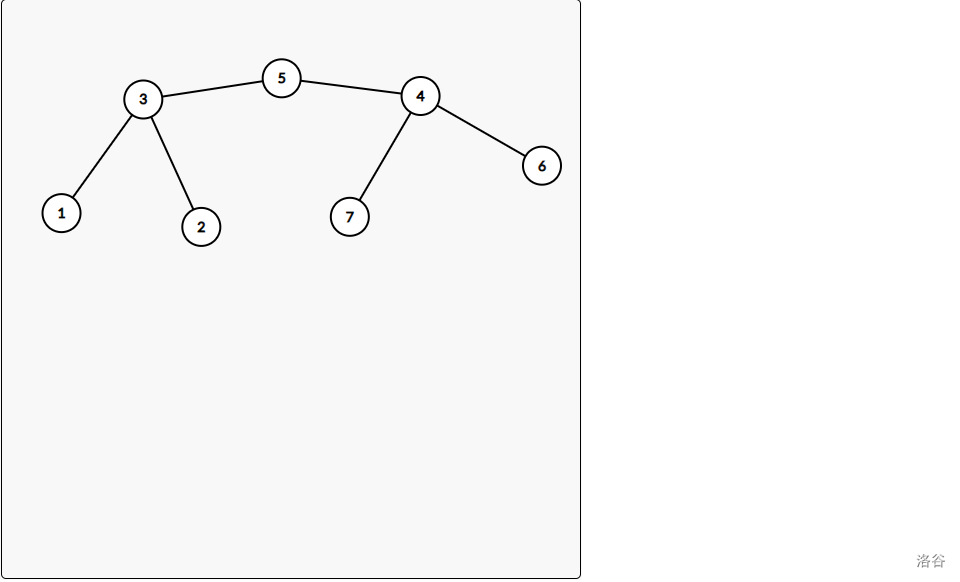此时树的根在 $5$，假设 $5$ 已经被求出来了。

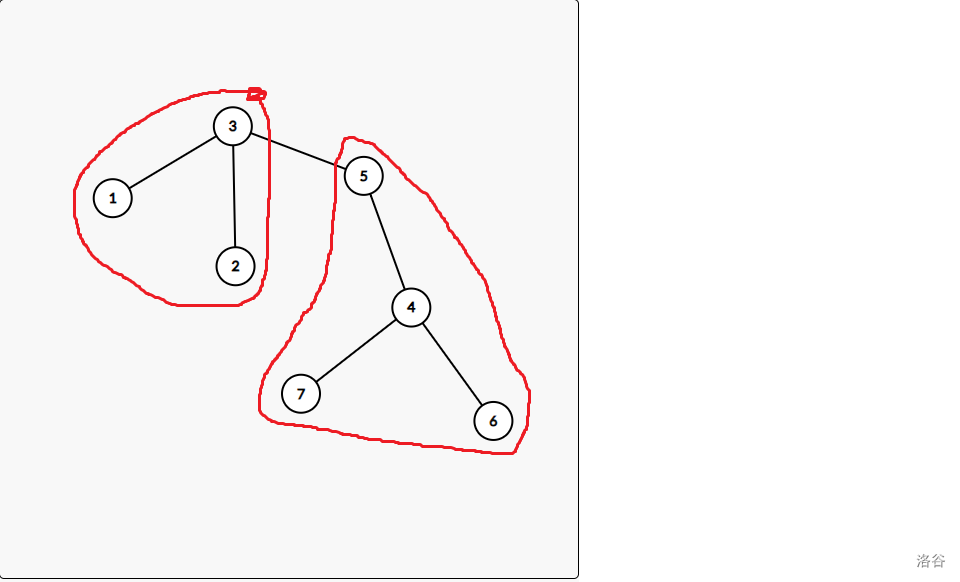此时可以通过 $dp_5$ 来更新 $dp_3$。将树分为两个部分。

• 对于 $3$ 的子树，里面的每个点，深度都被减少了 $1$，即 $-s_{3}$
• 对于不属于 $3$ 的节点，这些节点共有 $n-s_3$ 个，他们的深度都增加了 $1$。

---

所以可以得出状态转移方程为：

$$dp_{to}=dp_{from}-s_{to}+(n-s_{to})$$ $$dp_{to}=dp_{from}-2\times s_{to}+n\ \ \ \ \$$

$\large\color{skyblue}\mathcal{Code}$

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6+10;
struct edge{
	int to,next;
}ee[N*2];
int up[N],head[N],ne,s[N],f[N];
int n;
void ae(int from,int to) {
	ee[++ne]={to,head[from]};
	head[from]=ne;
}
void dfs(int from) {
	s[from]=1;
	for(int i=head[from];i;i=ee[i].next) {
		int to=ee[i].to;if(s[to]) continue;
		dfs(to);
		s[from]+=s[to];
	}
}
void dfss(int from,int fa) {
	for(int i=head[from];i;i=ee[i].next) {
		int to=ee[i].to;
		if(to==fa) continue;
		f[to]=f[from]-s[to]*2+n;
		dfss(to,from);
	}
}
signed main() {
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1,x,y;i<n;i++) {
		cin>>x>>y;
		ae(x,y),ae(y,x);
	}
	dfs(1);
    for(int i=1;i<=n;i++) f[1]+=s[i];
	dfss(1,0);
	int ans=0;
	for(int i=1;i<=n;i++) {
		if(f[i]>f[ans]) ans=i;
	}
	cout<<ans;
	return 0;
}