wqs 二分小记

前言

由王钦石发明，也叫 Ailen trick。

适用范围

对于这样的问题：有若干个物品，选一些（有某些限制），问最（最大或最小）价值是多少。对于这个限制，可能是要求恰好选 $m$ 个。

对问题有这样的要求：

1. 如果没有限制，解决起来简单，并且还要知道取了多少个。
2. 设恰好取 $i$ 个物品的最优价值为 $w(i)$。在平面直角坐标系中，所有 $(i,w(i))$ 形成凸包。

---

思路

为什么要有第一条呢？因为算法的思想是将某些物品修改，使得选择不受限，再把修改的影响消除。

以下为上凸包的情况：

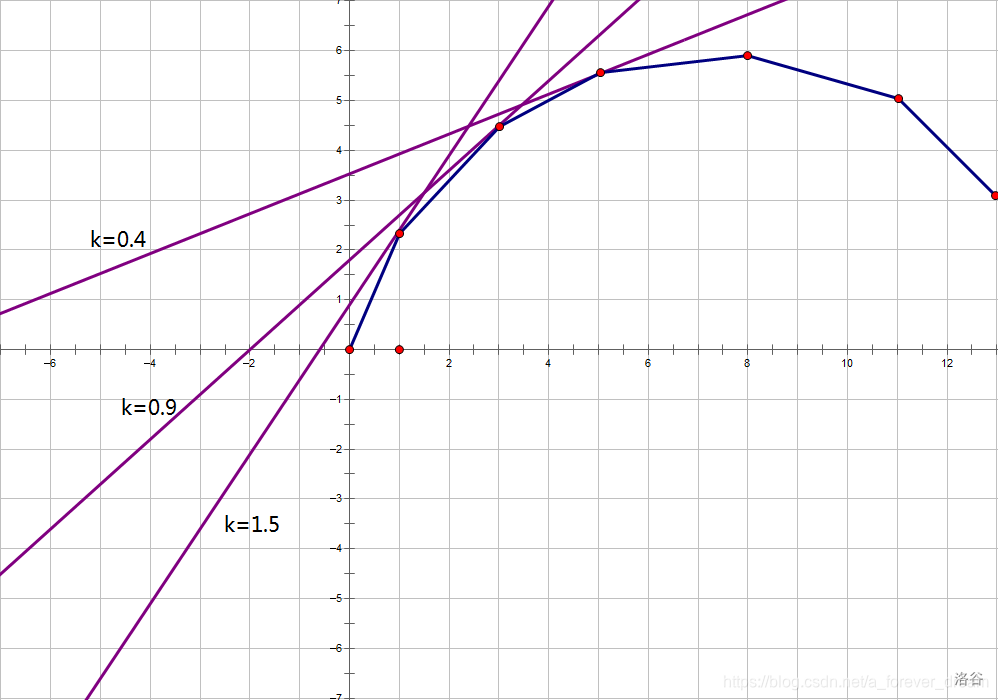
我们只知道它的形状，但是哪个值最大（即为答案）呢？或者每个点具体的值？这是我们需要计算的。

用一条直线切，二分一下斜率 $k$，会切到至少（后面要讲）一个点，得到一个结论：该直线的截距就是将选取受限制的物品全部减 $k$ 后，将限制取消得到的最优解。

解释一下：

假设我们用斜率为 $k$ 的直线，把与所有点相交的情况都画出来，会发现与凸包相切的直线截距 $b$ 是最大的。（凸包的性质）

考虑一下每个 $b$ 的实际意义，因为 $b=-kx+y$，点 $(x,y)$ 的意义为：取 $x$ 个物品，得到的最优解。$b,y$ 之间差 $-kx$。可以看作当所有物品都减少了 $k$ 时，选 $x$ 个得到的最优解，这是因为每个物品的相对大小不变。

凸包相切的直线截距 $b$ 是最大的，也就是说取 $1\sim n$ 个物品的情况中，取 $x$ 个是最优解。但是指定取 $x$ 个不好求啊！没关系，这就是求全局最优解，直接求。

至此，根据特殊情况下的全局最优解，就可以得到点 $(x,y)$，假设我们的目标是求 $(m,y_m)$，通过凸包的性质，调整 $k$ 的大小就可以求出答案。（如在上凸的情况下，减小 $k$ 就会使得 $x$ 变大，反之则反。）

细节

如果有很多点，他们凸包斜率相同呢？

如果随便求，就会导致即使斜率是对的，但是合法答案被错误地判断成非法。比如：

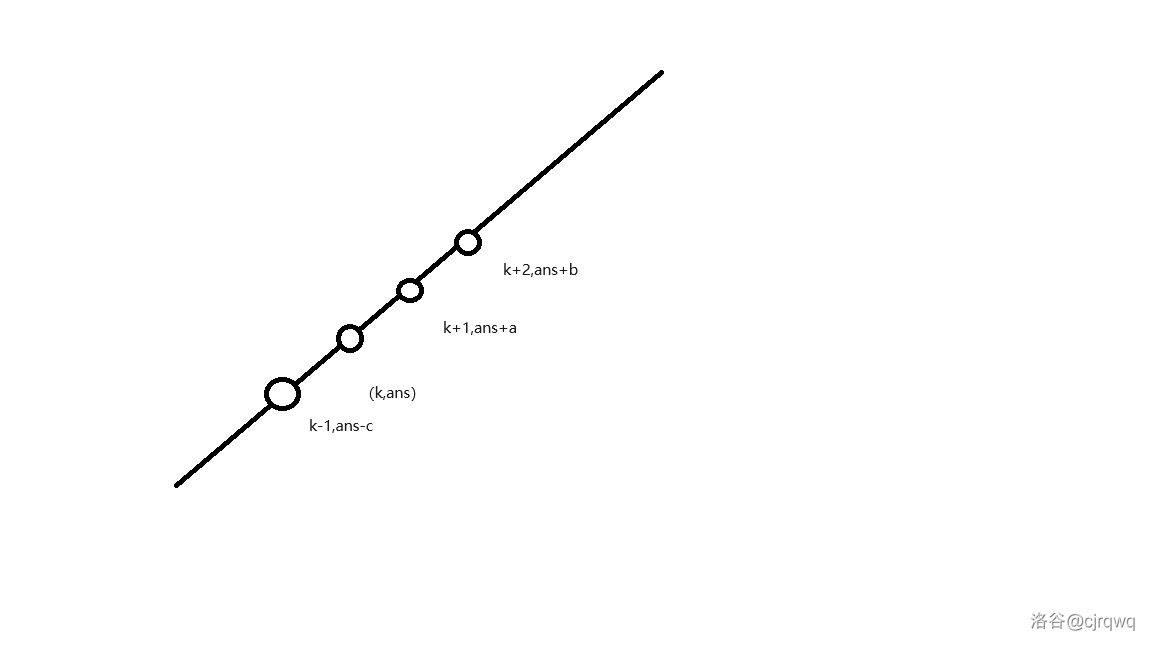
要是求出了 $k+1,k+2$，就会使斜率被修改。

那如果求出了 $k-1$ 呢？其实是没关系的，因为斜率 $k_1$ 还是对的，假如有解，横坐标必定是 $m$。在求答案的时候将 $b + kx$ 改成 $b + km$ 就好了。

---

总结一下：

1. 有限制，想要把限制去除，去除了就可以写。
2. 可以去除，但是不知道为答案去除限制时的 $k$ 是多少。
3. 因为是凸包，所以每个点都会被不同的 $k$ 切到，同时 $k$ 还具有单调性，所以可以二分。
4. 找到答案的 $k$。求出 $y$。