【暑假集训】【平衡树】Splay 小记

引言

已经一个月快没有写博客了，颓。

相比于普通 treap 的 zig 和 zag 操作，splay 多了“双旋”。即连续转两次：zig-zig,zag-zag,zig-zag,zag-zig。

splay 的很大一个特性就是可以快速地将 x 旋转为 y 的儿子或根，其操作也是据此实现。

---

旋转

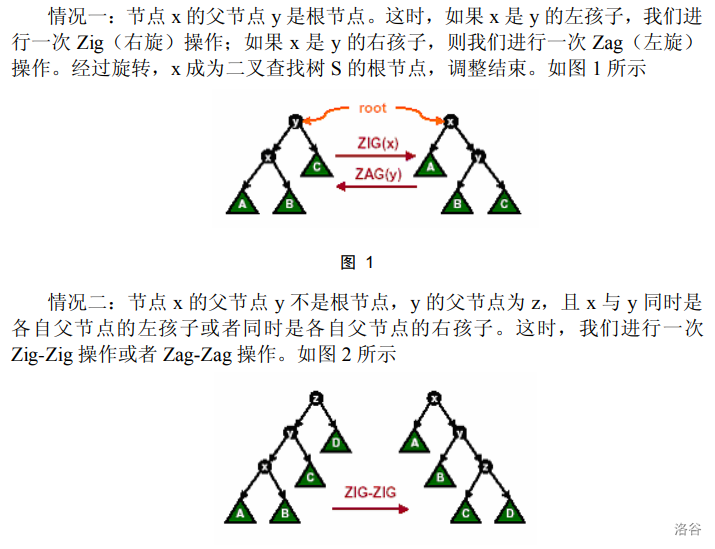
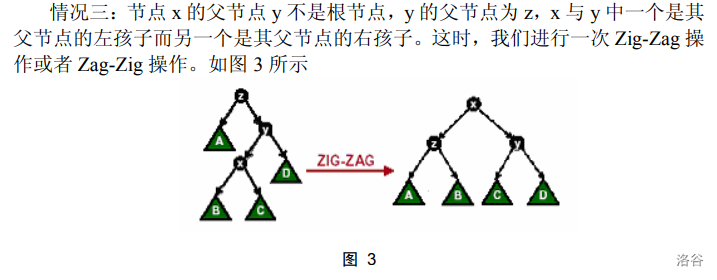
（图片转载，来源为 IOI2004 杨思雨的集训队论文）

注意：zig-zag，zag-zig是连续转两次 $x$。而 zig-zig,zag-zag是先转 $y$ 再转 $x$。

---

操作

以下 rt 的意思是在以 rt 为根的树内。

find(rt,x)

查找是否有 $x$，根据 BST 的性质就好了。

pre(rt,x)

查找前驱。根据 BST 的性质，大了就往左，小了就往右，不断更新答案。

suc(rt,x)

查找后继。和 pre(x) 同理。

Knum(rt,x)

查找第 k 名是哪个点，也是用递归的形式，要注意 x 会随着 rt 的变化而变化，因为要减去已经考虑过的左子树对答案的影响。

---

以下都是关于点的操作，都可以通过 pre,suc 组合实现。

需要注意，无论转起来是否有用，他们都需要转两次，否则复杂度不对。

ins(x)

插入 $x$。我们考虑给 $x$ 放到合适的位置。因为 BST 的性质，如果以前驱为根，后继为前驱的右子树，那么后继的左子树只可能是 $x$ 了，所以直接旋转前驱，后继，再更新 $x$（新建 $x$）。

用代码表示就是 splay(pre,null),splay(suc,splay)

del(x)

删除 $x$。和 ins(x) 同理。

rk(x)

查询 $x$ 的排名。同理旋转后。排名就是根的左子树，根的节点个数的和加一。但是我们发现只要把前驱转到根就好了，为什么要转后继？其实是上面的“注意”中提到的问题。

普通平衡树

特别地，如果面对构造过的数据，即使已经正确旋转了会超时。此时，把每次操作的结果都旋转到根即可。

数据加强版

---

区间翻转

文艺平衡树

假如我们要翻转 $[l,r]$ 这一区间。

我们考虑找到节点 $l-1,r+1$ 并且将它们分别作为根，根的右子树。此时，我们并不按照权值为序，而是按照下标为序。

那么区间 $l,r$ 就会在 $r+1$ 的左子树了。此时，给该节点打一个懒标记，和线段树一样下传标记即可。