高斯消元小记

前言

对于一个二元一次方程。可以把 $y$ 用 $x$ 表示出来，再代入到另一个式子，就可以知道 $x$，再通过 $x$ 可以算出 $y$。

流程

这个过程就是高斯消元法。下面是算法流程。

设每个式子都形如 $a_1x_1+a_2x_2\dots+a_{n-1}x_{n-1}+a_nx_n = S_i$。

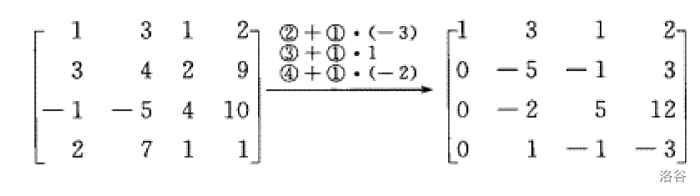
第三个矩阵就是我们在代码里表现出来的形式。

然后，枚举一个 $i$，即主元。再找到一个 $h$，满足 $a_{h,i} \not=0$。将 $i,h$ 行交换，显然，此时 $a_{i,i}=1$ 了。我们就用第 $i$ 行，对除此之外的行进行消元，也就是把第 $i$ 列上的值全部变成 $0$。

如果找不到 $h$ 呢？说明找不到一个对 $x_i$ 有约束的情况，那么必是无数解或无解。

会不会有无解，无数解的情况出现呢？我们在最后统计的时候判断。

• 无解，如果第 $i$ 行的 $a_i$ 为 $0$，但是 $a_{n+1}\ne 0$ ，那么显然不成立，即无解。

• 无数解，如果第 $i$ 行的 $a_i$ 为 $0$，但是 $a_{n+1} = 0$ ，那么对 $a_i$ 没有限制，有无数解。

为什么可以这样判断？因为每一列到最后都只有 $a_{i,i}$ 可能会不等于 $0$。其余列都是已经消除或者缺少主元（本来就一个也没有）。

题目

这是模板题：P2455 [SDOI2006] 线性方程组

练习题：Widget Factory

题解

关于异或版的高斯消元：

P2447 [SDOI2010] 外星千足虫

同时也相当于模 $2$ 意义下的方程组。

利用异或自己就是自己的逆运算的性质，把减号改成异或就好了。还可以用 bitset 加速。