2-SAT 小记

前言

一些约定：$\lor$ 表示逻辑或，$\land$ 表示逻辑与，$\neg x$ 表示 $x$ 取 $0$，$x$ 表示 $x$ 取 $1$。

2-SAT 就是形如 $A=a\lor B=b|a,b=[0,1]$ 的问题。

假如有 $n$ 个这种条件，让我们同时满足呢？

也就是 $(A_1=a\lor B_1 =b) \land (A_2=a\lor B_2 =b) \dots (A_n=a\lor B_n =b)=1|a,b = 0,1,A\in S, B\in S$。

求解

对于一个问题，如果 $A$ 满足条件，$B$ 可以满足或不满足。这是“正”的看法。

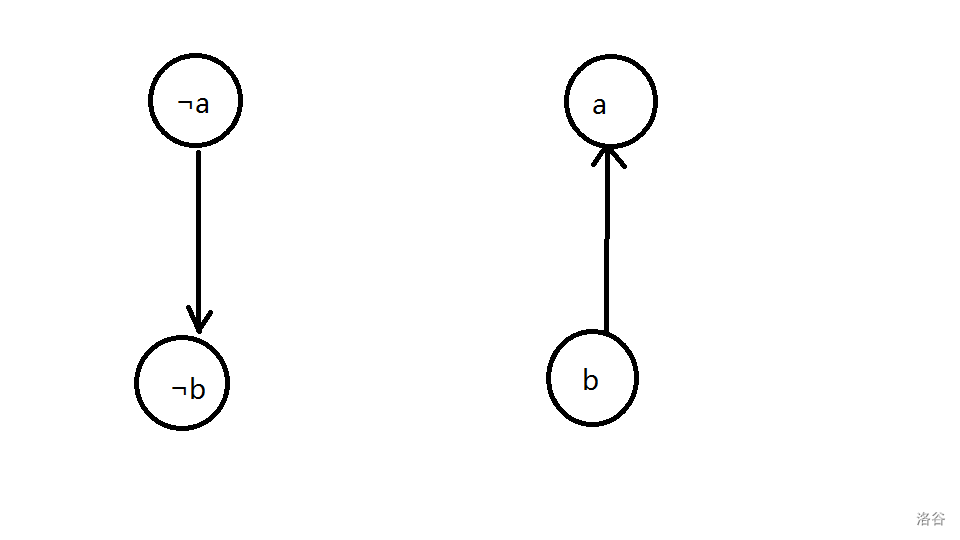
假如反过来呢？如果 $A$ 不满足条件，$B$ 就必须满足条件，同样的，如果 $B$ 不满足条件，$A$ 就必须满足条件。只要满足这个限制，就是合法解。因为带有方向性，并且还是递归性质的，把它用有向图表示出来。以下设 $A = 1\lor B = 0$。

考虑把 $A$ 拆成 $a',a$，分别表示取 $0$，取 $1$。那么图长这样：

接下来也是一个例子：

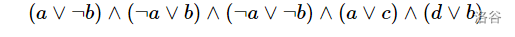
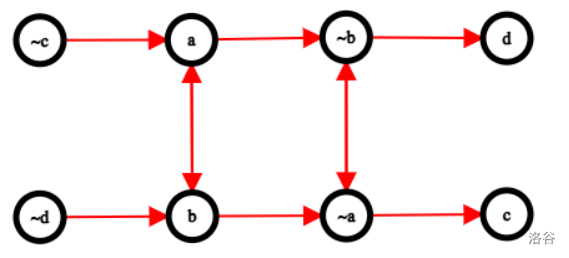
我们会发现，在一个强连通分量中，点是可以互相确定的。因为 $a$ 只能在 $a,\neg a$ 中任选其一，如果 $a$ 和 $\neg a$ 在一个强连通分量中，肯定就是无解的。类似地，$a$ 如果能到达 $\neg a$，说明答案肯定是 $\neg a$ 而非 $a$，否则会产生矛盾。因此，我们可以求出一组解，问题被我们转换为判断两点间的连通关系。

可以缩点，在 DAG 上拓扑排序。事实上，并不需要真正的拓扑排序，缩点算法已经算出了拓扑序。

以我用的 Kosaruju 举例子。每次找强连通分量的时候，都是还没有缩的，拓扑序最小的点，缩成的强连通分量序号也就是拓扑序了。

讲到这里，你是不是觉得和差分约束挺像的？都是一个图论建模，再通过图论算法求解的过程。

---

题目

P4782 【模板】2-SAT
P4171 [JSOI2010] 满汉全席

这两题就是板子题。

P6378 [PA2010] Riddle
[ABC210F] Coprime Solitaire
P3513 [POI2011] KON-Conspiracy

本文的部分图片来自 super蒟蒻 的 PPT，给你发好人卡 ^_^ 。

(*≧ω≦)