【lgj】【DP】【图论】

其实有原题。但是 topcoder。

问题：给定 n 个点的无向图 $G(V,E)$，求满足经过 5 条边，且这 5 条边不重复的路径数量。

$n\le 500$。

先 DP 一下，但是 5 条边都不能重复，显然 DP 不出来。所以我们求不走回头路的方案数，即 $A\to B\nrightarrow A$。

很简单，设 $f^{A,i,j}$ 表示经过 $A$ 个点，倒数第二个经过的是 $i$，最后经过的是 $j$。

然后发现只有三元环，四元环会有重复。

三元环直接枚举 $i,j,k\in V$。

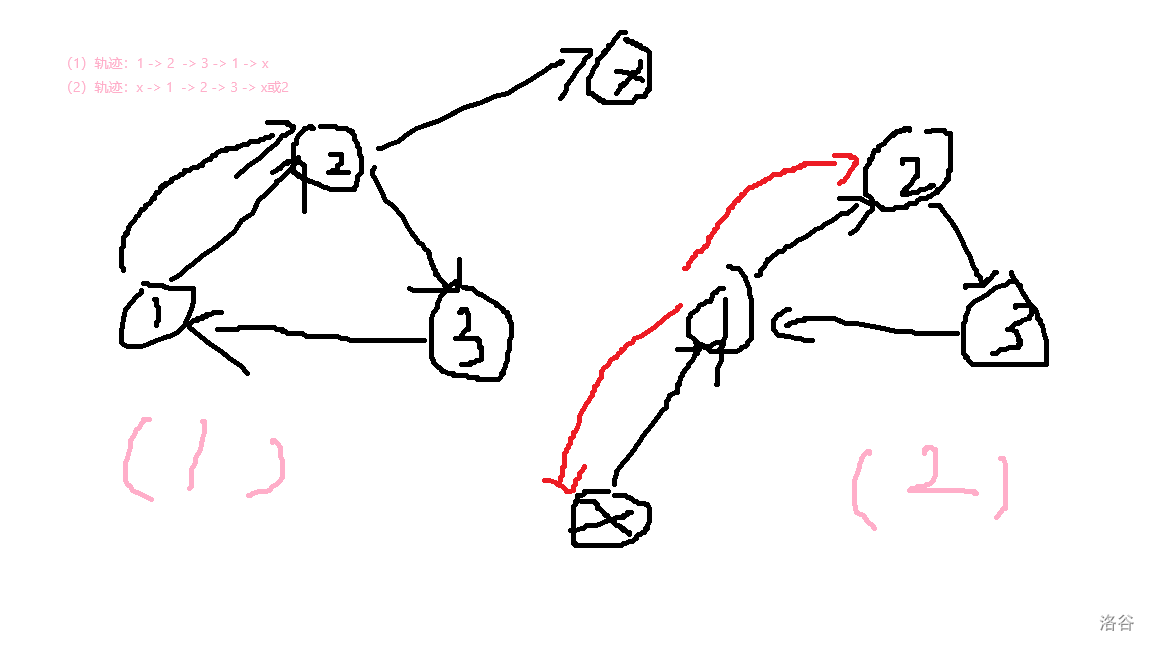
有这么两种情况，情况（1）的 $x$ 可以取除了 $1$ 的任何相连的点，情况（2）的 $x$ 可以取除了 $2,3$ 的任何点。不能取 $3$ 是因为情况（1）已经算过了，相当于 $3\to 1\to 2\to 3\to 1\to x$。其他两个是回头路，DP 不统计。

四元环枚举两个点 $i,j\in V$，找与 $i,j$ 都连边的点，设有 $x$ 个。钦定 i 是第一个，$j$ 是第三个，剩下选第二，四个点，即 $A^x$。只有再走一遍第一个点到第二个点才会重复。

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 520;
int a[N][N],mp[5000000];

int n,state,thr,L;
int tog[N];

int f[7][N][N];

int lb[N],js[N][N];
signed main() {
	cin>>n>>state>>thr>>L;
	for(int i=0;i<L;i++) cin>>tog[i];
	for(int x=0;x<n;x++) {
		for(int y = x+1; y < n; y++) {
			state = (state * 1103515245 + 12345) % (1LL<<31);
			if(state < thr) a[x][y] = a[y][x] = 1, lb[x]++,lb[y]++;
		}
	}
	for(int i=0;i<L/2;i++) {
		int x = tog[i*2], y = tog[i*2+1];
		if(a[x][y]) a[x][y] = a[y][x] = 0,lb[x]--,lb[y]--;
		else a[x][y] = a[y][x] = 1, lb[x]++,lb[y]++;
	}// 用种子生成，逆天输入格式

	for(int x=0;x<n;x++) {
		for(int y=0;y<n;y++) f[2][x][y] = a[x][y];
	}
	for(int d=3;d<=6;d++) {
		for(int i=0;i<n;i++) {
			for(int j=0;j<n;j++) {
				for(int k=0;k<n;k++) {
					if(j == k || i == j || k == i || a[i][j] == 0 || a[k][i] == 0) continue;
					f[d][i][j] += f[d-1][k][i];
				}
			}
		}
	}
	
	int ans1 = 0,aaa=0;
	for(int i=0;i<n;i++) {
		for(int j=0;j<n;j++) {
			for(int k=0;k<n;k++) {
				if(a[i][j] && a[j][k] && a[k][i]) ans1 += lb[j] - 1 + (lb[i] - 2) * 2,aaa ++;
				
				if(a[i][j] && a[k][j] && i != k) js[i][k] ++;
			}
		}
	}
	
	int ans2 = 0;
	for(int i=0;i<n;i++) {
		for(int j=0;j<n;j++) {
			ans2 += js[i][j] * (js[i][j]-1);
		}
	}
	int ans = 0;
	for(int i=0;i<n;i++) {
		for(int j=0;j<n;j++) {
			ans += f[6][i][j];
		}
	}
	cout<<ans-ans1-ans2;
	return 0;
}