2025.10.20 - 10.31

Question 1. 「JOISC 2020 Day3」收获

一个庄园内有一个圆形大湖，湖岸分布着 \(N\) 个员工与 \(M\) 棵苹果树，将大湖的圆周等分成 \(L\) 份，等分点从一点开始顺时针顺次编号为 \(1,2,3,\cdots,L-1,L\)。

第 \(i\) 个员工初始位于点 \(A_i\) 处，第 \(j\) 棵苹果树初始位于点 \(B_j\) 处，每棵苹果树初始都有一个成熟的苹果。

庄园内的苹果树很奇怪，只有当树上的唯一一个成熟的苹果被摘下后的 \(C\) 秒后才有下一个成熟的苹果供人摘取。庄园内的员工也很奇怪，每个员工都以一定的速度（每一秒从一个等分点走到下一个等分点）绕湖顺时针移动。

现在庄园主有 \(Q\) 个询问，第 \(k\) 个询问给出 \(V_k,T_k\)，表示询问直至时刻 \(T_k\) 员工 \(V_k\) 总共摘下了多少个苹果？

\(N,M,Q\leq 2\times 10^5, L,C\leq 10^9, T_k\leq 10^{18}\)，所有的 \(A_i,B_j\) 按升序给出，且全体 \(A_i,B_j\) 共 \(N+M\) 个数两两相异。

首先让我们换一种方式来观察这个问题，每个时刻员工 \(i\) 走到一棵树 \(j\) 下可能可以摘到一个苹果，也有可能还没有长出来，这是不好考虑的。但是每个员工 \(i\) 摘下一个苹果之后，这棵树上的下一个苹果被谁摘下来是确定的，具体的，从位置 \((A_i - C)\bmod L\) 开始再逆时针找到的第一个员工 \(k\)，花费时间就是两员工间的逆时针弧上距离。让 \(i\) 向 \(k\) 连边，由于每个 \(i\) 只连出一条边，这个图就是内向基环树森林。

接下来，考虑一棵苹果树，可以假定人不动，苹果树绕着湖逆时针转起来，一棵树 \(j\) 首先被第一个遇到的员工 \(p\) 摘下，随后就会被 \(p\) 的出边指向的员工 \(q\) 摘下，再然后被 \(q\) 的出边指向的员工 \(r\) 摘下……对于苹果树 \(j\)，设 \(F^e_j\) 为第一个摘下树 \(j\) 上的苹果的员工，设 \(F^t_j\) 为第一次被摘下的时间（这个问题涉及的量太多了，原谅我用这样的记法）。

那么每个询问就很容易来刻画了，每棵苹果树要花费一定时间通过一条边，每到达一个点就使得其点权 \(+1\)，在时刻 \(T_k\) 时询问点 \(V_k\) 的点权。

基环树首先考虑分类讨论，分 \(V_k\) 位于树上还是环上分别处理：

\(V_k\) 是树上的点

由于从一点 \(p\) 开始肯定是一直向环进发，如果没有遇到 \(V_k\) 就不可能遇见了，所以对树上的 \(V_k\) 的询问，本质上是计算有多少个苹果能被其摘下，而次数肯定是 \(0\) 或 \(1\)。

那么非常直接的写出两点，如果员工 \(V_k\) 能够遇到苹果树 \(j\)，则：

  1. 点 \(F^e_j\) 在点 \(V_k\) 的子树内。
  2. 点 \(F^e_j\) 与点 \(V_k\) 的距离不超过 \(T_k - F^t_j\)。

一般子树判定我们选择 dfs 序判定方法，设 \(d_u\) 表示 \(u\) 的 dfs 序，\(s_u\) 表示 \(u\) 的子树大小，祖先关系的两点的距离，容易维护 \(D^T_u\) 表示点 \(u\) 到根的距离（区分大小写），于是可以写成如下形式：

  1. \(d_{V_k}\leq d_{F^e_j}\leq d_{V_k} + s_{V_k} - 1\)
  2. \(D^T_{F^e_j} - D^T_{V_k} \leq T_k - F^t_j\)

将式子 2 化成 \(D^T_{F^e_j} + F^t_j\leq T_k + D^T_{V_k}\)，不等式两边分别只与 \(j, k\) 有关，用二维数点即可。

\(V_k\) 是环上的点

考虑记 \(L^e_j\) 表示苹果 \(j\) 从 \(F^e_j\) 不断走，最终第一次走到环上的点，类似的定义 \(L^t_j\) 表示第一次走到环上的时间，再从环上一点开始，沿出边走到点 \(u\) 的距离记为 \(D^C_u\)，容易发现最终答案不与这一点的选择有关。

记 \(m\) 为在 \(V_k\) 所在的内向基环树中的苹果数量，再记 \(L_C\) 为所在环的环长，列式计算答案：

\[\overset{m}{\underset{i=1}{\sum}} \max(0, \Big\lfloor{\frac{T_k - (L^t_i + D^C_{V_k} - D^C_{L^e_i} + L_C\times [D^C_{V_k} < D^C_{L^e_i}])}{L_C}}\Big\rfloor +1) \]

先化个简：

\[\overset{m}{\underset{i=1}{\sum}} \max(0, \Big\lfloor{\frac{T_k - (L^t_i + D^C_{V_k} - D^C_{L^e_i})}{L_C}}\Big\rfloor +[D^C_{V_k}\ge D^C_{L^e_i}]) \]

这个式子看起来非常难以处理，考虑先强制认为全体都成立 \(D^C_{V_k}\ge D^C_{L^e_i}\)，此时式子变为：

\[\overset{m}{\underset{i=1}{\sum}} \max(0, \Big\lfloor{\frac{(T_k - D^C_{V_k}) - (L^t_i - D^C_{L^e_i})}{L_C}}\Big\rfloor +1) \]

换元 \(X_k = T_k - D^C_{V_k}, Y_i = L^t_i - D^C_{L^e_i}\)，注意 \(X_k\) 仅跟询问有关，\(Y_i\) 则仅跟苹果树有关，则可以简化：

\[\overset{m}{\underset{i=1}{\sum}} \max(0, \Big\lfloor{\frac{X_k - Y_i}{L_C}}\Big\rfloor +1) \]

当 \(X_k < Y_i\) 时，显然一定取 \(0\)，当 \(X_k\ge Y_i\) 时，一定取后者，考虑用计算 \(X_k - Y_i\) 时的答案代替与 \(0\) 取 \(\max\)，改写这个式子：

\[\underset{Y_i\leq X_k}{\sum} \Big\lfloor{\frac{X_k}{L_C}}\Big\rfloor - \Big\lfloor{\frac{Y_i}{L_C}}\Big\rfloor + [(X_k\bmod L_C)\ge (Y_i\bmod L_C)] \]

也即：

\[S\Big\lfloor{\frac{X_k}{L_C}}\Big\rfloor - \Big(\underset{Y_i\leq X_k}{\sum} \Big\lfloor{\frac{Y_i}{L_C}}\Big\rfloor\Big) + \Big(\underset{Y_i\leq X_k}{\sum} [(X_k\bmod L_C)\ge (Y_i\bmod L_C)]\Big) \]

此时有第一个偏序，\(X_k\ge Y_i\)，询问与苹果树分别按照 \(X_k,Y_i\) 升序后双指针扫描，记录 \(S\) 的数量以及此时的 \(\Big\lfloor{\dfrac{Y_i}{L_C}}\Big\rfloor\) 的和，得以解决前两项。观察第三项，相当于是两个偏序关系，离散化 \((X_k\bmod L_C), (Y_i\bmod L_C)\) 后进行二维数点即可。

但是话又说回来了，这个答案对吗？不对，因为我们强制认为 \(D^C_{V_k}\ge D^C_{L^e_i}\) 是成立的，但总是有不成立的，这些不成立的需要强制 \(-1\)，那么不成立且需要 \(-1\) 的满足：

  • \(D^C_{V_k} < D^C_{L^e_i}\)
  • \(X_k\ge Y_i\)

观察到现在还是两个偏序关系，这倒是提醒我们了：可以继续二维数点。

对每个内向基环树分别做上述二维数点，于是本题就做完了，时间复杂度为 \(\mathcal{O}((N+M)\log_2 N + (M+Q)\log_2 M)\)。实现有难度，也有细节，注意负数除法的下取整以及取余数。

Question 2. 「JOISC 2024 Day1」滑雪 2

KOI 高地上有 \(N\) 个点，每个点有一个初始的海拔 \(H_i\)，初始有一个可用的连接设施，在点 \(i\) 增设一个连接设施的费用为 \(C_i\)，每个点可无限增设连接设施。

JOI 先生选择一个点，建设度假酒店，并且选择一些点对，建设单向滑道，使得每个点都能滑到酒店的所在点，具体的：

  • 执行若干次操作：选择一个点 \(i\)，花费 \(K\) 的代价，使得该点的海拔增加 \(1\)。
  • 选择一个点，建设度假酒店。
  • 执行若干次操作：选择一个点 \(i\)，花费 \(C_i\) 的代价，在该点增设一个连接设施。
  • 对建设度假酒店外的 \(N-1\) 个点，依次执行一次如下操作：
    • 设当前的点编号为 \(i\)，找到一个海拔严格低于点 \(i\) 的点 \(j\)，仅耗费点 \(j\) 的一个连接设施，建设一条从 \(i\) 到 \(j\) 的单向滑道。

完成建设目标的最小代价是多少？

\(N\leq 300\)

首先我们给出一些引理：

Lemma 1

一个点只要海拔被拔高了，那么就不会再选择在其上增设连接设施。

证明：不妨设 \(x\) 点海拔被抬高，点 \(x\) 连向点 \(y\)，同时点 \(a,b\) 均连向点 \(x\)，显然拔高前 \(H_x < H_y\)，否则没有抬高的必要。

若 \(C_x < C_y\)，则无需抬高，将 \(y\) 指向点 \(x\)，同时将 \(a,b\) 中任意一个改向点 \(y\)；否则，将 \(a,b\) 中任意一个改向点 \(y\)，都是最优的。

Lemma 2

每个高度中 \(C_i\) 最小的点会保留在原高度。

证明：显然每个高度至少要保留一个点，否则大规模下移不劣。考察需要继续上抬海拔的点，这些点的 \(C_i\) 一定是比较大的（因为 \(C_i\) 小的留下来了），相比之下，该高度下 \(C_i\) 最小的点可能代价会更小。

Algorithm

于是设计 DP，不妨设 \(f_{i,j,k}\) 表示当前考虑到了高度 \(i\)，剩下了 \(j\) 个可用的连接设施，当前有 \(k\) 个点要继续抬升海拔。

转移考虑 \(i\to i+1\)，枚举一个 \(u\) 表示使用原来的 \(u\) 个可用的连接设施，同时新增 \(u\) 个可用的连接设施，枚举一个 \(v\) 表示新增 \(v\) 个可用的连接设施，显然会建在海拔不超过 \(i\) 的所有点中 \(C_i\) 最小的那一个（显然它会是某个高度中 \(C_i\) 的最小值，于是它会被保留）。

不妨设 \(M_i\) 表示海拔不超过 \(i\) 的所有点中 \(C_i\) 的最小值，设 \(T_i\) 表示海拔为 \(i\) 初始有多少个点，写出转移式：

\[f_{i,j,k} + K\times k + v\times M_i\to f_{i+1,j+v,k+T_{i+1} - u-v} \]

时间复杂度为 \(\mathcal{O}(N^4(N+H_{\max}))\)。

Lemma 3

每个高度上所有新增的点一定尽可能用完先前高度的所有连接设施。

证明：因为每个新增的点会带来一个新的可用的连接设施，可以给之后的点使用。

Optimization 1

于是只需要令 \(u=\min(j, k+T_{i+1})\)，省去一个转移，时间复杂度为 \(\mathcal{O}(N^3(N+H_{\max}))\)。

Optimization 2

我们不妨换一种形式来看这个转移式，初始我们只转移 \(v=0\) 的情况，而后每次可以让 \(v\) 扩大 \(1\) 的时候再增加 \(M_i\) 的代价。

此时这个 \(v\) 就像物品的体积一样，做类似完全背包，为了满足上述转移的要求，升序枚举 \(j\) 且倒序枚举 \(k\) 即可。

写一下转移式子：

\[f_{i,j,k} + K\times k \to f_{i+1,j,k+T_{i+1} - u} \]

与

\[f_{i+1,j, k+T_{i+1}-u} + M_i \to f_{i+1,j+1,k+T_{i+1} - u-1} \]

上述转移顺序就是为了可以在更新 \(v\) 加上一的状态后依旧可以枚举到它，从而完成 \(v\) 不断加一的过程。

时间复杂度为 \(\mathcal{O}(N^2(N+H_{\max}))\)。

Lemma 4

并非每个高度都有用，仅需要考虑所有点依次排开到每个高度 \(1\) 个点就可以。

证明：因为这些高度对应着仅仅增加海拔，而不增加任何一个连接设施，就是成为接近链的状态。新建连接设施，根据上述引理，它会回到原海拔，所以这些高度就足够。

Optimization 3

离散化这些高度后继续 DP 即可，时间复杂度为 \(\mathcal{O}(N^3)\)。

注意中间计算代价可能会超过 long long 存储极限，但是显然可以做到不超过 long long 极限，所以此时强制取 \(\min\) 即可。

Question 3. [QOJ8351] Ruin the legend

给定长度为 \(n\) 的单调增正整数序列 \(a\) 与一正整数 \(k\)，请求出有多少个排列 \(p\) 满足 \(\forall 1\leq i < n, |a_{p_i} - a_{p_{i+1}}|\ne k\)，答案对 \(P = 998244353\) 取余。

\(n\leq 5000, k\leq 10^6, a_i\leq 10^9\)

首先取出 \(a\) 中所有的极长的公差为 \(k\) 的等差子序列，显然这个限制只在每个子序列内有效而各子序列独立。

这个问题同时等价于重排序列 \(a\)，考虑将重排后的序列记为 \(b\)，同时将 \(b\) 中相邻两个差 \(k\) 的数进行合并为一段，考虑 DP，设 \(f_k\) 表示最终 \(b\) 的段数为 \(k\) 的方案数。

于是可以对着每个等差子序列分别做然后背包合并。

假设在每个等差子序列内做这个问题，设 \(g_{i,j,0/1}\) 表示考虑到子序列内的第 \(i\) 个数，有 \(j\) 个段，当前段长度是否 \(>1\)，因为 \(> 1\) 的段可以翻转。

\[\begin{aligned} g_{i,j,0} = g_{i-1,j-1,0} + g_{i-1,j-1,1}\\ g_{i,j,1} = 2g_{i-1,j,0} + g_{i-1,j,1}\\ \end{aligned} \]

翻转的 \(2\) 倍在开启一段长度 \(> 1\) 的段时计算，时间复杂度为 \(\mathcal{O}(n^2)\)。

考虑计算答案，显然分成段数为 \(k\) 中的 \(k\) 个段可以随意调换顺序，所以最终答案为 \(\sum_{1\leq i\leq n} (-1)^{n-i} f_i i!\)。

Question 4. 「JOI Open 2025」冒泡排序机

给定一个长度为 \(N\) 的正整数序列 \(A\)，有 \(Q\) 个操作，分两种类型：

  • 1，对序列 \(A\) 执行一次冒泡：
    • 称一次冒泡为：依次取 \(i=1,2,\cdots, N-1\)，若 \(A_i > A_{i+1}\)，则交换 \(A_i, A_{i+1}\) 的值。
  • 2 l r，求当前序列 \(A\) 中下标在 \([l,r]\) 范围内的元素之和。

\(N,Q\leq 5\times 10^5, A_i\leq 10^9\)

首先将询问差分成 \([1,r] - [1,l-1]\) 的形式，考虑刻画 \(k\) 次冒泡之后长度为 \(p\) 的前缀中的元素有哪些。

  1. 位于位置 \(p\) 之后的元素，最多向左移动 \(k\) 次（每次冒泡移动 \(1\) 个位置），故仅需考虑区间 \([1,p+k]\) 中的元素。
  2. 冒泡之后小的元素在前面，故是该区间内的前 \(p\) 小。
  3. 注意 \(p+k\) 和 \(n\) 需要取 \(\min\)。

所以询问相当于是求前缀前 \(k\) 小数的和的形式，主席树即可，时间复杂度为 \(\mathcal{O}((N+Q)\log_2 N)\)。

Question 5. [ICPC Seoul Regional 2023] A. Apricot Seeds

给定一个长度为 \(n\) 的非负整数序列 \(b\)，给出 \(q\) 次询问，每次询问给出 \((l,r,k,x,y)\)，求：

  • 设 \(a\) 为 \(b\) 中下标在 \([l,r]\) 范围内的子序列，下标重编号为 \(1\sim r-l+1\)，对 \(a\) 执行 \(k\) 次冒泡，求 \(a\) 中下标在 \([x,y]\) 范围内的元素之和。

\(n\leq 10^6, q\leq 5\times 10^5, k\leq r-l\)

类比前一个问题，依旧是差分询问，主席树改成区间前 \(k\) 小数的和。

具体的，假设要求 \(a\) 中长度为 \(p\) 的前缀，相当于是区间 \([l,\min(l+p+k-1,r)]\) 内的前 \(p\) 小数之和。

时间复杂度为 \(\mathcal{O}((n+q)\log_2 n)\)。

Question 6. [Petrozavodsk Winter 2021. Day 9. Grand Prix of Suwon] A. Another Tree Queries Problem

给定一棵 \(N\) 个节点的树，每个节点的点权 \(A_i\) 初始为 \(0\)，维护 \(Q\) 个操作，有三种类型：

  • 1 u v，表示将根节点置为 \(u\)，然后将 \(v\) 子树内的所有节点的点权加上 \(1\)。
  • 2 u v，表示将 \(u\) 到 \(v\) 路径上的所有节点的点权加上 \(1\)。
  • 3 v，设 \(d(x,y)\) 表示树上 \(x,y\) 两点间的边数，求 \(\sum_{1\leq i\leq n} d(v,i)\times A_i\) 的值。

\(N,Q\leq 2\times 10^5\)

首先考虑刻画操作 \(3\) 的式子，我们可以用一种有意思的方法来刻画，考虑在如下树中计算 \(v = 2\) 时的答案：

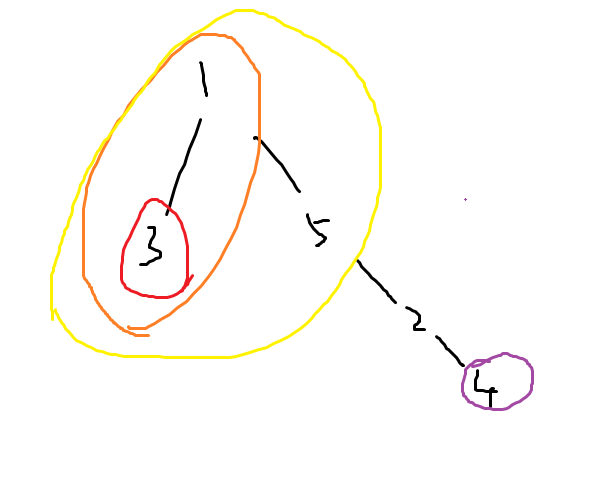
sample

每个颜色的圈中的点的点权求和，然后将各个圈的点权和求和，得到原答案。

这可以启发我们，答案由两部分组成，将根节点置为 \(1\)，设 \(c(u)\) 表示 \(u\) 到 \(1\) 的路径上的点的点集，设 \(S(u)\) 表示 \(u\) 子树内所有节点的点权的和：

  • 若 \(v\notin c(u)\)，则对答案的贡献为 \(S(v)\)。
  • 若 \(v\in c(u)\) 且 \(v\ne u\)，则对答案的贡献为 \(S(1) - S(w)\)，其中 \(w\) 为 \(v\) 在 \(c(u)\) 上向 \(u\) 走一步后到达的点。
    • 那么我们可以在下面一个点统计答案，于是若 \(v\in c(u)\) 且 \(v\ne 1\)，则对答案的贡献为 \(S(1) - S(v)\)。
    • 那么我们还可以加上 \(S(1) - S(1) = 0\)，于是 \(v\ne 1\) 的限制可以消除，这将方便我们处理。

令 \(dep(u)\) 表示节点 \(u\) 的深度，\(sz(x)\) 表示以 \(1\) 为根时以 \(x\) 为根的子树大小，\(f(x)\) 表示以 \(1\) 为根时 \(x\) 的父亲节点的编号（\(f(1) = 0\)），则直接写下答案的式子：

\[\sum_{u\notin c(v)} S(u) + dep(v)S(1) - \sum_{u\in c(v)} S(u) \\ \]

我们可以将其变形为：

\[\sum_{1\leq u\leq n} S(u) + dep(v)S(1) - 2\sum_{u\in c(v)} S(u) \\ \]

现在我们的目标转为维护 \(S(u)\) 的值，再来观察两个操作，先看操作 2 u v，它带来的影响是什么？不妨设 \(l\) 为节点 \(u,v\) 的最近公共祖先，于是点 \(u\) 的 \(S(u)\) 加上 \(1\)，点 \(u\) 的父亲 \(f(u)\) 的 \(S(f(u))\) 加上 \(2\)，以此类推，将 \(u\) 到 \(l\) 路径上不包括 \(l\) 的点 \(x\) 的 \(S(x)\) 顺次加上 \(1,2,3,\cdots,dep(u) - dep(l)\)；对 \(v\) 类似，将 \(v\) 到 \(l\) 路径上不包括 \(l\) 的点 \(y\) 的 \(S(y)\) 顺次加上 \(1,2,3,\cdots,dep(v) - dep(l)\)，然后对 \(c(l)\) 内的所有点 \(z\)，其 \(S(z)\) 加上 \(u,v\) 路径上的点的数量（容易计算得到为 \(dep(u) + dep(v) - 2\times dep(l) + 1\)）。

  • 这里有一个等差数列加，怎么维护？显然可以用差分前缀和大力拆式子，但是注意 \(dep\) 可以视作公差为 \(1\) 的等差数列，于是加等差数列等价于加 \(dep(u) + 1 - dep(x)\)。

再来看操作 1 u v，它带来的影响又是什么？这里分情况讨论：

  • 若 \(u=v\)，则每个点 \(x\) 的 \(S(x)\) 都加上 \(sz(x)\)。
  • 若 \(u\) 不在 \(v\) 的子树中，则 \(v\) 子树中的每个点 \(w\) 的 \(S(w)\) 都加上 \(sz(w)\)，但是对 \(c(v)\) 中的点 \(w\)，其 \(S(w)\) 都只会增加 \(sz(v)\)。
  • 若 \(u\) 在 \(v\) 的子树中，则此时 \(v\) 的子树与原本不一致，考虑记 \(w\) 为 \(c(u)\) 中唯一满足 \(f(w) = v\) 的点，则有：
    • 若节点 \(x\) 在 \(w\) 的子树中，则操作对 \(x\) 无影响。
    • 若节点 \(x\) 在 \(c(v)\) 上，由于挖去了 \(w\) 为根的子树，所以加上 \(sz(x) - sz(w)\)。
    • 若节点 \(x\) 不满足上述两种情况，则 \(w\) 为根的子树被挖去对 \(x\) 无影响，依旧加上 \(sz(x)\) 即可。

直接暴力维护，一点细节，时间复杂度为 \(\mathcal{O}(QN)\)。

可以发现 \(S(x) = A + B\times dep(x) + C\times sz(x)\)，维护 \(A,B,C\) 三个系数就可以维护 \(S(x)\) 以及若干 \(S(x)\) 的和，于是加入树剖维护，时间复杂度为 \(\mathcal{O}(Q\log_2 ^2 N)\)。

具体的，维护区间中点的数量，深度总和，子树大小总和，以及 \(S(x)\) 的和，对三个系数分别维护 tag 记录。涉及路径加、子树加、路径求和、单点求值。

Question 7. [Petrozavodsk Summer 2020. Day 4. Xi Lin Contest 6] L. Tokens on the Tree

给定一棵 \(n\) 个节点的树，树上每个点上可以有一个黑色棋子、或者一个白色棋子、或者没有棋子，按照如下方式定义 \(f(w,b)\)：

  • 树上恰好有总计 \(w\) 个白色棋子与 \(b\) 个黑色棋子。
  • 黑色棋子与白色棋子分别组成一个连通块。
  • 我们称两种状态等价当且仅当你可以通过如下的操作将一种状态变为另一种状态：
    • 将一个棋子移动沿着一条边移动一步，需要保证在此之后两种颜色的棋子依旧是一个连通块。
  • 定义 \(f(w,b)\) 为本质不同的状态数量，我们称两个状态本质不同当且仅当它们不等价。

多测。

\(\sum n\leq 2\times 10^5\)

先考虑 \(f(w,b)\) 如何求值，不失一般性，假定 \(w\ge b\)。

是否有一些节点必须要放置白棋？考虑一个节点 \(u\)，把 \(u\) 断掉后产生若干个连通块，假设没有任何一个连通块的大小达到 \(w\)，那么让白棋占据 \(u\)，现在白棋卡住了，剩下的连通块中，如果存在一个大小 \(\ge b\)，将黑棋全部放在该连通块内，就能够产生 \(1\) 种等价类（黑棋出不去，白棋移不走），所以每有一个大小 \(\ge b\) 的连通块就能够产生一个等价类。如果不放置白棋，那么黑棋就能够在不同连通块内乱窜。

假设这些必须要放置白棋的节点构成集合 \(S\)，则当 \(S\) 不为空时就是把 \(S\) 中所有节点全部删去，大小 \(\ge b\) 的连通块数量。

考虑 \(S\) 为空的时候，如果存在一个节点 \(u\)，删去 \(u\) 后出现两个大小 \(\ge w\) 的连通块与一个大小 \(\ge b\) 的连通块（不与前两个相同），那么白棋永远可以缩在一个连通块内让黑棋乱窜，同时白棋也能够在两个连通块之间来回，于是此时 \(f(w,b) = 1\)。

反之，如果不存在，则我们声称 \(f(w,b) = 2\) 恒成立。考虑三种情况，首先显然因为 \(S\) 为空，所以每个节点被删去后都至少产生一个大小 \(\ge w\) 的连通块。

Case 1. 存在节点 \(u\) 使得删除 \(u\) 后出现一个大小 \(\ge w\) 和一个大小 \(\ge b\) 的连通块

删除 \(u\) 后，只存在一个大小 \(\ge w\) 的连通块 \(C_1\) 与一个大小 \(\ge b\) 的连通块 \(C_2\)，剩下的连通块大小 \(< w\)，以下两种情况：

  • 白棋缩在 \(C_1\) 中，黑棋在外面移动。
  • 白棋完全不在 \(C_1\) 中，黑棋缩在 \(C_1\) 里面。
    • 对于该情况，因为不存在一个大小 \(\ge w\) 的连通块，所以点 \(u\) 必须被占据，导致黑棋无法出来。
  • 黑棋要么“在外面”要么“在里面”。

Case 2. 所有节点 \(u\) 在删除 \(u\) 后都只出现一个大小 \(\ge w\) 的连通块

从 \(u\) 开始，不断向着它唯一的大小 \(\ge w\) 的那个连通块走，直至到达一条边 \(e\)，其中 \(e\) 两端的连通块大小均 \(\ge w\)。

此时记 \(e\) 的两端分别为 \(x,y\)，则将 \(x,y\) 删去后得到的连通块大小均 \(< b\)。

此时要么白棋在 \(x\) 一边，黑棋在 \(y\) 一边且一定占据点 \(y\)；要么白棋在 \(y\) 一边，黑棋在 \(x\) 一边且一定占据点 \(x\)。

根据上述结论，设计算法：

降序扫 \(w\)，使用并查集维护 \(S\)，使用线段树维护表达式 \(\sum b\times f(w,b)\) 的值，需要支持前缀加前缀求和。合并的时候只需要把原先的大小删除然后加入新的大小。对于 \(S\) 为空的时候，在其次大子树上挂本节点的更新信息，每次遇到这类信息就将使得 \(f(w,b) = 1\) 的 \(b_{\max}\) 改成该节点的第三大子树大小即可。

容易发现 \(f(w,b) = f(b,w)\)，钦定 \(w\ge b\) 然后再钦定 \(w > b\) 分别计算求和即可。

时间复杂度为 \(\mathcal{O}(n\log_2 n)\)。

Question 8. 「JOISC 2022 Day2」团队竞技

\(N\) 个人中选出 \(3\) 个人组队，每个人有自己的思考能力 \(A_i\)，代码能力 \(B_i\) 和运气 \(C_i\)，组队的要求是：

  • 在这 \(3\) 个人中每个人都有自己拿手的能力。换句话说，\(3\) 个人分别拥有 \(3\) 人中思考能力的最大值、代码能力的最大值和运气的最大值，并且另外 \(2\) 人无法达到该最大值。

选出 \(3\) 个人，最大化 \(3\) 人的思考能力的最大值、代码能力的最大值与运气的最大值的总和。

\(N\leq 1.5\times 10^5\)

考虑贪心，分别按照 \(A_i,B_i,C_i\) 给 \(N\) 个人排序，每次分别取出最大值的代表人，如果三个人互相不同，则说明已经找到答案。

否则，如果有一个人 \(i\) 同时取到多个项目的最大值，则 \(i\) 一定不会被选中，因为其无论与谁组队都会在多个项目上完成偏序。

堆维护即可，每次标记无法被选中的人弹出堆，时间复杂度为 \(\mathcal{O}(N\log_2 N)\)。

Question 9. [YsOI2023] Prüfer 序列

给定长度为 \(m\) 的正整数序列 \(a\)，且 \(a\) 中每个元素均在 \([1,n]\) 之间。

等概率选择 \(a\) 中一个长度为 \(n-2\) 的序列作为 prüfer 序列并以此生成树 \(T\)，对每个点 \(u(1\leq u\leq n-1)\) 询问点 \(u\) 到点 \(n\) 的期望距离，答案对 \(P = 10^9 + 7\) 取余。

\(n\leq 15, m\leq 2500\)，对于每个 \(n\) 有独立的 \(m\) 的上限。

考虑 prüfer 序列构建树后的形态，节点 \(n\) 就相当于是树根，于是相当于问每个点的期望深度，便不需要管最近公共祖先。

考虑 prüfer 序列构建树的过程：维护集合 \(S\) 表示当前的叶子节点的集合，维护集合 \(T\) 表示当前已经挂到树上的点的集合，每次扫到序列中的 \(a_i\)，将 \(S\) 中最小值 \(u\) 的父亲记为 \(a_i\)，把 \(u\) 从 \(S\) 中删除并且加入 \(T\)，至于 \(a_i\) 可能加入 \(S\) 也可能不加入 \(S\)。

现在考虑 DP，由于 \(S,T\) 的终态确定而始态未知，倒序进行 DP，设 \(f_{i,j,S,T}\) 表示当前考虑到 \(i\sim m\) 这一段，而两个集合的状态为 \((S,T)\)，算点 \(j\) 的答案的总和，而 \(g_{i,S,T}\) 表示当前考虑到 \(i\sim m\) 这一段，且两个集合的状态为 \((S,T)\) 的方案数。

DP 转移分两种：

  • 不使用 \(a_i\)，容易 \(f_{i,j,S,T}\gets f_{i+1,j,S,T}, g_{i,S,T}\gets g_{i+1,S,T}\)。
  • 使用 \(a_i\)，考虑枚举 \(i\) 开始的后缀时集合状态为 \((S,T)\)，设 \(u\) 为 \(S\) 中最小值，则记 \(S' = S\setminus \{u\}, T' = T\cup \{u\}, R = S' \cup {a_i}\)，那么：
    • \(g_{i,S,T}\gets g_{i+1,S',T'} + g_{i+1,R,T'}\)
    • 若 \(j\ne u\)，则 \(f_{i,j,S,T}\gets f_{i+1,j,S',T'} + f_{i+1,j,R,T'}\)；否则，相当于点 \(u\) 要挂到树上，则 \(f_{i,j,S,T}\gets (f_{i+1,a_i,S',T'} + g_{i+1,S',T'}) + (f_{i+1,a_i,R,T'} + g_{i+1,R,T'})\)。

而满足条件的 \((S,T)\) 有多少？显然 \(S\cap T = \varnothing\) 所以不超过 \(\mathcal{O}(3^n)\)，但是根据 prüfer 序列的性质有 \(S\) 占据 \(S\cup T\) 的一段中较大的若干值外加一个可能的单点（删去一个节点后立刻新增的可使用点），所以不超过 \(\mathcal{O}(2^nn^2m)\)，状压这些状态，即可做到 \(\mathcal{O}(2^nn^3m)\) 的复杂度。

最后我们需要一点优化，考虑 \(S\) 中最终一定会有一个 \(n\)，直接声明 \(S\) 中一定含一个 \(n\) 即可减少状态数，实测此时已经可以通过。

Question 10. [NAC 2022] I. Reset

有 \(n\) 个任务需要完成，但是现在只有 \(c\) 天时间来完成了，第 \(i\) 个任务初始需要 \(t_i\) 的时间完成，而经过一次“深度思考”后完成时间减少 \(d_i\) 天，一旦减少到 \(0\) 及以下则可以瞬间完成，在这 \(c\) 天时间里，可以对每个任务执行最多一次“深度思考”，或者直接完成一些任务。

\(c\) 天时间不一定足够，于是可以进行一次“重启循环”，这可以重新带来 \(c\) 天时间，但是代价呢？只有在最后一次“重启循环”之后的 \(c\) 天中才可以完成任务，前面只能进行“深度思考”。

当然，每一个循环中依旧只能对每个任务执行最多一次“深度思考”。

现在请问：为了完成所有任务，执行“重启循环”的最少次数是多少？

\(n\leq 2\times 10^5, c\leq 10^9, d_i\leq t_i\leq 10^9\)

容易感受出答案中存在的单调性，考虑二分答案，假设我们要检验 \(v\) 次“重启循环”是否可行。

拟定一个 \(c\) 行 \(v+1\) 列的表格（因为 \(v\) 次“重启循环”带来了 \(v+1\) 个这样的循环），其中每一列代表一个“循环”，考察我们有哪些任务必须要在最后一个循环中占据时间。

设 \(h_i = \lceil{\frac{t_i}{d_i}}\rceil\) 表示所需的循环的次数，如果 \(h_i > v\)，则在前面的 \(v\) 个循环中一定剩下 \(t^r_i = t_i - v\times d_i\) 天的工作量，对于每一个任务，一定还是选择先来一次“深度思考”，于是需要 \(x_i = \max(t^r_i - d_i, 0) + 1\) 天来完成。设这些任务的 \(x_i\) 的总和为 \(S\)，那么一定要满足 \(S\leq c\)，因为这些只能在最后一个循环中做。

如果 \(S\leq c\) 成立，则最后一个循环还剩下 \(c - S\) 天，从表格中的最后一列删去 \(S\) 个格子，剩下的任务一定会靠着“深度思考”干到最后，每个任务会在 \(y_i = \min(h_i, v)\) 个循环中进行“深度思考”，最多一次“深度思考”的限制相当于每个任务不能划去同一列的多个格子，按照从上到下、每行从左到右划去格子的顺序，由于 \(y_i\leq v\) 在一定不会有这样的情况发生，此时只需要格子数量足够即可。

容易在 \(\mathcal{O}(n)\) 时间复杂度内完成一轮 check，总时间复杂度为 \(\mathcal{O}(n\log_2 V)\)。

Question 11. [CF1718D] Permutation for Burenka

称一个数组是 pure 数组当且仅当该数组内所有值互不相同。

对 pure 数组 \(a\) 定义 \(\operatorname{argmax}(a)\) 表示 \(a\) 中最大值的下标。

称两个 pure 数组 \(a,b\) similar 当且仅当其长度相同，设其长度为 \(n\)，则 \(\forall 1\leq l\leq r\leq n, \operatorname{argmax}([a_l,a_{l+1},\cdots, a_{r-1}, a_r]) = \operatorname{argmax}([b_l,b_{l+1},\cdots, b_{r-1}, b_r])\)。

现在有一个长度为 \(n\) 的排列 \(p\) 与一个长度为 \(n\) 的正整数序列 \(a\)，其中 \(a\) 有 \(k(k\ge 2)\) 个满足 \(a_i = 0\) 的位置表示这些位置填数待定。

给出一个大小为 \(k-1\) 的集合 \(S\)，给出 \(q\) 个询问，每个询问给出 \(d_j\)，表示询问：

  • 设 \(S' = S\cup \{d_j\}\)。
  • 将 \(S'\) 中的 \(k\) 个元素填入 \(a\) 中的 \(k\) 个填数待定的位置。
  • 保证能够使得 \(a\) 为 pure 数组，请问能否使得 \(a,p\) similar？

\(\sum n,\sum q\leq 3\times 10^5\)

首先观察这个限制的本质是什么？递归的定义到最大值左右两个区间中，所以 \(a,b\) similar 相当于 \(a,b\) 拥有完全一致的笛卡尔树。

给 \(p\) 建立笛卡尔树，在这棵笛卡尔树上考虑数组 \(a\)，数组 \(a\) 最终合法当且仅当对于所有祖先-后代点对 \((u,v)\) 满足 \(a_u > a_v\)。

考虑用已知的点规定每个点的范围 \(a_i\in [L_i,R_i]\)，即 \(L_i\) 是子树中所有 \(a_i\) 的最大值然后 \(+1\)，而 \(R_i\) 是祖先中所有 \(a_i\) 的最小值 \(-1\)。

这样看起来很合理，但是如果我拿出 \(a_i = 0\) 的连通块阁下如何应对？在这样的连通块中，假设全部满足原 \(L_i,R_i\) 的限制，那么对于不满足的，可以尝试对一条边上的两个值进行交换，如同冒泡一样这样的交换总是能够停止。

于是就相当于询问：\(S'\) 中的每个元素能够恰好匹配 \(k\) 个区间。考察如下贪心算法：

  • 按照区间的 \(R_i\) 升序排序，每次取出合法的元素中最小的那一个。
  • 这样的取法一定不劣，可以为其子区间提供更多可选值。

现在我们希望通过 \(S\) 与区间的匹配状况，得知最终 \(d_j\) 的条件。依旧尝试使用上述贪心算法，如果找到一个区间 \([L_i,R_i]\) 没有可选值了，那么必须满足 \(d_j\leq R_i\)，否则 \(d_j\) 对解决这个区间无影响，如果还能找到第二个没有可选值的区间，那就绝对无解了。

同理，我们还能够找到一个 \(i\) 使得对 \(d\) 的限制为 \(d_j\geq L_i\)，那么我们就得知了 \(d_j\in [L,R]\)，结合原 \(a_i\) 在笛卡尔树上的合法性，以及区间匹配的合法性判定是否有解。

正确性证明参照Question 3. 绝地反击，直接摆出结论：

根据 Hall 定理我们可以按照如下方式判定，其中 \(I(P)\) 表示 \(P\) 能连到的点的区间：

  • 枚举一个区间 \([l,r]\)，找到所有满足 \(I(P_i)\subseteq [l,r]\) 的 \(P_i\)，数这样的 \(P_i\) 的数量 \(C\)，看一下 \(C\) 和 \(r-l+1\) 谁大就可以。

设 \(F(l,r)\) 表示上述的 \([l,r]\) 数出的 \(C\)，设 \(G(l,r) = F(l,r) - (r-l+1)\)，于是有：

  • \(G(l,r) > 1\) 时一定无解。
  • \(G(l,r) = 1\) 的所有区间的交集 \([L,R]\) 规定了 \(d\) 的范围，此时贪心算法会在 \(R\leq r\) 的 \(r\) 检测出来，所以在 \([L,R]\) 范围内加入 \(d_j\) 能够使得这些 \(G(l,r)\) 变为 \(0\)。

时间复杂度为 \(\mathcal{O}(\sum n\log_2 n + \sum q)\)。

Question 12. 「JOISC 2023 Day1」护照

有 \(N\) 座城市，城市 \(i\) 的护照使旅客准入编号在 \([L_i,R_i]\) 范围内的城市且满足 \(L_i\leq i\leq R_i\)。

一名旅客想要获得一些护照使得准入所有城市，为此他可以执行如下操作：

  • 获得他所在的城市的护照。
  • 然后去到一个他准入的城市中。

给出 \(Q\) 个询问，每个询问给出城市 \(X_j\)，表示询问如果初始旅客在城市 \(X_j\) 且没有一本护照（估计是本地人），最少获得多少城市的护照才能达成目标。

\(Q\leq N\leq 2\times 10^5\)

当前状态可以用 \((l,r)\) 来表示，表示说当前准入的城市的编号范围为 \([l,r]\)，每个状态向 \(\mathcal{O}(N)\) 个状态转移，转移就是图上 bfs，时间复杂度为 \(\mathcal{O}(QN^3)\)。

注意到一个性质，如果区间只向单边扩展，那么一定扩展到最远处。

修改状态，用 \((l,r)\) 来表示当前准入的城市的编号范围至少为 \([l,r]\)，考虑如下的连边方式：

  • 当 \(l = r = k\) 时，连向 \((L_k,R_k)\)，代价为 \(1\)。
  • 当 \(l < r\) 时：
    • 找到 \([l,r]\) 中 \(L_i\) 的最小值 \(p\)，连向 \((m,r)\)，代价为 \(1\)。
    • 找到 \([l,r]\) 中 \(R_i\) 的最大值 \(q\)，连向 \((l,m)\)，代价为 \(1\)。
    • 连向 \((l+1,r),(l,r-1)\)，代价为 \(0\)。

然后对每个点开始跑图上 01-bfs，时间复杂度为 \(\mathcal{O}(QN^2)\)，显然可以通过反向连边并从 \((1,N)\) 开始，时间复杂度为 \(\mathcal{O}(N^2 + Q)\)。

又注意到状态一定是区间，所以限制就相当于要能够到达城市 \(1\) 和城市 \(N\)。那么就可以反边从 \(1,N\) 分别跑最短路，距离为 \(D^L_i, D^R_i\)，线段树优化建图后可以在 \(\mathcal{O}(N\log_2^2 N)\) 复杂度内求解。

但是又有问题了，直接用 \(D^L_i + D^R_i\) 可能有问题，因为会有重复的一段，但一定有些点是对的，其余点可以向这个点中转，于是再把这些边加进去后跑多元最短路即可。

或者新开一个虚点，向 \(1\sim N\) 分别连代价为 \(D^L_i + D^R_i\) 的边后跑单源最短路，于是最终每个点的最短路就是答案。

时间复杂度为 \(\mathcal{O}(N\log_2^2 N)\)，如果开了比较多的虚点，注意连边往哪个点连以及每条边的方向是什么。

Question 13. 「JOISC 2015 Day2」建筑装饰 3

给定一个长度为 \(N-1\) 的序列 \(B\)，求有多少个长度为 \(N\) 的正整数序列 \(A\) 满足如下条件：

  • 从 \(A\) 中删去一个数，保持剩下的数的相对顺序，得到序列 \(B\)。
  • 存在长度为 \(N\) 的排列 \(P\)，使得 \(A\) 为 \(P\) 中以 \(P_i\) 结尾的最长上升子序列的长度。

\(N\leq 10^6, B_i\leq N\)

这里最难受的就是第二个条件，考虑用更加直观的方式刻画该条件。

显然 \(A_1 = 1\)，而 \(A_2 = 1/2\)，当 \(A_2 = 1\) 时 \(A_3 = 1/2\)，否则 \(A_3 = 1/2/3\)，以此类推。设 \(M_i\) 为 \(A\) 中前 \(i\) 个数中的最大值且 \(M_0 = 0\)，我们不妨猜测 \(1\leq A_i\leq M_{i-1} + 1\)，具体怎么证明这个条件充要？

  • 下证排列 \(P\) 的 LIS 数组 \(A\) 一定满足该条件：
    • 根据 LIS 的 DP 转移方程：\(A_i = \underset{j < i, P_j < P_i}{\max} A_j + 1\leq M_{i-1} + 1\)，故一定成立该条件。
  • 下证满足该条件的数组 \(A\) 一定能够对应至少一个排列 \(P\)：
    • 设 \(S_i\) 为满足 \(A_j = i\) 的 \(j\) 的集合，按照 \(v\) 从小到大枚举 \(S_v\)，每个 \(S_v\) 内从大到小枚举元素 \(x\)，则 \(P_x\) 取当前没有写入 \(P\) 的最小正整数。

综上本条件充要，可以用此计数。

但话又说回来，有了这个条件也不方便计数，考虑掏出压箱底的武器——分类讨论，设 \(M_i\) 为 \(B\) 中前 \(i\) 个数的最大值：

  • \(B_i\ge M_{i-1} + 3\)，由于我极限填写 \(M_{i-1} + 1\)，但是一定会缺少 \(M_{i-1} + 2\)，肯定无解。
  • \(B_i = M_{i-1} + 2\)，此时就要求在 \(i\) 前面补充一个 \(M_{i-1} + 1\)。
  • 其余等价于没有限制。

如果我要求补充的数字不是同一个，那肯定也无解，否则设该数为 \(x\)，找到最小的限制位置 \(p\)，最靠前的 \(x-1\) 的位置 \(q\)，则 \(x\) 只能填写在 \(q\sim p\) 之间，具体有没有 \(+1/-1\) 的细节留给读者。

为什么找到最靠前的 \(x-1\) 的位置 \(q\) 就可以？因为第一个不合法的数是 \(x\) 所以 \(1\sim (x-1)\) 一定合法。

否则，每个位置都可以填写 \(M_{i-1} + 1\) 种数，唯一的问题就是填写可能会重，考虑一个长度为 \(L\) 的 \(B\) 中由数字 \(y\) 构成的极长连续段，当且仅当在 \(L+1\) 个位置插入 \(y\) 的状态互相重复，所以要减去 \(L\) 个计重的状态，累加就相当于减去所有连续段的长度总和，也就是 \(N-1\)。

可以在 \(\mathcal{O}(N)\) 复杂度内完成检验与计算。

posted @ 2025-10-21 08:24  ydzr00000  阅读(23)  评论(0)    收藏  举报