2025.9.26 - 9.30

Question 1. 「JOISC 2022 Day2」复制粘贴 3

给定一个编辑器，你需要输入一个长度为 $N$ 的小写字母字符串 $S$，编辑器有一个显示区和一个剪贴板，操作有如下三种：

令 $X$ 为显示区实时的字符串，$Y$ 为剪贴板实时的字符串。初始 $X,Y$ 均为空串。

输入：花费 $A$ 的时间，在 $X$ 后追加任意字符 $c$。
全选剪切：花费 $B$ 的时间，将 $Y$ 置为 $X$ 后将 $X$ 清空。
粘贴：花费 $C$ 的时间，在 $X$ 后追加 $Y$。

$N\leq 2500$

注意到这个问题本质上就是不断做如下操作：

利用原来的 $Y$ 以及自己打的字符，打出一个新的 $Y$。

那么就可以大力 DP，设 $f_{l,r}$ 表示将 $X$ 变为 $S$ 下标 $[l,r]$ 范围内的子串需要的最小时间。

显然有初始值 $f_{p,p} = A$，以及不使用剪贴板的两种转移：

\[f_{l,r} \gets \min(A + f_{l+1,r}, f_{l,r-1} + A) \]

接下来考虑使用剪贴板，设 $g(l,r,p,q)$ 表示 $S_{[p,q]}$ 在 $S_{[l,r]}$ 中不重叠出现的次数。

\[f_{l,r} \gets \underset{l\leq p\leq q\leq r}{\min} f_{p,q} + B + g(l,r,p,q)\times C + (r-l + 1 - (q-p + 1)\times g(l,r,p,q))\times A \]

不妨钦定转移顺序为「倒序扫 $l$，对每个 $l$ 升序扫 $r$」，这样可以完成区间 DP 同样的工作，同时也可以钦定 $p = l$。

随便做一下，时间复杂度为 $\mathcal{O}(N^3)$，带一个小于 $1$ 的常数，可以通过 $N\leq 1000$。

考虑优化，考虑更换枚举顺序为：

考虑一个区间 $[l,r]$，以及把这个区间当作剪贴板使用 $k$ 次，找到最短的 $[p,r]$ 使得 $S_{[l,r]}$ 在 $S_{[p,r]}$ 中不重叠出现了 $k$ 次。

则转移变为：

\[f_{p,r} \gets f_{l,r} + B + k\times C + (r-p+1 - (r-l+1)\times k)\times A \]

转移复杂度为：每个 $[l,r]$ 带来的枚举量为 $\dfrac{r}{r-l+1}$，同一个 $r$ 带来的枚举量为 $\mathcal{O}(N\ln N)$，于是时间复杂度为 $\mathcal{O}(N^2\ln N)$。

转移复杂度就非常神奇的对了，接下来考虑对每个 $[l,r],k$ 找到最大的 $p$，设 $t = r-l+1, k = 1$，等价于我们需要找到最大的 $p$ 满足：

$p+t-1 < l$
$S_{[p,p+t-1]} = S_{[l,r]}$

即最后一次与之不重叠的出现的位置，$k$ 更大就继续往前面找。设 $\text{lcp}_{i,j}$ 表示从 $i,j$ 位置开始的两个后缀的最长公共前缀与 $|i-j|$ 的较小值（这样可以不交），尝试翻译上述条件：

$\text{lcp}_{p,l}\ge t$

容易 DP 求出这个 $\text{lcp}$：

如果 $S_i = S_j$，则转移 $\text{lcp}_{i,j}\gets \text{lcp}_{i+1,j+1} + 1$，然后与 $|i-j|$ 取 $\min$。
否则 $\text{lcp}_{i,j} = 0$。

记 $h_{l,t}$ 表示最大的 $p$ 使得 $\text{lcp}_{p,l} = t$，这是容易计算的，先直接填表然后取后缀最大值即可。

问题解决了，于是枚举 $l,r,k$ 暴力转移即可，时间复杂度见上文。

Tips

有时可以通过不等式放缩真正需要考虑的数据的数量级。

Question 2. 「CEOI2023」Brought Down the Grading Server?

评测机被黑客攻击了！现在所有的提交需要重测！

$N$ 个评测机将要评测 $T$ 个题目，每个评测机将要评测 $S$ 份提交，第 $i$ 个评测机的第 $j$ 份提交为题目 $A_{i,j}$ 的代码。

每一个评测机在第 $t$ 个时刻都可以评测该评测机中的第 $t$ 份提交。

受限于评测机的性能问题，对于任意一个问题 $q$ 和任意两个不同的时刻 $t_1,t_2$，时刻 $t_1$ 中问题 $q$ 被评测的提交数量与时刻 $t_2$ 中问题 $q$ 被评测的提交数量相差不超过 $1$。

你需要重新安排每个评测机评测 $S$ 份提交的顺序，使得满足限制条件。

$N,S,T\leq 10^5, NS\leq 5\times 10^5$，保证 $S$ 是 $2$ 的幂，可以证明有解。

不妨考虑 $S = 2$ 的问题，发挥惊人的注意力，考虑生成一张这样的图：

在最终的安排中，对每台评测机 $p$，其第一份提交为题目 $a$ 的代码而第二份提交为题目 $b$ 的代码，则从 $a\to b$ 连边。

那么这张图，一定有，每个点入度和出度相差不超过 $1$。

由这个性质，注意力再次发力，我们猜测这个跟欧拉路有关。

考虑将原来的 $A_{i,1}$ 与 $A_{i,2}$ 连边，如果最终找出的欧拉路是 $A_{i,1}\to A_{i,2}$，则不变；否则交换 $A_{i,1}$ 与 $A_{i,2}$。

但是这样可能会有一大堆度数为奇数的点，如果考虑增加一个超级源点，其与所有度数为奇数的点连边，首先可以简单证明度数为奇数的点有偶数个（用度数和，$2n$，奇偶性什么的），然后现在所有的点度数均为偶数，可以跑出欧拉回路，现在只考虑与超级源点无关的边，根据这些边的定向决定 $A_{i,1},A_{i,2}$ 的顺序。

由于每个度数为奇数的点在新图中一定有入度与出度相等，删去与超级源点的边，则一定满足入度与出度相差不超过 $1$，所以直接忽略与超级源点的边也是正确的。

现在考虑 $S>2$，不妨分治 $S$，从大区间 $[1,S]$ 考虑，设当前区间为 $[l,r]$，中点为 $m$，则：

将每个评测机中 $[l,m]$ 向 $[m+1,r]$ 的点对应连边。

然后类似的加入超级源点，我们可以得到一个方案，这个方案根据出入度限制，一定满足：左半边与右半边每道题目评测的总次数相差不超过 $1$！

所以我们得以递归的解决 $[l,m], [m+1,r]$ 两个子区间，如果存在某道题目在两个不同时刻评测次数差 $\ge 2$，则这两个时刻一定会被我们在某次分治分隔开，于是左右半边相差至少为 $2$ 了，不符合先前的结论，所以得以证明最终这么做下去一定满足：任意两个时刻每道题目的评测次数差不超过 $1$。

时间复杂度为 $\mathcal{O}((NS+T)\log_2 S)$。

实现起来比较有细节，例如清空啊，找反向边什么的，不建议初学欧拉回路后直接写这个题。

Question 3. [JSOI2018] 绝地反击

给定平面上一位于 $(0,0)$ 的母舰，以及平面上 $n$ 艘飞船的位置 $P_i(x_i,y_i)$，你需要在最短的时间内让这些飞船飞到以母舰为圆心的半径为 $R$ 的圆 $O$ 上，且两两之间的圆周上距离最大化。

换句话说，飞船需要飞到圆的内接正 $n$ 边形的 $n$ 个顶点上，你可以自由决定飞船所飞到的顶点以及 $n$ 边形的角度。

最小化最远的飞船到它所需要达到的目的地的距离，飞船可以视作质点，所以你只需要最小化最大直线距离。

$n\leq 200, R, |x_i|,|y_i|\leq 100$

首先看到这个最大值最小化就直接二分答案，设当前需要 check 的答案为 $r$，容易得知每艘飞船能够到达圆 $O$ 上的一段圆弧。

感受一下，如果每艘飞船都选择到达圆弧上而没有任何一个到达端点处，那么我显然能够降低 $r$。

所以我们可以得知：如果有飞船能够到达一段圆弧而非整个圆，则其中一定有一艘会到达圆弧的端点处。枚举这个端点，进而我们可以得知正 $n$ 边形每个顶点的位置，点列按照弧度依次编为 $Q$。

通过解三角形等各种手段，假设我们可以知道每个点最终能够到达 $Q$ 中一段区间中的目标点，令 $I(P_i)$ 表示原 $P_i$ 能够到达的目标点的区间。

现在就是这样的一个问题：

一张二分图左右部均有 $n$ 个点，每个左部点连接编号一段区间内的右部点，判定二分图是否存在完美匹配？

由 Hall 定理知，二分图有完美匹配的充要条件为 $\forall S\subseteq L, |N(S)|\ge S$，其中 $N(S)$ 为邻域大小，而 $L$ 为左部点集。

由于要考虑 $S$ 就只能纯粹的考虑子集，不妨考虑 $N(S)$，这些为一段区间的并，显然我们只要判定有没有 $|S| > |N(S)|$ 的情况，我们声明：只需要考虑并集为环上一段区间的 $N(S)$，证明：

设 $L_f([a,b])$ 表示所有满足可达区间均在 $[a,b]$ 范围内的所有左部点构成的点集，换句话说，就是只能到达 $[a,b]$ 范围内的左部点构成的集合。
假定存在两个区间 $[a,b],[c,d]$，现已知 $N([a,b]\cup [c,d])$ 不满足条件，即 $|L_f([a,b]\cup [c,d])| > (d-c+1)+(b-a+1)$，且 $[a,b],[c,d]$ 不交。
容易发现 $L_f([a,b])\cap L_f([c,d])$ 为空，因为这个条件强于 $[a,b],[c,d]$ 不交。
则 $|L_f([a,b])| + |L_f([c,d])| = |L_f([a,b]\cup [c,d])| > (d-c+1)+(b-a+1)$，由集合的大小等价于其两个并为全集的不交子集的大小之和。
由不交，显然 $|L_f([a,b])|$ 对应 $b-a+1$，$|L_f([c,d])|$ 对应 $d - c + 1$。
于是我们得到 $|L_f([a,b])| > b-a+1$ 或者 $|L_f([c,d])| > d-c+1$。

用人话说就是，两段不交区间的并不满足条件，由于这两个区间不交所以互不干涉，所以至少有其中一个区间不满足条件，所以我们只需要考虑环上并为一段区间。

当然，由于这些区间可能被裂开，所以我们只需要断环为链然后倍长，然后根据 Hall 定理我们可以按照如下方式判定：

枚举一个区间 $[l,r]$，找到所有满足 $I(P_i)\subseteq [l,r]$ 的 $P_i$，数这样的 $P_i$ 的数量 $C$，看一下 $C$ 和 $r-l+1$ 谁大就可以。

但是这太暴力了，但是感觉这个东西可以扫描线，我们对着 $r$ 升序扫描，则每次将所有右端点为 $r$ 的区间的左端点 $i$ 计数器 $v_i\gets v_i +1$，于是右端点 $r$ 合法当且仅当：

设 $l = r-n + 1$，不存在 $p\in [l,r] $ 使得 $v_p + v_{p+1} + \cdots + v_r > r-p+1$。
也即 $(v_p - 1) + (v_{p+1}-1) + \cdots + (v_r-1) > 0$。
含义就是框定 $[p,r]$ 的时候就可以在左端点处增加 $I(P_i)\subseteq [p,r]$ 的 $P_i$ 的数量，而不至于多算少算。

显然只考虑最大的后缀和，所以只需要求序列 $[v_l-1,v_{l+1}-1, \cdots, v_{r-1}-1,v_r-1]$ 的最大后缀和是否 $ >0$，线段树维护即可。

时间复杂度为 $\mathcal{O}(n^2\log_2 n\log_2 V)$，二分并选定端点后单次 $\mathcal{O}(n\log_2 n)$。

运用网络流或者在扫描线处暴力，时间复杂度为 $\mathcal{O}(n^{3.5}\log_2 V)$ 与 $\mathcal{O}(n^3\log_2 V)$，后者可以通过。

call back: “通过解三角形等各种手段”找区间？

这一段才是本题的实现难点~~，线段树在这里有什么难的~~。

以下请自行画图辅助理解，默认读者了解解三角形以及简单的综合性初中几何。

首先，判定一个点 $P$ 是否能够到达整个圆，假设点 $P$ 到圆点的距离为 $d$，当前要 check 的答案是 $r$，显然我只要能够到达距离 $P$ 最远的圆上的点即可。

根据几何原理，作线段 $PO$ 并延长，$PO$ 的延长线交圆与点 $Q$，容易得知 $|PQ| = R + d$ 是最大的，于是只要 $r\ge R+d$ 就可以到达整个圆上。

其次，判定点 $P$ 与圆的两个交点的位置，显然我们可以只考虑这个位置的极角（一个点 $A$ 的极角的定义为：从 $O$ 点向 $x$ 轴正半轴引射线，逆时针旋转角度 $\theta$ 后射线过点 $A$，则极角为 $\theta$）。

假设两个交点分别为 $A,B$，全等易证 $A,B$ 关于直线 $OP$ 对称，设 $\angle AOP = \alpha$，已知 $OA = R, OP = d, AP = r$。
$\cos \alpha = \dfrac{R^2 + d^2 - r^2}{2Rd}$。
设点 $P$ 极角为 $\beta$，容易得知 $\beta-\alpha, \beta + \alpha$ 分别为点 $A,B$ 的极角。

最后，如何找出范围？

如果能够到达整个圆，则 $L_i = 1, R_i = n$。
否则，设指定端点的极角为 $\gamma$，生成以该极角为一顶点的正 $n$ 边形的所有顶点的极角构成的序列 $T$，为了倍长再生成 $+2\pi$ 之后一圈。
直接用 $\beta - \alpha, \beta + \alpha$ 在 $T$ 中二分求得 $L_i,R_i$。

不要忘记选用适合的 $\epsilon$（即 eps），本人取 $\epsilon = 10^{-9}$。

Tips

设正整数 $x,y$，则 $x+y$ 在第 $d$ 位进位，当且仅当：
- $a = x\bmod 10^{d+1}, b = y\bmod 10^{d+1}, a+b\ge 10^{d+1}$。
换元与轮换对称式的对称性。
加数操作的转化。

Question 4. [ARC158] D. Equation

给出正整数 $n$ 和素数 $p$，求一组 $(x,y,z)$ 满足：

$1\leq x < y < z\leq p-1$
$(x+y+z)(x^n+y^n+z^n)(x^{2n}+y^{2n}+z^{2n}) \equiv x^{3n} + y^{3n} + z^{3n}\pmod p$

多测。

$T\leq 10^5, n,p\leq 10^9$

设 $F(x,y,z)$ 为等号左边的式子，设 $G(x,y,z)$ 为等号右边的式子。

注意到等式两侧都是齐次式，设一正整数 $t$，则有 $F(x,y,z) = t^{3n+1} F(x/t,y/t,z/t), G(x,y,z) = t^{3n} G(x/t,y/t,z/t)$。

假设我们得到了一组 $(x,y,z)$ 满足 $tF(x,y,z) = G(x,y,z)$，那么取 $t = G(x,y,z)\times F^{-1}(x,y,z)$，根据上述引理，知 $(xt,yt,zt)$ 是一组解。

这样我们将要求 $F(x,y,z) = G(x,y,z)$ 转变为了 $F(x,y,z), G(x,y,z)$ 均不为 $0$。

感性猜测一下这样的 $(x,y,z)$ 占比不小，随机 roll 到合法为止，可以通过。

Question 5. 「The 3rd Ucup Stage 29: Metropolis」K. Knights of Night

现有两组骑士，第一组骑士有 $n$ 人，第 $i$ 人的力量是 $a_i$；第二组骑士也有 $n$ 人，第 $j$ 人的力量是 $b_j$。

让第一组的第 $i$ 名骑士和第二组的第 $j$ 名骑士进行一次战斗，战斗的疯狂度是 $(a_i + b_j)\bmod P$，其中 $P = 998244353$。

有 $m$ 对骑士之间不能组织决斗，你需要对 $x = 1,2,\cdots, k$ 求出：

组织 $x$ 对不同的骑士（每一名骑士可以多次参与战斗，但该骑士对另一组每一名骑士的战斗只能组织一次）战斗，所有战斗的疯狂度的总和最大是多少？
如果组织不出，请告知。

$n\leq 10^5, m\leq 3\times 10^5, k\leq \min(n,200)$

容易发现这个是最大费用最大流的模板题，只要我们能把图建出来，显然这么多边建不出来。

显然可以得出两个引理，假设要匹配 $k$ 场战斗：

对于第一组的每一名骑士，只需要保留最大的 $k$ 场战斗。
对于第二组的每一名骑士，只需要保留最大的 $k$ 场战斗。

不太显然的是，上面两个引理得出的战斗可以取交集，证明：

假设得出了第一组战斗的所有边，其中第二组中有一名骑士 $x$ 有 $ > k$ 条边，再假设第 $(k+1)$ 大的边 $e_1$ 在匹配中。
显然此时前 $k$ 大的边中有一条边 $e_0$ 没有被匹配，令 $e_0$ 与第一组的骑士 $y$ 相连，此时 $y$ 一定匹配了 $k$ 条边，否则直接把 $e_0$ 连上并把 $e_1$ 断掉更优。
显然 $e_0$ 会是骑士 $y$ 中的前 $k$ 大的边，不妨设骑士 $y$ 的那条不在前 $k$ 大中的匹配边为 $e_2$，断 $e_2$ 连 $e_0$ 即可。

所以总是能够调整得到，所以可以取交集，使用 nth_element 可以完成找出这 $\mathcal{O}(nk)$ 条边。

再给出一个引理：只需要保留这些边中边权最大的 $(2k-1)(k-1)+1$ 条边就可以匹配 $k$ 场，证明：

假设一个第一组的骑士 $u$ 与第二组的骑士 $v$ 完成匹配，那么极限 $u,v$ 同时阻断另一组与之连接的全体连边，加上自己的匹配边，共 $k-1 + k-1 + 1 = 2k-1$ 条边被声明不可用。
假设前 $(k-1)$ 对骑士的匹配都如此，于是消耗掉 $(2k-1)(k-1)$ 条边。
再加上一条边，此时这条边一定可以匹配上。

综上，在这张点数 $\mathcal{O}(n)$，边数 $\mathcal{O}(k^2)$ 的网络流中跑最大费用最大流即可，每次 $+1$ 的总流量看能不能增加最大流，若增加报出此时费用即可，否则无解。

选择经典款的费用流算法，可以通过。

Question 6. 「The 3rd Ucup Stage 29: Metropolis」H. Hexagon Puzzle

在一个大小为 $n$ 的六边形格子（下图展示 $n = 3$）上摆积木（下图展示 $6$ 种积木），最多能摆多少？给出方案。

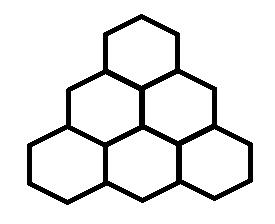
chessboard

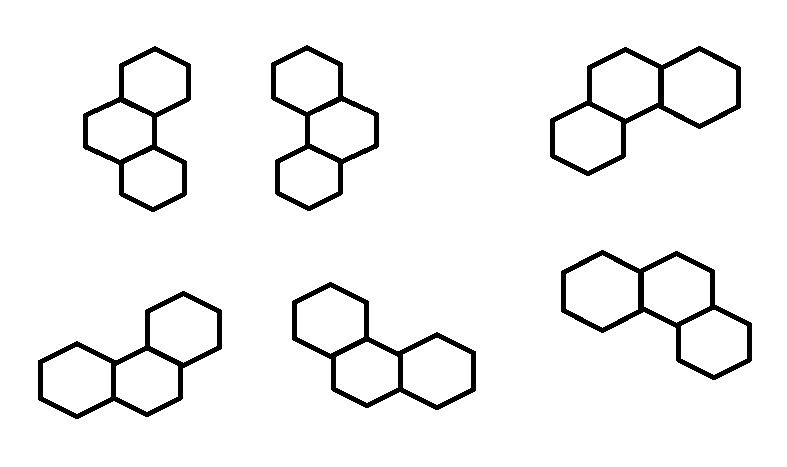
block

要求如下：

积木之间不能重叠。
积木要完全放在六边形格子内部。

同时你需要为相邻的积木块选用不同的大写字母进行标识。

$n\leq 1024$

从 $n$ 开始，将底下的三行填完，规约到 $n - 3$ 的情况，最后一行的左右顶点战略性放弃。

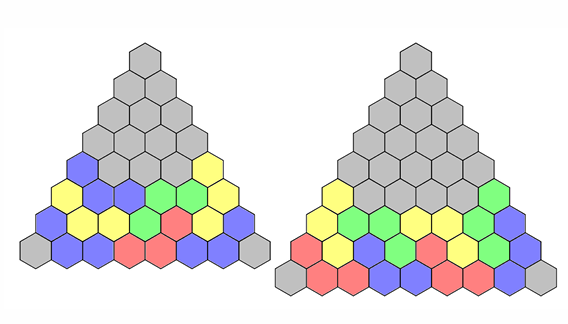
transform

对 $n$ 的奇偶性分别讨论出一种摆放方案即可，上述图片已经大致给出了偶数与奇数的方案。

容易标识不同的大写字母，毕竟一个积木只有 $14$ 条邻边，随便标一下就可以了。

时间复杂度为 $\mathcal{O}(n^2)$，与输出同阶。

Question 7. 「The 3rd Ucup Stage 29: Metropolis」J. Just-in-Time Render Analysis

给出 $n$ 个矩形，称一个矩形的深度为完全包含这个矩形的矩形数量，现在 $n$ 个矩形都是未激活状态，维护 $q$ 个操作：

^ x，改变矩形 $x$ 的状态，即激活与未激活之间的转换。
? k，求所有深度为 $k$ 的矩形中，其包含至少一个（包括它自己）激活的矩形的矩形数量。

$n,q\leq 5\times 10^5$，保证任意两个矩形之间不会有交点。

首先这个矩形关系看起来就很能建树。

Step 1. 矩形关系如何建树？

按照 $x$ 坐标升序扫描线，将每个矩形的上边界，下边界插入 set，每次遇到一个矩形的左边界要加入矩形的时候，二分上边界的上放最靠近该边界的 $y$ 坐标：

如果这个 $y$ 坐标对应上边界，则其下边界一定在新增矩形下边界下方，故该矩形的“父亲节点”为这个 $y$ 坐标对应的矩形。
反之对应下边界，则新增矩形与该下边界对应的矩形会被同一个矩形包含，两个矩形的“父亲节点”相同。

于是我们可以建树，为了方便，称坐标系平面为 $0$ 号矩形，其为根，深度为 $0$。

~~才不是因为不会这个 WA 了 12 发才写这题的总结呢！~~

Step 2. 建树后又如何？

先翻译操作：

^ x，单点修改 $v_i\in \{0,1\}$，其中 $0\to 1, 1\to 0$。
? k，询问有多少个深度为 $k$ 的节点，其子树 $v_i$ 和不为 $0$。

那么显然可以做类似前缀和/差分的操作，把单点修改改为根链（从根到该节点的链）上所有点的 $s_i$ 进行 $+1/-1$，而询问就相当于问有多少个指定深度的点 $s_i$ 不为 $0$。

考虑每次修改带来的影响，不考虑每个点变为几，仅考虑有哪些点的 $s_i$ 从 $0$ 变为 $1$，就相当于把这个点加入点集 $T$ 后包含 $T$ 中所有点的最小连通块的变化。

根据寻宝游戏的 Trick，容易知道只需要考虑新增点 $u$ 的 dfs 序在原 $T$ 中 dfs 序的前驱与后继的对应点，两个点分别与 $u$ 求得 LCA 后取深度较大的，记为 $v$，则 $u\to v$ 就是新增的点所对应的路径（不含 $v$），显然此时深度是一段连续的区间，综合我们的询问，可以使用树状数组完成。

时间复杂度为 $\mathcal{O}((n+q)\log_2 n)$。

posted @ 2025-09-27 16:26 ydzr00000 阅读(12) 评论(0) 收藏举报

刷新页面返回顶部

ydzr00000

2025.9.26 - 9.30

Question 1. 「JOISC 2022 Day2」复制粘贴 3

Tips

Question 2. 「CEOI2023」Brought Down the Grading Server?

Question 3. [JSOI2018] 绝地反击

call back: “通过解三角形等各种手段”找区间？

Tips

Question 4. [ARC158] D. Equation

Question 5. 「The 3rd Ucup Stage 29: Metropolis」K. Knights of Night

Question 6. 「The 3rd Ucup Stage 29: Metropolis」H. Hexagon Puzzle

Question 7. 「The 3rd Ucup Stage 29: Metropolis」J. Just-in-Time Render Analysis

Step 1. 矩形关系如何建树？

Step 2. 建树后又如何？

公告