透视投影理解
透视投影以视锥体为核心，将视锥体的点对应到\((-1,-1,-1) - (1,1,1)\)的立方体盒，\(视锥体 \to 裁剪坐标系\)。
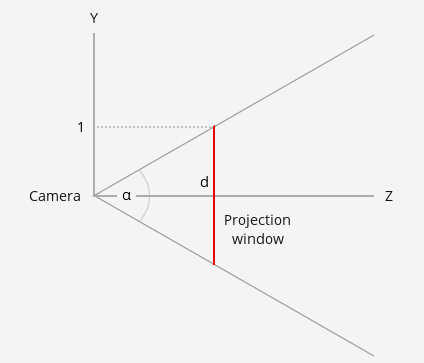
1. 投影面
\(d\)
高为\(2\)，垂直于\(z\)轴的平面，距原点的距离为
\[\frac1d = tan(\frac{\alpha}2) \Rightarrow d=\frac1{tan(\frac{\alpha}2)}=cot(\frac{\alpha}2)
\]
\((x_d, y_d)\)
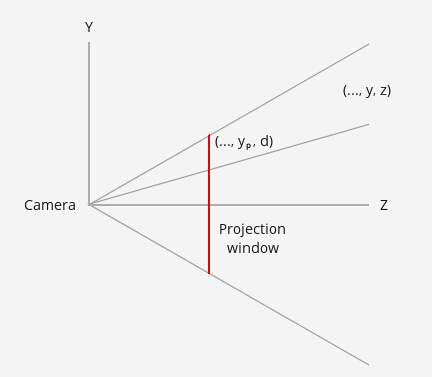
任意点\(P\) 点投影到投影平面，其投影关系为：
\[\frac{y_d}d=\frac yz \Rightarrow y_d = \frac {y\cdot d}z = \frac {y\cdot cot(\frac{\alpha}2)}z
\]
同理，
\[x_d = \frac {x\cdot cot(\frac{\alpha}2)}z
\]
由于投影面\(XY\)存在宽高比 \(ar=\frac WH\)，视锥体内\(x_d\) 还需要变换到\([-1,1]\)内，
\[x_{da} = \frac{x_d}{ar}
\]
\((x_{da}, y_d)\)齐次化
用齐次坐标表示上述\((x_{da},y_d)\)坐标为
\[\begin{pmatrix}
x_{da}\\
y_d\\
0\\
1
\end{pmatrix}=\begin{pmatrix}
\frac {x\cdot cot(\frac{\alpha}2)}{ar\cdot z}\\
\frac {y\cdot cot(\frac{\alpha}2)}z\\
0\\
1
\end{pmatrix} = \frac1z \begin{pmatrix}
\frac {x\cdot cot(\frac{\alpha}2)}{ar}\\
y\cdot cot(\frac{\alpha}2)\\
0\\
z
\end{pmatrix}\sim \begin{pmatrix}
\frac {x\cdot cot(\frac{\alpha}2)}{ar}\\
y\cdot cot(\frac{\alpha}2)\\
0\\
z
\end{pmatrix}
\]
上述坐标用矩阵可以描述为
\[\begin{pmatrix}
\frac1{ar} &0 & 0 & 0\\
0 &1 & 0 & 0\\
0 &0 & 1 & 0\\
0 &0 & 0 & 1\\
\end{pmatrix}\begin{pmatrix}
cot(\frac{\alpha}2) & 0 & 0 & 0\\
0 & cot(\frac{\alpha}2) & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 1 & 0\\
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1\\
\end{pmatrix} \tag{A-1}
\]
在这里，没有使用\(z\)值，造成了中间矩阵为奇异阵。由于\(z=0\)，上述映射关系不是线性变换，更不是线性同构。
裁剪坐标系
为了使投影成为一种变换，需要将\(z\)值考虑进来，我们考虑线段的缩放： \([n,f] \to[-1,1]\) ，设\(f(z) = Az + B\)，经过透视除法之后结果变为下面的式子
\[A + \frac Bz
\]
将\(n,f\)代入上式，得
\[A + \frac Bn = -1 \\
A + \frac Bf = 1 \\
\]
\[\left.\begin{matrix}
A + \frac Bn = -1 \\
A + \frac Bf = 1
\end{matrix}\right\}\Rightarrow B(\frac1f-\frac1n) = 2 \Rightarrow B = \frac{2nf}{n-f}
\]
\[\left.\begin{matrix}
B = \frac{2nf}{n-f} \\
A + \frac Bf = 1
\end{matrix}\right\}\Rightarrow A = 1 - \frac{2n}{n-f} = \frac{-n-f}{n-f}
\]
我们将\((A-1)\)式中第三行替换成\([0 ,0, A, B]\), \((A-1)\)式变成
\[\begin{pmatrix}
\frac1{ar} &0 & 0 & 0\\
0 &1 & 0 & 0\\
0 &0 & 1 & 0\\
0 &0 & 0 & 1\\
\end{pmatrix}\begin{pmatrix}
cot(\frac{\alpha}2) & 0 & 0 & 0\\
0 & cot(\frac{\alpha}2) & 0 & 0\\
0 & 0 & \frac{-n-f}{n-f} & \frac{2nf}{n-f}
\\
0 & 0 & 1 & 0\\
\end{pmatrix}\begin{pmatrix}
x\\
y\\
z\\
1\\
\end{pmatrix} =\begin{pmatrix}
\frac {x\cdot cot(\frac{\alpha}2)}{ar}\\
y\cdot cot(\frac{\alpha}2)\\
Az+B\\
z
\end{pmatrix}\sim \begin{pmatrix}
\frac {x\cdot cot(\frac{\alpha}2)}{z\cdot ar}\\
\frac{y\cdot cot(\frac{\alpha}2)}z\\
A+\frac Bz\\
1
\end{pmatrix} \tag{A-2}
\]
最终的变换矩阵如下：
\[\begin{pmatrix}
\frac1{ar}cot(\frac{\alpha}2) & 0 & 0 & 0\\
0 & cot(\frac{\alpha}2) & 0 & 0\\
0 & 0 & \frac{-n-f}{n-f} & \frac{2nf}{n-f}
\\
0 & 0 & 1 & 0\\
\end{pmatrix}\tag{A-3}
\]
在用投影矩阵乘上顶点坐标之后，顶点坐标被变换到我们所说的裁剪坐标系之下，在执行透视除法之后顶点坐标被变换到了 NDC 坐标系（NormalizedDeviceCoordinates）之下。
在\(\alpha\neq 0,n\neq f\)的情况下，\((A-3)\)式矩阵可逆矩阵，其变换为线性变换，并且是同构变换。
