scheme集合的表示

集合，就是一些不同形象的汇集，或者说，通过一组可以作用于“集合”的操作来定义他们。
集合的一种表示方式是用其元素的表，其中任何一种元素都不超过一次。对于这种表达形式，可以通过一种操作保证集合元素不是符号。
(define (element-of-set? x set)
(cond ((null? set) #f)
((equal? x (car set)) #t)
(else (element-of-set? x (cdr set)))))
利用它可以写出adjoin-set。
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
求交集：
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
求并集：
(define (union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
((element-of-set? (car set1) set2)
(union-set (cdr set1) set2))
(else (cons (car set1) (union-set (cdr set1 set2))))))
练习2.60 如果采用有重复元素的表来表示集合，对操作有什么影响？
有重复内容，上述操作改写为:

点击查看代码

(define (element-of-set? x set)
    (cond ((null? set) #f)
          ((equal? x (car set)) #t)
          (else (element-of-set? x (cdr set)))))
(define (adjoin-set x set)
    (append set x))
(define (intersection-set set1 set2)
    (cond ((or (null? set1) (null? set2)) '())
          ((element-of-set? (car set1) set2)
           (cons (car set1)
                 (intersection-set (cdr set1) set2)))
          (else (intersection-set (cdr set1) set2))))
(define (union-set set1 set2)
    (append set1 set2))

重复情况下需要消耗更多内存空间，并且查找起来更慢。

作为排序的表的情况下，部分操作可以减少较多时间和空间占用。
练习2.61 如果表是有排序的情况下，如何实现adjoin？

点击查看代码

(define (adjoin-set x set)
    (cond ((null? set) (list x))
          ((= x (car set)) set)
          ((< x (car set)) (cons x set))
          (else (cons (car set) (adjoin-set x (cdr set))))))

练习2.62 在排序情况下实现union-set的操作

点击查看代码

(define (union-set set1 set2)
    (cond ((null? set1) set2)
          ((null? set2) set1)
          (else (let ((x1 (car set1)) (x2 (car set2)))
                    ((= x1 x2) (cons x1 (union-set (cdr set1) (cdr set2))))
                    ((< x1 x2) (cons x1 (union-set (cdr set1) set2)))
                    ((< x2 x1) (cons x2 (union-set set1 (cdr set2))))))))

将集合作为二叉树进行表示，同样可以实现上述操作，通过实例Huffman编码树体现。 练习2.67 完成一棵编码树和一个样例消息的编码

点击查看代码

(define sample-tree
    (make-code-tree (make-leaf 'A 4)
                    (make-code-tree
                     (make-leaf 'B 2)
                     (make-code-tree (make-leaf 'D 1)
                                     (make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))

(decode sample-message sample-tree) 
(A D A B B C A)

练习2.68 过程encode以一个消息和一棵树为参数，产生被编码消息的二进制表：

点击查看代码

(define (encode message tree)
    (if (null? message)
        '()
        (append (encode-symbol (car message) tree)
                (encode (cdr message) tree))))
(define (encode-symbol symbol tree)
    (if (leaf? tree)
        (if (eq? symbol (symbol-leaf tree)) 
            '() 
            #f)
        (let ((left-result (encode-symbol symbol (left-branch tree))))
             (if left-result
                (cons 0 left-result)
                (let ((right-result (encode-symbol symbol (right-branch tree))))
                    (if right-result
                        (cons 1 right-result)
                        #f))))))

练习2.69 编写一个过程通过归并集合中最小权重的元素生成Huffman编码树。

点击查看代码

(define (generate-huffman-tree pairs)
    (sucessive-merge (make-leaf-set pairs)))
(define (sucessive-merge pairs)
    (if (= (length pairs) 1)
        (car pairs)
        (let ((left (car pairs))
              (right (cadr pairs))
              (remained (cddr pairs)))
              (sucessive-merge (adjoin-set (make-code-tree left right) remained)))))

练习2.70 编码给定消息
(define tree (generate-huffman-tree '((A 2)
(NA 16)
(BOOM 1)
(SHA 3)
(GET 2)
(YIP 9)
(JOB 2)
(WAH 1))))
(define messages '((GET A JOB)
(SHA NA NA NA NA NA NA NA NA)
(GET A JOB)
(SHA NA NA NA NA NA NA NA NA)
(WAH YIP YIP YIP YIP YIP YIP YIP YIP YIP)
(SHA BOOM)))

点击查看代码

(define (encode-message message tree)
    (if (null? message)
        '()
        (append (encode (car message) tree)
         (encode-message (cdr message) tree))))

(encode-message messages tree)
(1 1 1 1 1 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1
1 1 1 0 0 1 1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 0 1
0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1)
该编码共84位二进制，如果采用三位的定长编码，共36个字符，供需108位二进制，采用变长编码节省了24位。

练习2.71 如果有一颗n个符号的字母表Huffman字母表，且相对频率为1、2、4、……、2^(n-1)，请勾勒n=5和n=10的有关树的样子。

点击查看代码

(generate-huffman-tree '((A 1) (B 2) (C 4) (D 8) (E 16)))
(((((leaf A 1) (leaf B 2) (A B) 3) (leaf C 4) (A B C) 7)
   (leaf D 8)
   (A B C D)
   15)
  (leaf E 16)
  (A B C D E)
  31)

n=5时：

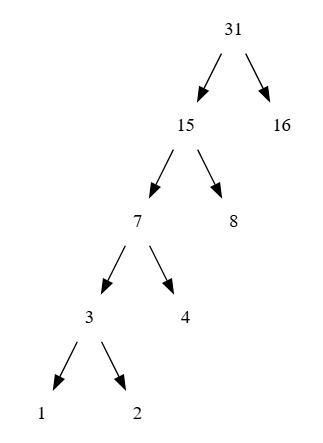
出现最频繁的符号在右上角，即1位二进制位，最不频繁的符号在左下角，需要n-1位二进制。

练习2.72 针对2.71的编码，步数的增长速率是甚么？
最频繁的符号步数增长，因为最频繁的符号都在右上角，需要对左树的进行遍历后才能到达右上，n=1，步数为1；n=2，步数为3；n=3，步数为5。以此类推，遍历步数为2n-1。
最不频繁的符号的步数，只需要遍历左树，步数为n。