create_frustum 分析（frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)）

    def create_frustum(self):
        """Generate frustum"""
        # make grid in image plane
        ogfH, ogfW = self.final_dim  #256, 704
        fH, fW = ogfH // self.downsample_factor, ogfW // self.downsample_factor  #[16, 44]
        d_coords = torch.arange(*self.d_bound,   #self.d_bound      [2.0, 58.0, 0.5]
                                dtype=torch.float).view(-1, 1,
                                                        1).expand(-1, fH, fW)
        D, _, _ = d_coords.shape #[112, 16, 44]                 2,  2.5, 3, 3.5, 4, 4.5,..., 58
        x_coords = torch.linspace(0, ogfW - 1, fW, dtype=torch.float).view(
            1, 1, fW).expand(D, fH, fW)
        y_coords = torch.linspace(0, ogfH - 1, fH,
                                  dtype=torch.float).view(1, fH,
                                                          1).expand(D, fH, fW)
        paddings = torch.ones_like(d_coords)

        # D x H x W x 3
        frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)
        return frustum

d_coords = torch.arange(*[2, 5, 0.5], dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)

fH=5
fW=7
d_coords = torch.arange(*[2, 5, 0.5],
dtype=torch.float).view(-1, 1,
1).expand(-1, fH, fW)
输出
我们来逐步解析这段 PyTorch 代码，看看最终变量 d_coords 的输出形状和内容。

代码解析：

fH = 5
fW = 7
d_coords = torch.arange(*[2, 5, 0.5], dtype=torch.float)  # 等价于 torch.arange(2, 5, 0.5)

`torch.arange(2, 5, 0.5)`

会生成从 2 到小于 5 的数，步长为 0.5：

tensor([2.0, 2.5, 3.0, 3.5, 4.0, 4.5])

这是一个 shape 为 [6] 的张量。

然后：

.view(-1, 1, 1)

把 shape 从 [6] 变成 [6, 1, 1]

接着：

.expand(-1, fH, fW)

扩展为 [6, 5, 7]

最终结果

d_coords 是一个 shape = [6, 5, 7] 的张量，其中：

第一维是 6，对应的是 d 维的变化（从 2 到 4.5，步长 0.5）
每一个 [i, :, :] 切片都是一个 5x7 的矩阵，数值全部是同一个值（对应每个 d 的值）

简要输出（示例）：

d_coords[0]  # 对应值为 2.0 的切片
# tensor([
#     [2., 2., 2., 2., 2., 2., 2.],
#     [2., 2., 2., 2., 2., 2., 2.],
#     [2., 2., 2., 2., 2., 2., 2.],
#     [2., 2., 2., 2., 2., 2., 2.],
#     [2., 2., 2., 2., 2., 2., 2.]
# ])

类似地，d_coords[1] 是全是 2.5，d_coords[2] 是全是 3.0，…… 直到 d_coords[5] 是全是 4.5。

需要我帮你可视化一下输出或打印全部内容吗？
好的，我们来打印 d_coords 的全部内容。

原始代码回顾：

import torch

fH = 5
fW = 7
d_coords = torch.arange(2, 5, 0.5, dtype=torch.float).view(-1, 1, 1).expand(-1, fH, fW)

打印结果（完整输出）：

tensor([[[2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000],
         [2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000],
         [2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000],
         [2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000],
         [2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000, 2.0000]],

        [[2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000],
         [2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000],
         [2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000],
         [2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000],
         [2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000, 2.5000]],

        [[3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000],
         [3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000],
         [3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000],
         [3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000],
         [3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000, 3.0000]],

        [[3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000],
         [3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000],
         [3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000],
         [3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000],
         [3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000, 3.5000]],

        [[4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000],
         [4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000],
         [4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000],
         [4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000],
         [4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000, 4.0000]],

        [[4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000],
         [4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000],
         [4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000],
         [4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000],
         [4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000, 4.5000]]])

每一层是一个 5x7 的矩阵，对应一个深度层的标量值填充。
需要我帮你把这个东西拼成 3D 可视化形式或者可用在卷积操作中的坐标 grid 吗？

x_coords = torch.linspace(0, 100 - 1, fW, dtype=torch.float).view( 1, 1, fW).expand(6, fH, fW)

我们来分析这段代码：

原始代码

x_coords = torch.linspace(0, 100 - 1, fW, dtype=torch.float).view(1, 1, fW).expand(6, fH, fW)

前提

fW = 7
fH = 5
所以 (6, fH, fW) 表示输出 shape 是 [6, 5, 7]，与 d_coords 一样

分解解析：

1. `torch.linspace(0, 100 - 1, fW, dtype=torch.float)`

等价于：

torch.linspace(0, 99, 7)

它在 0 到 99 之间均匀采样 7 个数：

tensor([ 0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000])

这是一个形状为 [7] 的张量。

2. `.view(1, 1, fW)`

变成 [1, 1, 7] 的张量。

3. `.expand(6, fH, fW)`

变成 [6, 5, 7]，也就是：

扩展出 6 个深度通道（第一维）
每个是一个 5x7 的矩阵
每一行都是相同的： [0, 16.5, 33, 49.5, 66, 82.5, 99]

最终结果 `x_coords` 结构：

x_coords[0]
# tensor([
#     [0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000],
#     [0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000],
#     [0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000],
#     [0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000],
#     [0.0000, 16.5000, 33.0000, 49.5000, 66.0000, 82.5000, 99.0000]
# ])

每个深度层都是相同的 5x7 网格，其中每一行都是线性从 0 到 99 的值（7 列）。

如果你之前的 d_coords 表示的是 depth，x_coords 就是横向位置（列坐标）。你是不是在构建一个 3D voxel grid 的坐标 map？可以继续配上 y_coords 就齐了。需要我给你生成 y_coords 一起组成完整坐标吗？

y_coords = torch.linspace(0, 50 - 1, fH, dtype=torch.float).view(1, fH,1).expand(6, fH, fW)

完美！你这段代码和前面的 d_coords、x_coords 一起配合，刚好构建了一个 3D 网格坐标系（depth, height, width）。我们再来逐步解析你这最后一块 y_coords 的代码：

代码

y_coords = torch.linspace(0, 50 - 1, fH, dtype=torch.float).view(1, fH, 1).expand(6, fH, fW)

参数回顾：

fH = 5
fW = 7

分解过程：

1. `torch.linspace(0, 50 - 1, fH)`

等价于 torch.linspace(0, 49, 5)：

输出为 5 个在 0 ~ 49 均匀分布的数：

tensor([ 0.0000, 12.2500, 24.5000, 36.7500, 49.0000])

形状 [5]

2. `.view(1, fH, 1)` → `[1, 5, 1]`

3. `.expand(6, fH, fW)` → `[6, 5, 7]`

每一行是一样的值（即同一高度）
每个 5x7 区域中，行与行之间不同，列是复制的

最终输出结构（示意）：

y_coords[0]
# tensor([
#     [ 0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000,  0.0000],
#     [12.2500, 12.2500, 12.2500, 12.2500, 12.2500, 12.2500, 12.2500],
#     [24.5000, 24.5000, 24.5000, 24.5000, 24.5000, 24.5000, 24.5000],
#     [36.7500, 36.7500, 36.7500, 36.7500, 36.7500, 36.7500, 36.7500],
#     [49.0000, 49.0000, 49.0000, 49.0000, 49.0000, 49.0000, 49.0000]
# ])

每个切片 [i,:,:] 都是一样的坐标结构。

总结

现在你有了：

d_coords: 每个 voxel 的 depth 坐标（共6层）
y_coords: 每个 voxel 的 height 坐标（5行）
x_coords: 每个 voxel 的 width 坐标（7列）

如果你要拼成一个完整的 (D, H, W, 3) 的网格坐标点，可以这样做：

coords = torch.stack((x_coords, y_coords, d_coords), dim=-1)
# shape: [6, 5, 7, 3]

这样每个 voxel 的 [x, y, d] 坐标就齐活了！

要不要我给你画一下这三维坐标的切片图示？或者打包成 point cloud？

frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)

        paddings = torch.ones_like(d_coords)

        # D x H x W x 3
        frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)

漂亮！你这波操作看起来是要构建一个 frustum grid ——也就是相机视锥体中的稀疏体素坐标，用于后续投影到 3D 世界坐标系或做体积渲染的。我们来逐步看你最后的这两行干了啥：

代码解析

paddings = torch.ones_like(d_coords)

结果：

paddings 是一个全是 1 的张量，形状为 [6, 5, 7]（即 D × H × W）
用于后续与投影矩阵相乘时的 齐次坐标补一（homogeneous coordinate）

然后：

frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)

d_coords.shape = torch.Size([6, 5, 7]) # D x H x W
x_coords.shape = torch.Size([6, 5, 7]) # 每个 voxel 的 x 坐标
y_coords.shape = torch.Size([6, 5, 7]) # 每个 voxel 的 y 坐标
paddings.shape = torch.Size([6, 5, 7]) # 全是 1 的齐次项

frustum.shape = torch.Size([6, 5, 7, 4]) # 每个 voxel 是一个 4D 齐次坐标 [x, y, d, 1]

含义：

把每个 voxel 的 [x, y, d, 1] 坐标合并成一个向量
最后一维 -1 是沿着最后一维拼接
得到的 frustum 形状为 [6, 5, 7, 4]

也就是：

每个 voxel 有一个 [x, y, d, 1] 齐次坐标

示例：

frustum[0, 0, 0] 的内容：

tensor([0.0000, 0.0000, 2.0000, 1.0000])

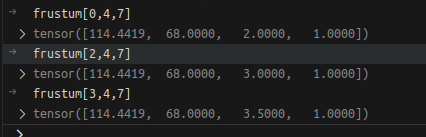
frustum[0, 4, 6]：

tensor([99.0000, 49.0000, 2.0000, 1.0000])

用途

这就是你要把体素网格从 frustum 坐标（图像视角）映射到相机或世界坐标系前的准备工作。通常下一步是：

# projection or transformation
points_3D = frustum @ intrinsics_inv.T @ extrinsics_inv.T

或者用于 BEV（Bird’s Eye View）场景感知网络里从图像到 3D 的几何变换。

总结一下结构：

d_coords: depth，沿 z 方向
y_coords: height，沿 y 方向
x_coords: width，沿 x 方向
paddings: 齐次项，全是 1
frustum: [D, H, W, 4]，每个 voxel 的 [x, y, d, 1]

如果你接下来要做投影到世界坐标、点云投影、深度渲染等，随时说，我可以帮你接着撸下去🔥
你现在在做 BEVFusion 类似的 3D 感知网络吗？还是别的项目？

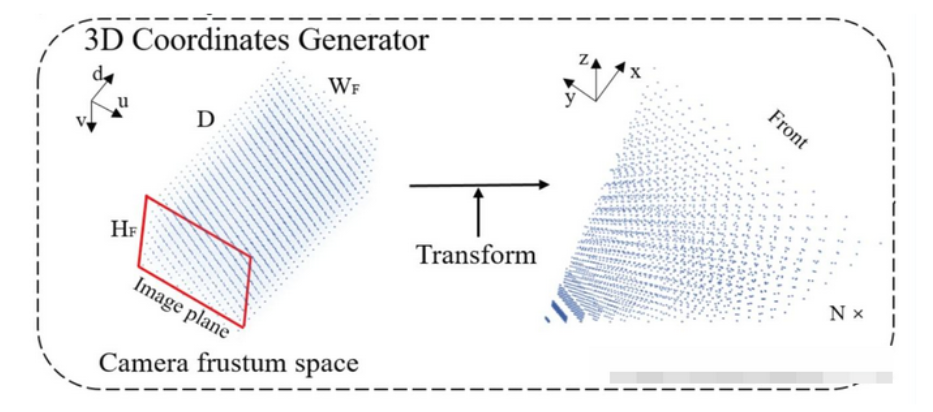
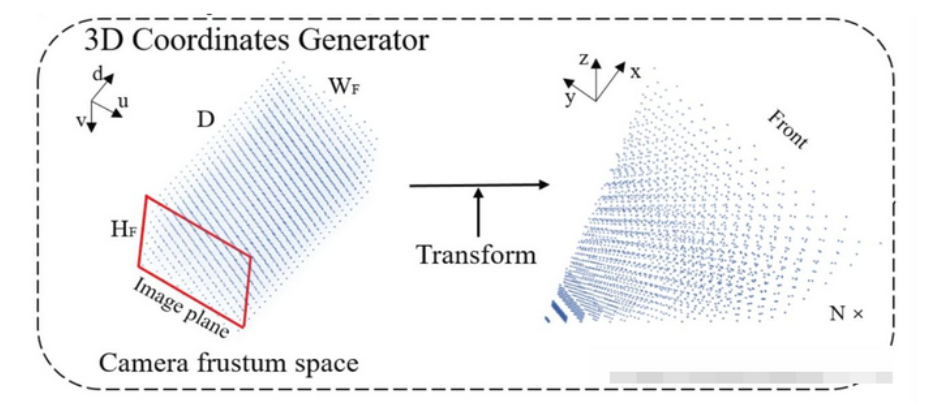
上面的操作就是得到如下图左边部分，

其他例子：

posted @ 2025-04-17 11:39 无左无右阅读(23) 评论(0) 收藏举报

刷新页面返回顶部

无左无右

create_frustum 分析 （frustum = torch.stack((x_coords, y_coords, d_coords, paddings), -1)）