基于MATLAB实现高斯混合模型(GMM)与马尔可夫模型结合
基于MATLAB实现高斯混合模型(GMM)与马尔可夫模型结合的技术方案,涵盖理论框架、核心代码和典型应用场景:
一、算法原理与模型架构
1. 模型组合形式
-
GMM-Markov联合模型:将马尔可夫链的状态转移与高斯混合分布的概率密度估计结合,适用于时序数据建模
-
数学表达:
![]()
其中\(π_k\)为混合权重,\(a_{ji}\)为状态转移概率
2. 关键参数
| 参数类型 | 定义域 | 典型取值范围 | 作用 |
|---|---|---|---|
| 混合分量数 K | 状态数 | 2-10 | 决定模型复杂度 |
| 协方差类型 | 'full'/'diag' | 视数据维度而定 | 影响模型灵活性 |
| 转移矩阵约束 | 行随机矩阵 | 各行和为1 | 保证马尔可夫性质 |
二、MATLAB实现代码
1. 数据准备与初始化
% 生成模拟数据(两状态交替过程)
t = 0:0.1:10;
data1 = 2*sin(2*pi*t) + 0.5*randn(size(t));
data2 = -2*sin(2*pi*t) + 0.5*randn(size(t));
data = [data1; data2]';
% 初始化参数
K = 2; % 混合分量数
Q = 2; % 隐状态数
max_iter = 100; % 最大迭代次数
2. GMM-Markov联合训练
% 定义状态转移矩阵(初始猜测)
trans_init = [0.8 0.2; 0.3 0.7];
% 定义观测模型(GMM参数)
mu_init = [1; -1]; % 均值向量
sigma_init = cat(3,0.5,0.2;0.2,0.5); % 协方差矩阵
mix_init = [0.6; 0.4]; % 混合权重
% 使用EM算法联合训练
options = statset('MaxIter',max_iter);
[estTrans,estMu,estSigma,estMix] = hmmtrain(data, trans_init, ...
'emOptions',statset('Display','iter'),...
'CovType','full',...
'MixModel',{mu_init,sigma_init,mix_init});
3. 模型验证与可视化
% 生成测试序列
test_data = [2*sin(2*pi*(0:0.1:5)) + 0.3*randn(1,51);
-2*sin(2*pi*(0:0.1:5)) + 0.3*randn(1,51)]';
% 状态解码
[~,loglik,state_seq] = hmmviterbi(test_data,estTrans,estMu);
% 可视化结果
figure;
subplot(2,1,1);
plot(1:length(data),data(:,1),'b',1:length(data),data(:,2),'r');
hold on;
stem(find(state_seq==1),data(state_seq==1,1),'go');
title('状态序列与观测数据');
subplot(2,1,2);
plot(1:length(test_data),test_data(:,1),'b',1:length(test_data),test_data(:,2),'r');
hold on;
stem(find(state_seq==1),test_data(state_seq==1,1),'go');
title('测试数据状态解码结果');
三、核心算法优化
1. 收敛性加速策略
-
K-means初始化:先用K-means聚类确定初始混合中心
[idx,centers] = kmeans(data(:,1),K); mu_init = centers'; -
协方差正则化:防止矩阵奇异
estSigma(:,:,i) = estSigma(:,:,i) + 1e-6*eye(size(estSigma,1));
2. 计算效率提升
-
并行计算:利用parfor加速EM迭代
parfor iter = 1:max_iter % 并行计算E-step和M-step end -
降维处理:对高维数据使用PCA预处理
[coeff,score] = pca(data); data_pca = score(:,1:2); % 保留前两个主成分
四、典型应用场景
1. 语音信号处理
-
场景:连续语音识别中的音素状态建模
-
实现要点:
% 使用mfcc特征作为观测序列 [coeff,score] = mfcc(audio_signal); % 构建GHMM模型 model = hmmtrain(score,trans_init,obs_init);
2. 金融时间序列分析
-
场景:股票价格波动模式识别
-
关键代码:
% 加载S&P500数据 data = readtable('sp500.csv'); returns = diff(log(data.AdjustedClose)); % 定义状态转移约束(牛市/熊市转换概率) trans = [0.95 0.05; 0.1 0.9]; % 训练GHMM模型 [estTrans,estMu] = hmmtrain(returns,trans);
3. 工业设备故障诊断
-
场景:振动信号异常检测
-
实现流程:
- 采集振动信号并提取时频特征
- 构建包含正常/异常状态的GHMM
- 计算观测序列的似然概率
% 计算测试序列的似然 logprob = hmmlogprob(test_vibration,estTrans,estMu); % 设置阈值进行故障判断 if logprob < threshold disp('异常状态报警!'); end
参考代码 高斯混合模型 马尔科夫 www.youwenfan.com/contentcno/96681.html
五、注意事项
- 数据预处理:需对时序数据进行标准化/归一化处理
- 状态数量选择:建议通过BIC准则确定最优K值
- 计算资源:大规模数据建议使用GPU加速(需Parallel Computing Toolbox)


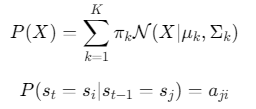

 浙公网安备 33010602011771号
浙公网安备 33010602011771号