一元二次方程，二次函数及一元二次不等式学习笔记

前言：

三个二次之间有着微妙的联系，于是在放一块写了

一元二次方程

一元二次方程的定义

定义：一元二次方程是只含有一个未知数，且未知数的最高次数是二次的多项式方程。

——摘自某百科

显然的，对于任意一元二次方程，化简之后都可以表示为 $ ax^2 + bx + c = 0 ( a \ne 0 ) $ 的形式。

一元二次方程的形式

一般形式：$ ax^2 + bx + c = 0 ( a \ne 0 ) $

两根式：$a ( x - x_1 )( x - x_2 ) = 0 ( a \ne 0 ) $，其中 $ x_1, x_2 $ 为方程两根（注意：当且仅当二次方程有解时该方程存在两根式）。

过多形式这里不在赘述。（形式啥的本来就不重要）

一元二次方程的根

解一元二次方程

解一元二次方程一般有 开平方法，配方法，因式分解法，求根公式法等。

开平方法：

适用于形如 $ ( px + q )^2 = m (p \ne 0, m \ge 0) $ 的方程。

直接对方程两边开根，得到 $ px + q = \pm \sqrt m $，然后解两个一元一次方程即可

配方法：

适用于一般形式的一元二次方程。

所谓 “配方”，就是把一般方程转化为平方的形式，然后使用开平方法。

以方程 $ x^2 + 2x - 3 = 0 $ 为例：

配方：

\[x^2 + 2x + 1 - 4 = 0 \]

\[( x + 1 )^2 = 4 \]

套用开平方法得到：

\[x + 1 = \pm 2 \]

故原方程的两根分别为 $ x_1 = 1, x_2 = -3 $

如果二次项系数不为 1，则可令方程两边同时除以二次项系数，转化为二次项系数为 1 的形式。

因式分解法：

观察两根式：

\[a( x - x_1 )( x - x_2 ) = 0 \]

将其展开：

\[a(x^2 - (x_1 + x_2)x + x_1 x_2) = 0 \]

\[ax^2 - a (x_1 + x_2)x + a x_1 x_2 = 0 \]

反过来就是因式分解法解方程的步骤。

因式分解法就是利用瞪眼法瞪出来方程的两根。

再以方程 $ x^2 + 2x - 3 = 0 $ 为例：

\[ax^2 - a (x_1 + x_2)x + a x_1 x_2 = 0 \]

这里 $ a = 1 $，所以最终方程一定是 $ x^2 - (x_1 + x_2)x + x_1 x_2 = 0 $ 的形式,

所以要找到两个 $ x_1, x_2 $，使得 $ - (x_1 + x_2) = 2, x_1 x_2 = -3 $.

不难看出， 方程两根： $ x_1 = 1, x_2 = -3 $，

所以原方程可化为：$$ ( x - 1 )( x + 3 ) = 0 $$

故原方程的两根分别为 $ x_1 = 1, x_2 = -3 $

十字相乘法 是猜方程两根的一种直观的方法，中学生的必备技能了属于是。

求根公式法：

就在下面 \(\Downarrow\)

一元二次方程的求根公式

在 开平方法，配方法，因式分解法 中，显然最为一般的是配方法，求根公式的推导可以利用配方法：

对于一元二次方程 $ ax^2 + bx + c = 0 ( a\ne 0 ) $:

不妨设原方程有根，

把 $ a $，除过去：

\[x^2 + \frac{b}{a} + \frac{c}{a} = 0 \]

然后配方：

\[x^2 + \frac{b}{a} + (\frac{b}{2a})^2 - (\frac{b}{2a})^2 + \frac{c}{a} = 0 \]

\[( x + \frac{b}{2a} )^2 = \frac{b^2}{4a^2} - \frac{c}{a} \]

\[( x + \frac{b}{2a} )^2 = \frac{b^2 - 4ac}{4a^2} \]

两边同时开平方：

\[x + \frac{b}{2a} = \pm \sqrt \frac{b^2 - 4ac}{4a^2} \]

\[x = \frac{\pm \sqrt{b^2 - 4ac}}{2a} - \frac{b}{2a} \]

最终得到：

\[x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

一元二次方程是否存在实数根

由求根公式的推导过程可以得出，若方程有两实数根，则一定有 $ \sqrt{b^2 - 4ac} \ge 0 $（必要性）；反过来，若 $ \sqrt{b^2 - 4ac} \ge 0 $，则将 $ a,b,c $ 分别代入后，一定得出有对应的解，也就是方程定有；两实数根（充分性）。

所以，一元二次方程存在实数根的充要条件为 $ \sqrt{b^2 - 4ac} \ge 0 $

规定 $ \Delta = \sqrt{b^2 - 4ac} $ 为一个二次方程的判别式；

当 $ \Delta > 0 $ 时，原二次方程有两不等实根；

当 $ \Delta = 0 $ 时，原二次方程有两相等实根；

当 $ \Delta = 0 $ 时，原二次方程无实根。

注意：$ \Delta = 0 $ 时，并非“只有一实根”，而是“有两相等实根”。

一元二次方程根与系数的关系（韦达定理）

很 nb 一玩意

仍然假设二次方程中 $ \Delta \ge 0 $;

不妨设 $ x_1 \ge x_2 $

因为

\[x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

所以

\[x_1 + x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a} + \frac{-b - \sqrt{b^2 - 4ac}}{2a} \]

惊奇的发现根号可以消掉

\[x_1 + x_2 = -\frac{b}{a} \]

同样代入可以得出：

\[x_1 x_2 = \frac{c}{a} \]

可以看出，韦达定理的形式极其简便，可以大大减少计算量。

韦达定理常见变形：

$ a,b $ 为方程两根

$ a^2 + b^2, a^3 + b^3, \frac{1}{a} + \frac{1}{b}, \frac{a}{b} + \frac{b}{a}...$

其实随便化化柿子就出来了。

事实上，所有的关于 $ x_1,x_2 $ 的对称式都可以用两根和以及两根积的组合来表示。

注意：韦达定理的适用前提是原方程存在实根。

来几道题目：

1.已知方程 $ x^2 + x - 1 = 0 $ 的两根分别为 $ \alpha,\beta $，求 $ \alpha^2 + \alpha \beta + \beta^2 $ 的值。

分析：直接暴力求解肯定不现实，考虑对求解代数式整理后使用韦达定理。

由韦达定理得：

\[\alpha + \beta = -1,\alpha \beta = -1 \]

故

\[\alpha^2 + \alpha \beta + \beta^2 = ( \alpha + \beta)^2 - \alpha \beta = ( -1 )^2 - ( -1 ) = 2 \]

2.已知方程 $ x^2 + x - 1 = 0 $ 的两根分别为 $ \alpha,\beta $，求 $ 2\alpha^2 + \beta^2 + \alpha - 1 $ 的值。

分析：柿子变得有点复杂，不如考虑 $ \alpha $ 本身的意义。

将 $ \alpha $ 代入原式，有

\[\alpha^2 + \alpha - 1 = 0 \]

故

\[2\alpha^2 + \beta^2 + \alpha - 1 = \alpha^2 + \alpha - 1 + \alpha^2 + \beta^2 = ( \alpha + \beta )^2 - 2\alpha \beta = 3 \]

可见，韦达定理是非常之灵活的方法。

（非对称韦达）3.已知关于 $ x $ 的二次方程 $ (4k^2 + 1)x^2 + 8k^2x + 4k^2 - 4 = 0 $ 的两根分别为 $ x_1, x_2 $，求 $ \frac{x_1 x_2 + x_1 - 2x_2-2}{x_1 x_2 + 2x_1 + x_2 + 2} $ 的值.

分析：形式挺复杂，考虑使用韦达定理进行化简。

由韦达定理得：

\[x_1 + x_2 = -\frac{8k^2}{4k^2+1},x_1 x_2 = \frac{4k^2-4}{4k^2+1} \]

为方便表示，设 $ m = x_1 + x_2,n = x_1 x_2 $，接下来考虑 $ m,n $ 之间的关系，从而将求值式的 $ x_1 x_2 $ 换掉。

不难得出：

\[5m + 2n = -8 \]

得出这个代数式的方法有很多，但无一例外都很巧妙，这里给出一种：

最终我们要整理成 $ um + vn = w $ 的形式，而 $ m,n $ 两分式的分母代数式相同，考虑将分子配凑成其的倍数。

故

\[u \times (-8k^2) + v \times (4k^2-4) = w \times (4k^2+1) \]

即

\[(-8u + 4v)k^2 - 4v = 4wk^2 + w \]

所以就是求这个方程的一个解 \(\left\{\begin{matrix} -8u + 4v = 4w\\ -4v = w \end{matrix}\right.\)

把 $ w $ 消掉可以得出 $ u = \frac{5}{2} v $

再代入上上个柿子消掉 $ u $：

\[-16vk^2 - 4v = 4wk^2 + w \]

令 $ v = 1 $，得到 $ u = \frac{5}{2}, w = -4 $，

所以

\[\frac{5}{2}m + n = -4 \]

就是

\[5m + 2n = -8 \]

将 $ n $ 换掉：

\[n = \frac{-8-5m}{2} \]

\[\frac{x_1 x_2 + x_1 - 2x_2-2}{x_1 x_2 + 2x_1 + x_2 + 2} = \frac{n + x_1 - 2x_2-2}{n + 2x_1 + x_2 + 2} = \frac{\frac{-8-5m}{2} + x_1 - 2x_2-2}{\frac{-8-5m}{2} + 2x_1 + x_2 + 2} = \frac{-3x_1 - 9x_2 - 12}{-x_1 - 3x_2 - 4} = 3 \]

更简单的方法：

观察到一些特殊性质，考虑对后面那坨东西直接变形：

\[\frac{x_1 x_2 + x_1 - 2x_2-2}{x_1 x_2 + 2x_1 + x_2 + 2} = \frac{x_1 x_2 + x_1 + x_2 - 3x_2 - 2}{x_1 x_2 + 2(x_1 + x_2) - x_2 + 2} \]

\[= \frac{\frac{4k^2-4}{4k^2+1} -\frac{8k^2}{4k^2+1} - 3x_2 - 2}{\frac{4k^2-4}{4k^2+1} - 2 \times \frac{8k^2}{4k^2+1} - x_2+2} = \frac{4k^2-4-8k^2-3x_2(4k^2+1)-8k^2-2}{4k^2-4-16k^2-x_2(4k^2+1)+8k^2+2} \]

\[= \frac{-12k^2-3x_2(4k^2+1)-6}{-4k^2-x_2(4k^2+1)-2} = 3 \]

一些闲话：

大概这道题本来是直线 $ y = k(x+1) 与 $ 椭圆 $ C: \frac{x^2}{4} + y^2 = 1 $ 联立后求出来某个定值。但因为太抽象了就没法从结果推原题了。

在打下上一句话的 5min 后，xzy 推出来了，原题是这样：

已知椭圆 $ C:\frac{x^2}{4} + y^2 = 1 $，与 $ x $ 轴交点分别为 $ A(-2,0), B(2,0) $，过点 $ (-1,0) $ 作直线交椭圆 $ C $ 与点 $ M $, $ N \(。求证：\)$ \frac{k_{AM}}{k_{BN}} $ 为定值。

更一般地：对于椭圆 $ C:\frac{x^{2}} {a^{2}} + \frac{y^{2}} {b^{2}} $，过 $ x $ 轴某点 $ P(-x_0,0) $ 作直线交椭圆 $ C $ 与点 $ M,N $，则 $ \frac{k_{AM}} {k_{BN}} = \frac{a+x_0} {a-x_0} $（算了一节课算出来的），联立后方程为 $ (a^{2} k^{2} + b^{2} ) x^{2} + 2 a^{2} x_0 k^{2} x + a^{2} x_0 ^{2} k^{2} - a^{2} b^{2}=0 $，结果因式分解后为：

\[\frac{(a+x_{0})(a^{2} x_{0} k^{2} - a b^{2} + x_{2} (k^{2} a^{2} + b^{2}))} {(a-x_{0})(a^{2} x_{0} k^{2} - a b^{2} + x_{2} (k^{2} a^{2} + b^{2}))} \]

当 $ -x_0 = -c $ 时，$ \frac{k_{AM}}{k_{BN}} = \frac{a+c}{a-c} = \frac{1+e}{1-e} $。

二次函数

二次函数的定义

一般地，把形如 y = ax^2 + bx + c 的函数叫做二次函数，

其中 a 称为二次项系数，b 为一次项系数，c 为常数项。x 为自变量，y 为因变量。

等号右边自变量的最高次数是 2。

二次函数的形式

一般式：$ f(x) = ax^2 + bx + c ( a \ne 0 ) $

两根式：$ f(x) = a( x - x_1 )( x - x_2 ) $（注意：当且仅当二次函数有解时该函数存在两根式）

顶点式：$ f(x) = a( x - h )^2 + k $

二次函数的图像

可以发现二次函数的图像是抛物线.

其中二次函数尖尖的那个点叫做二次函数的顶点，顶点所在的关于 y 轴平行的直线叫做二次函数的对称轴。

图像不太重要，讲起来也比较麻烦。

不懂的话可以看看 这篇文章

二次函数的性质（代数）

函数零点与方程的根

以函数 $ f(x) = x^2 + 2x - 3 $ 为例：

令 $ f(x) = 0 $，得到 $ x^2 + 2x - 3 = 0 $，解得 $ x_1 = 1, x_2 = -3 $.

此时称，$ x_1, x_2 $ 为 $ f(x) $ 的零点.

可以发现，求解函数零点的过程实际上是在解一个关于自变量 $ x $ 的方程。

于是乎，一元二次方程的某些性质可以在二次函数上体现。

二次函数的对称性

由图像得， 二次函数是一个轴对称图形，下面给出证明：

\[f(x) = ax^2 + bx + c = a(x^2 + \frac{b}{a}) + c \]

\[= a( x^2 + \frac{b}{a}x + (\frac{b}{2a})^2 ) - \frac{b^2}{4a} + c \]

\[= a( x - \frac{b}{2a} )^2 + \frac{4ac - b^2}{4a} \]

这个东西叫做一个二次函数的顶点式，

所以 $ f(x) = a( x - h )^2 + k $ 中， $ h = \frac{b}{2a}, k = \frac{4ac - b^2}{4a} $.

令 $ x_1 = h - x_0, x_2 = h + x_0 $,

分别代入发现，$ f( x_1 ) = f( x_2 ) $,

$ x_1 $ 为 $ \mathbb{R} $ 上一值，所以二次函数关于 直线 $ x = h $ 对称。

二次函数的极值

显然，二次函数的极值在顶点处取到，下面给出证明：

当 $ a > 0 $ 时：$ a( x - h )^2 \ge 0, f(x) = a( x - h )^2 + k \ge k $ 当且仅当 $ x = h $ 时等号成立；

当 $ a < 0 $ 时：$ a( x - h )^2 \le 0, f(x) = a( x - h )^2 + k \le k $ 当且仅当 $ x = h $ 时等号成立.

所以我们得到了顶点坐标公式： $ ( h, k ) $，即 $ (-\frac{b}{2a}, \frac{4ac-b^2}{4a} ) $

抛物线的性质（解析几何）

抛物线的相似性

乱搞出来的一个命题，没啥用，但挺有意思.

求证：所有的抛物线都相互相似.

证明：

对于任意抛物线，都有对于函数顶点式 $ y = a( x - h )^2 + k $，将其顶点挪到 $ ( 0, 0 ) $，不改变其形状。这一步操作后我们只需证明所有形如 $ y = ax^2 $ 的抛物线相似。

显然所有形如 $ y = ax^2 $ 的抛物线相似。

对于任意抛物线 $ f(x) = a_1 x^2 ,g(x) = a_2 x^2 (a_1,a_2 \ne 0)) $，记 $ k = \frac{a_1}{a_2} $，则 $ \forall x \in \mathbb{R} $，有 $ f(x) = k \cdot g(x) $，证毕.

抛物线的焦点与准线

我不会，长大后再学习.

一元二次不等式

其实就是一元二次方程的 plus 版.

以不等式 $ x^2 + 2x - 3 \le 0 $ 为例：

可以构造函数 $ f(x) = x^2 + 2x - 3 $，并令 $ f(x) \le 0 $，画出 $ f(x) $ 的图像。

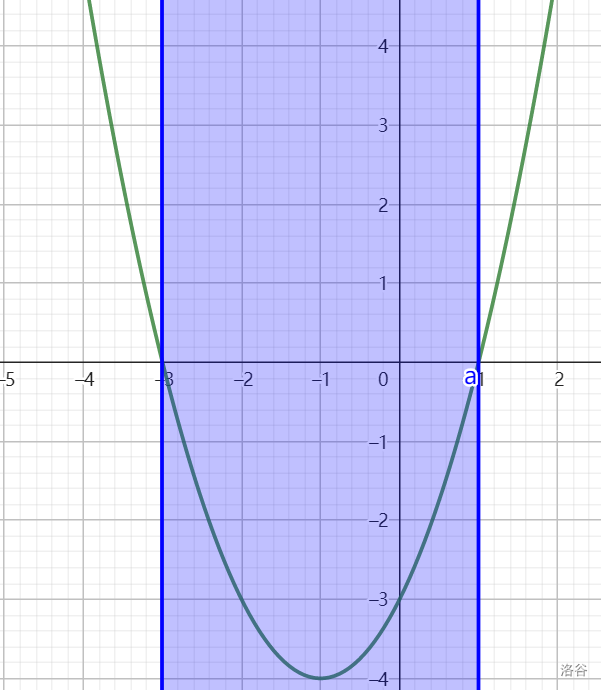
观察其在 $ x $ 轴下方区域在 $ x $ 轴的投影，进而得出解集.