反比例函数学习笔记

反比例函数的定义：

一般地，如果两个变量 x、y 之间的关系可以表示成 y = k/x (k 为常数，k ≠ 0)的形式，
那么称 y 是 x 的反比例函数.
--百度百科

反比例函数一般形式为 $ y = \frac{k}{x} $，其中 $ k \in \mathbb{R}$ 且 $ k \ne 0 $

也可以写作这两种形式：

$ y = kx^{-1} $，其中 $ k \in \mathbb{R}$ 且 $ k \ne 0 $

$ xy = k $，其中 $ k \in \mathbb{R}$ 且 $ k \ne 0 $

通常情况下都写一般形式，第二种较少，第三种可以用来做题推一些奇妙の结论.

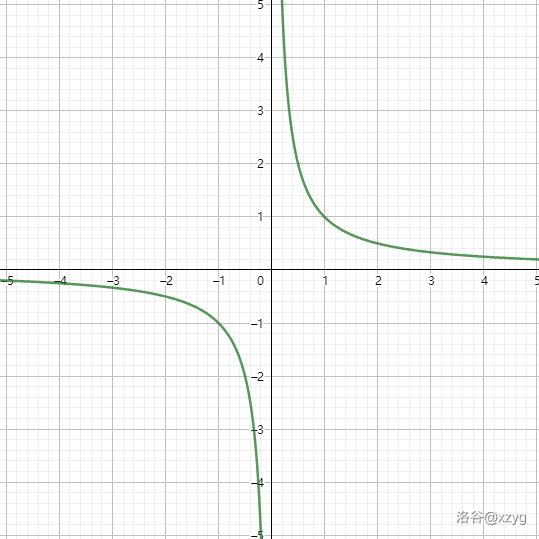
这个就是 $ y = \frac{1}{x} $ 的图像.读者可以将下面的性质与图像相结合食用.

反比例函数的性质：

1. 反比例函数图像不与坐标轴相交.

根据 $ xy = k $ 且 $ k \ne 0 $ 知，$ x $ 与 $ y $ 也必定是非零实数，即 $ x \ne 0,y \ne 0 $，而与两坐标轴重合的直线解析式分别为 $ x = 0,y = 0 $.

2. 反比例函数图像上任意一点 $ P $ 的横纵坐标之积为 k.

设点 $ P $ 坐标为 $ (m,n) $，则有 $ mn = k $.

可以发现，两边同时加绝对值也成立，即 $ |mn| = |k| $.过点 $ P $ 分别向两坐标轴作垂线，$ | mn | $ 正好是形成的矩形的面积.（P.S. 这个结论可以推出更多奇奇怪怪的结论，是九年级大多数反比例题目的 (祖宗) 根源.）

3. 当 $ k > 0 $ 时，反比例函数过一、三象限，当 $ k < 0 $ 时，反比例函数过二、四象限.

当 $ k > 0 $ 时，$ xy > 0 $, $ x,y $ 同号，即 $ x,y $ 在一、三象限.

当 $ k < 0 $ 时，$ xy < 0 $, $ x,y $ 异号，即 $ x,y $ 在二、四象限.

4. 当 $ k > 0 时 $，反比例函数分别在区间 $ (-\infty,0).(0,+\infty) $ 上单调递减；当 $ k < 0 时 $，反比例函数分别在区间 $ (-\infty,0).(0,+\infty) $ 上单调递增.

证明？读者自证罢(

更多的性质懒得列出来了...

这里再补充几条常用的结论（从易到难）：

1. 如下图，点 $ A $ 为 $ x $ 轴上一点，点 $ B $ 为 $ y $ 轴上一点，四边形 $ OACB $ 为矩形，则有：$ \frac{CD}{AD} = \frac{CE}{BE} $.

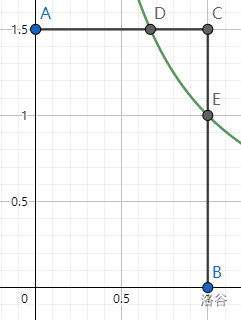
首先考虑使用相似三角形进行证明，然鹅题目并没有几个相等的角，并且考虑到反比例函数的性质，自然想到使用等积法证明。

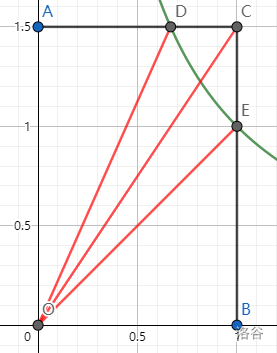
如图，连接 $ OD,OC,OE $.

不难得到:$ S_{\triangle AOD} = S_{\triangle BOE},S_{\triangle AOC} = S_{\triangle BOC} $

作一下差：$ S_{\triangle AOC} -S_{\triangle AOD} = S_{\triangle BOC} - S_{\triangle BOE} $

即：$ S_{\triangle OCD} = S_{\triangle OCE} $

因此 $ \frac{S_{\triangle OCD}}{S_{\triangle AOD}} = \frac{S_{\triangle OCE}}{S_{\triangle BOE}} $

故：$ \frac{CD}{AD} = \frac{CE}{BE} $.

2. 如下图，点 $ P $ 为反比例函数图像上一点，过点 $ P $ 作反比例函数的切线，分别交 $ x $ 轴，$ y $ 轴于点 \(A,B\)，则 $ AP = BP $.

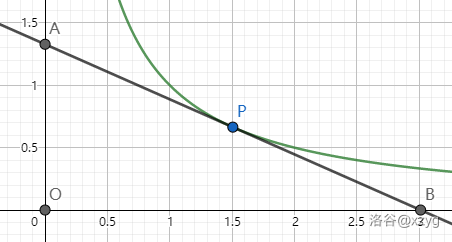
证法 1：

设直线 \(AB\) 解析式为 $ y_{AB} = mx + n $，令其与反比例函数相交，

化简后得到一个一元二次方程，其两根即为直线与反比例函数图像两交点的横坐标.

再令其 $ \Delta = 0 $，解出 $ m,n,k $ 之间的关系，暴力验证即可.

证法 2：

对 $ y = \frac{k}{x} $ 求导，可以得到：$ y' = -\frac{k}{x^2} $.

设 $ P(i,\frac{k}{i}) $，则直线 $ AB $ 可设为 $ y_{AB} = -\frac{k}{i^2}x + b $.

将 $ P(i,\frac{k}{i}) $ 代入，得：$ \frac{k}{i} = -\frac{k}{i^2} \cdot i + b \(，\) b = \frac{2k}{i} $.

所以，$ y_{AB} = -\frac{k}{i^2}x + \frac{2k}{i} $，

$ A(0,\frac{2k}{i}),B(2i,0) $，故 $ AP = BP $.