机器学习 —— 数理统计 —— 无偏估计的方差
无偏估计的方差
DeepSeek 思考:
嗯,用户问的是“无偏估计的方差”,这应该是在统计学中的内容。首先,我得回忆一下什么是无偏估计。无偏估计指的是估计量的期望等于被估计参数的真实值,也就是说,这个估计量在多次抽样下不会有系统性的偏差。那方差的无偏估计,可能指的是样本方差的无偏估计,通常用的是n-1作为分母的那个公式。
不过,用户可能想知道更详细的推导或者为什么用n-1而不是n。这时候需要解释为什么样本方差的分母是n-1才能得到无偏估计。可能涉及期望值的计算,证明E(s²) = σ²,其中s²是用n-1计算得到的样本方差。
另外,用户可能在实际应用中对这个概念有疑问,比如在数据分析中为什么软件默认使用n-1,或者是否所有情况下都用n-1。可能需要提到自由度的问题,以及当估计均值的时候,已经用了一个参数,所以自由度减少了一个,导致分母是n-1。
还有可能用户遇到了具体的问题,比如在计算方差时使用了不同的分母,导致结果有偏,所以想知道如何纠正。这时候需要给出具体的公式和例子,说明如何调整计算方式以获得无偏估计。
另外,可能需要注意用户是否混淆了方差的无偏估计和样本方差的计算。比如,总体方差σ²的无偏估计是样本方差s² = Σ(x_i - x̄)^2 / (n-1),而用n作为分母的话是有偏的,偏差随着样本量增大而减小。
还需要考虑用户的知识背景,是否了解期望、方差这些基本概念,是否需要从基础讲起。如果用户是学生,可能需要详细的数学推导;如果是实际应用者,可能需要更简洁的解释和实际例子。
也有可能用户的问题涉及到更复杂的估计量,比如在多变量分析中或者其他统计方法中的无偏方差估计,这时候需要进一步澄清问题的范围。但根据当前的问题,可能更偏向于基础的单变量样本方差的无偏估计。
总之,需要先确认用户的问题点,然后详细解释为什么n-1可以得到无偏估计,可能的数学证明,以及实际应用中的注意事项。同时,可能需要提醒用户注意区分总体方差和样本方差,以及在何种情况下使用哪种计算方式。



其实,这个n-1要想搞明白怎么回事,主要看这两个公式:
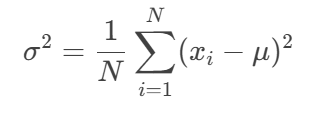
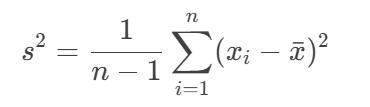
要知道,在数理统计学里面所谓的总体期望和方差往往只是一个概念,或者说是一种理想假设,而关于这个总体到底是个什么,往往只能说我们是永远也无法获得的,我们所有的操作都是在所谓的部分抽样上进行的,因此我们需要明确的知道这里的总体期望是一个假定就已经存在的一个常数(当然,如果用贝叶斯学派的观点来看,这个所谓的总体常数量其实也是一个可以估算的变量)
或者说,第一个公式里面的这个\(u\)是常数,是不需要估计的,不需要计算的;而第二个公式里面的\(\bar{x}\)却是一个计算量,即抽样的估计量(估计均值),其计算公式为\(\bar{x}=\frac{x_1+x_2+...+x_n}{n}\),而这一切都是在第二个公式的\(x_i-\bar{x}\)的时候发生了变化,因为\(x_i\)肯定在\(\bar{x}\)的计算中使用过,于是可以写为\(x_i-\bar{x}=x_i-\frac{x_1+x_2+...+x_n}{n}\),那么我们就能得到:
\(x_i-\bar{x}=x_i-\frac{x_1+x_2+...+x_n}{n}=x_i*\frac{n-1}{n}-\frac{x_1+x_2+...+x_{n-1}}{n}=\frac{n-1}{n}*[x_i-\frac{x_1+x_2+...+x_{n-1}}{n-1}]\)


DeepSeek 问题:
给出自由度损失,分母为n-1的具体的期望计算公式,要求详细步骤
思考:
嗯,用户现在想要详细了解为什么样本方差的无偏估计分母是n-1,特别是具体的期望计算步骤。之前我解释过无偏估计的基本概念和原因,但用户可能需要更深入的数学推导。
首先,我需要回忆一下如何从数学上证明E[s²] = σ²,其中s²用的是n-1。可能用户在学习统计学时遇到了这个公式,但不太明白背后的推导过程,或者老师布置了相关的作业需要详细步骤。
用户可能是学生,或者是刚接触统计学的自学者,对期望的计算不太熟悉。他们可能需要一步步的推导,每个步骤都不能省略,这样才能理解为什么自由度损失会导致分母调整为n-1。
接下来,我应该从定义出发,先写出样本方差的表达式,然后计算它的期望。关键点在于处理样本均值x̄和总体均值μ之间的关系。记得在推导过程中,可能需要用到线性代数中的性质,比如E[x̄] = μ,Var(x̄) = σ²/n,以及样本数据之间的协方差等。
步骤大概是这样的:
-
展开平方项,将(x_i - x̄)^2展开为(x_i - μ + μ - x̄)^2。
-
展开后分成三个部分:Σ(x_i - μ)^2,-2Σ(x_i - μ)(x̄ - μ),和Σ(x̄ - μ)^2。
-
计算每个部分的期望值。
-
将这些期望值组合起来,最终得到E[Σ(x_i - x̄)^2] = (n-1)σ²。
-
因此,当分母为n-1时,样本方差的期望就是σ²,从而证明无偏性。
需要注意的是,这里可能会涉及到样本均值的方差,以及各个x_i之间的独立性,这样才能正确计算期望。可能用户对这部分不太清楚,所以需要详细解释每个步骤的转换,比如为什么E[(x_i - μ)(x_j - μ)]在i≠j时为0,而i=j时为σ²。
此外,可能用户会混淆有偏和无偏估计的应用场景,因此在推导完成后,可以再次强调为什么需要这样的调整,以及在实际应用中需要注意的地方,比如当总体均值已知时,应该使用n而不是n-1。
还要检查是否有步骤跳得太快,导致用户难以跟进。比如,处理交叉项的时候,可能需要更详细地拆分求和项,并解释协方差的计算。另外,使用期望的线性性质,将整体分解为各个部分的期望之和,这也是关键的一步。
最后,确保推导过程清晰,每一步都有合理的数学依据,避免出现过于简略的跳跃,让用户能够一步步理解为什么分母必须是n-1才能得到无偏估计。


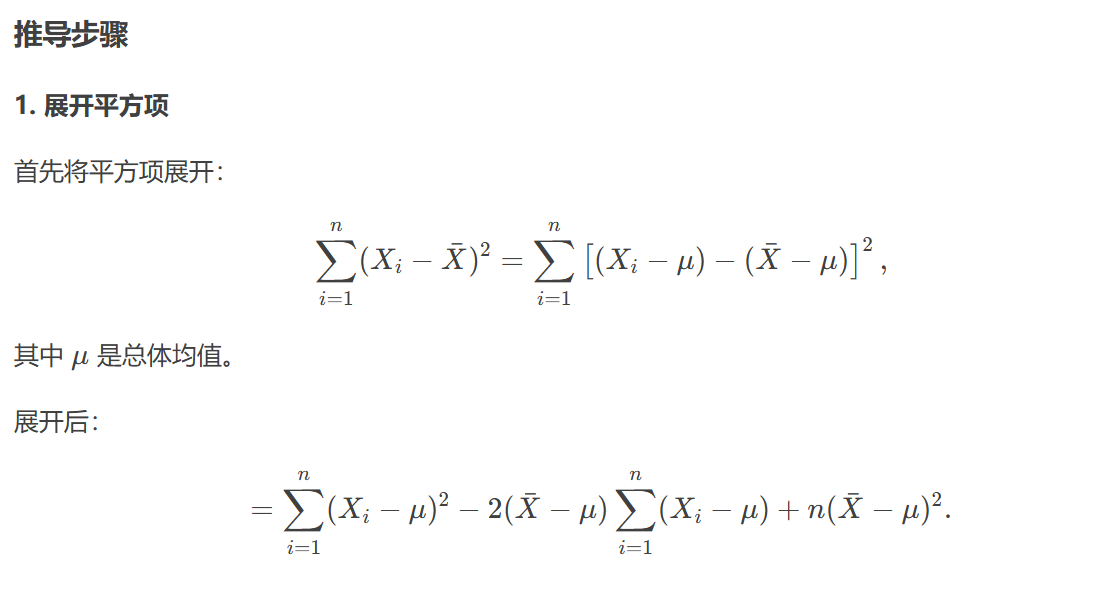
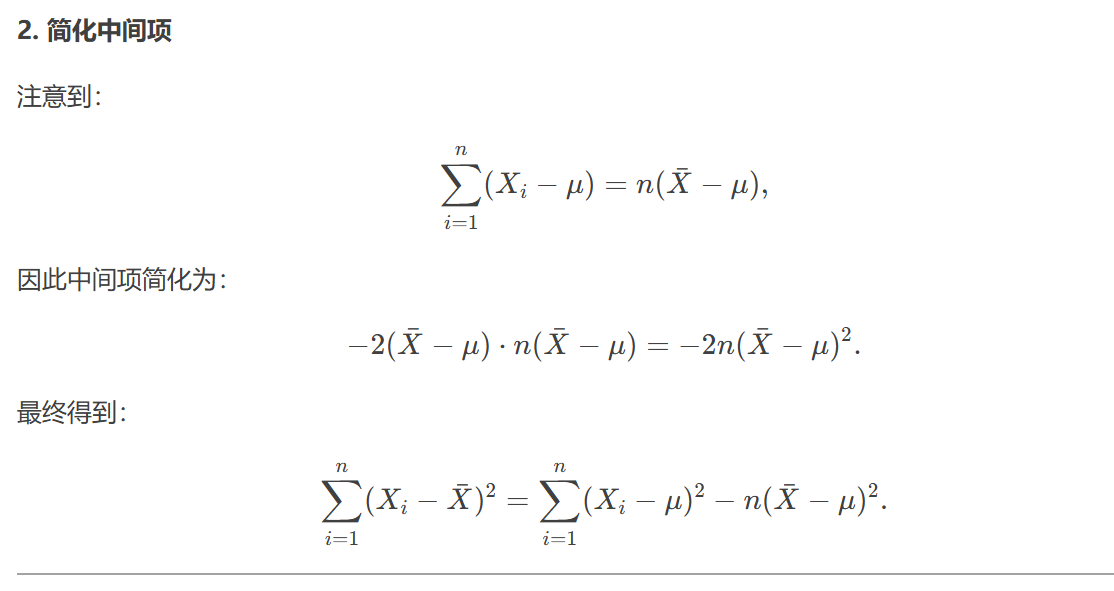

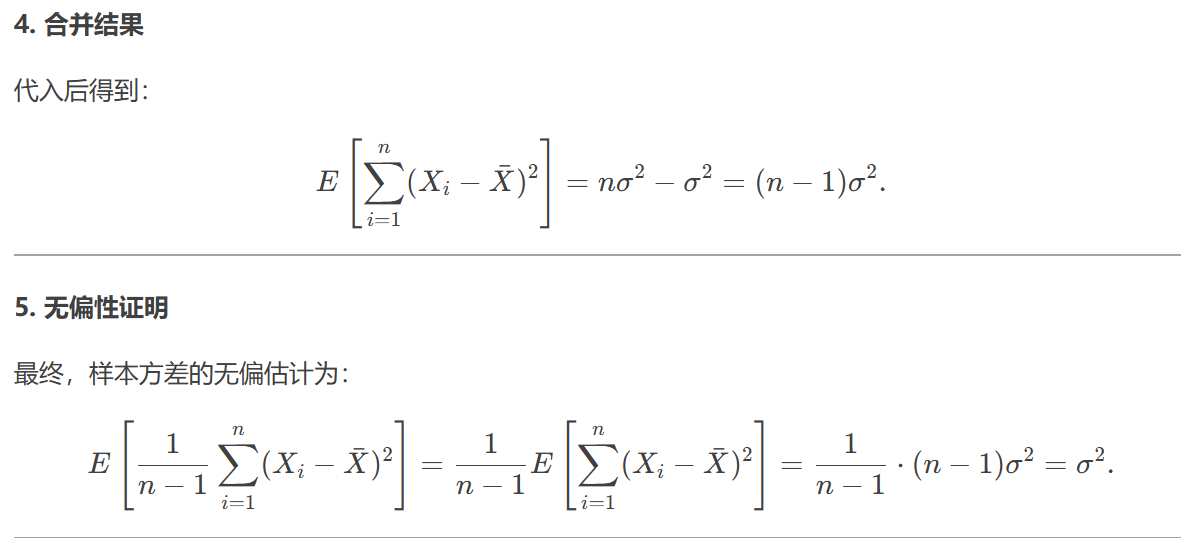

posted on 2025-03-21 15:54 Angry_Panda 阅读(374) 评论(0) 收藏 举报



 浙公网安备 33010602011771号
浙公网安备 33010602011771号