数值优化算法-BFGS

参考：

https://www.cnblogs.com/Leo_wl/p/3367323.html

牛顿法：

使用牛顿法优化函数 f(θ) 最小值时，每次计算获得新的\(θ\)值，即\(θ_{k+1}\)为\(θ_k\)的基础上计算所得。

\(g_k\)为\(f(\theta)\)在\(θ_k\)时雅可比向量，\(H_k\)为\(θ_k\)时Hession矩阵，整体的计算式为：

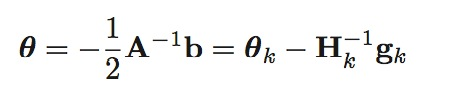
牛顿方法的步骤为:

BFGS算法

Newton算法在计算时需要用到Hessian矩阵H, 计算Hessian矩阵非常费时, 所以研究者提出了很多使用方法来近似Hessian矩阵, 这些方法都称作准牛顿算法, BFGS就是其中的一种, 以其发明者Broyden, Fletcher, Goldfarb和Shanno命名.

BFGS算法使用以下方法来近似Hessian矩阵, Bk≈Hk:

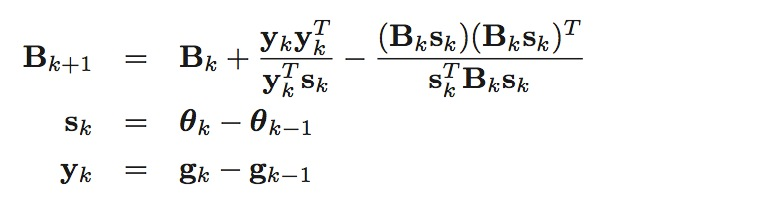
初始时可以取\(B_0=I\)

因为Hessian矩阵的大小为O(D2), 其中D为参数的个数, 所以有时Hessian矩阵会比较大, 可以使用L-BFGS(Limited-memory BFGS)算法来进行优化。

参考文献:

[1]. Machine Learning: A Probabilistic Perspective. p249-p252.

[2]. Wekipedia: L-BFGS

---

给出python版本调用scipy库进行bfgs的计算：

import scipy

def f(arg):
    x1, x2 = arg
    y = x1**2 + x2**2
    return y, [2*x1, 2*x2]

ans = scipy.optimize.fmin_l_bfgs_b(f, (1000, 1000), maxiter=25)
# ans = scipy.optimize.fmin_l_bfgs_b(f, (1000, 1000), maxiter=2)

print(ans)

运行结果：

本文参考：

---

出处1：
源作者：Leo_wl
　　　　
出处：http://www.cnblogs.com/Leo_wl/
　　　　
本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

---