何时使用交叉熵,何时使用KL散度:计算分布差距为啥使用KL散度而不用交叉熵,计算预测差距时为啥使用交叉熵而不用KL散度
问题:
何时使用交叉熵,何时使用KL散度?
计算分布差距为啥使用KL散度而不用交叉熵,计算预测差距时为啥使用交叉熵而不用KL散度
问题很大,答案却很简单。
答案:
- 熵是一种量度,是信息不确定性的量度;
- KL散度不是一种量度,并且不对称,KL(P||Q)一般不等于KL(Q||P);
- 交叉熵不是一种量度;
对于交叉熵不是一种量度进行说明:
如果:
H(P1 || Q1)=0.1
H(P2 || Q2)=0.2
我们是不能说P1分布与Q1分布之间的差距要小于P2分布与Q2分布之间的差距的,因为这两者是不具有比较性的。
只有当
H(P || Q1)=0.1
H(P || Q2)=0.2
时,我们可以说P分布与Q1分布之间的差距要小于P分布与Q2分布之间的差距的,也就是此时才可以说P与Q1的分布差距小于P与Q2的分布的。
需要注意:
H(P || Q1) - H(P || Q2) = KL(P || Q1) - KL(P || Q2)
换句话说,KL散度可以比较两个分布之间的差距,但是无法度量,并且不对称;
同理,交叉熵无法度量两个分布之间的差距,并且无法比较两个分布之间的差距,只有在某个分布固定的前提下才可以比较,而此时在分布差距比较的这一点上交叉熵等价于KL散度。
注意:
KL散度是有方向性的,是不对称的,因此KL(P || Q)是分布P与Q的差距,而不是分布Q与P的差距。因此在下文中使用交叉熵替代KL散度时其也是具有方向性的。
由于交叉熵不具有比较分布差异性的能力,因此在进行计算分布差距和计算预测差距时都是应该使用KL散度而不是交叉熵的。
但是通过KL散度和交叉熵的计算公式可以知道,KL散度的计算复杂度高于交叉熵,同时由于预测差距时真实的分布(label)是已知并且固定的,标签分布用P表示,即分布P已知且固定,也就是说此时 H(P(X)) 是固定不变的,因此的KL散度等价于交叉熵,待优化的分布为Q,因此进行预测差距计算的损失函数使用交叉熵而不是KL散度,就是为了节省计算开销。
也就是说,在P分布已知且固定时,KL(P || Q)等价于H(P || Q),同时由于H(P || Q)计算更快,因此在计算预测差距时损失函数使用交叉熵而不是KL散度,此时待优化的分布为Q。
但是在计算两个分布之间的差距时,分布P是未知的且不固定的,是神经网络的输出值,是待优化的变量,而此时的Q分布往往是采样来的采样数据的分布,并且Q的分布也是随着计算迭代而变量的(不固定的),因此此时是无法使用交叉熵来进行简化计算的,因为此时二者并不等价。
那么既然在预测差距时,我们设定真实标签分布为P,待优化分布为Q,获得KL(P || Q)等价于H(P || Q),从而使用交叉熵代替KL散度,那么我们为啥不在计算分布差距时将待优化分布设置为Q而是设置为P呢?
KL散度虽然可以用来比较两个分布之间的差距,但是其非对称性及其数学定义要求前者分布为真实分布,后者分布为估计分布;也就是说KL散度的基准是前者分布,也就是说P分布要求是真实分布或待优化的目标分布,Q分布可以是拟合分布也可以是采样估计分布。当P分布是固定真实分布时,Q分布为拟合分布;当P分布为待优化的目标分布时,Q分布为采样数据的分布;也就是说KL散度中这个P分布和Q分布是有顺序要求的,重点在于P分布需要为分布比较的基准,或者说P分布要么是固定不变的真实分布,要么是待优化的目标分布。这个问题在计算预测差距时是比较好理解的,难点在于计算分布差距时。
我们假设计算分布差距时,P分布为待优化的目标分布,而Q分布为采样分布,通过计算分布差距实现对P分布的优化(P分布是有参函数,可以当做是一个神经网络)。如果在计算损失函数时我们不使用 KL(P || Q) 而是使用 KL(Q || P),那么每次计算分布差距时的基准则是Q分布,而迭代计算过程中Q分布是不连续变化的,因此这样计算是无法保证计算的收敛和稳定的。换句话说,KL散度的前者分布要求是一个稳定不变的分布或者是一个连续变化的分布,也可以说KL散度中前者分布是优化过程中的target,因此在计算分布差距时前者分布为P,即待优化目标分布,而不能是采样分布。
给出百度本科上的KL散度的定义:


在信息理论中,KL分布是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。典型情况下, P表示数据的真实分布, Q表示数据的理论分布,模型分布,或P的近似分布。
直白的理解,可以认为,KL散度中,P分布为固定不变的,或相对稳定的如待优化目标分布,因为P分布为KL计算中的基准分布。
总结
在本文中,我们介绍了KL散度和交叉熵这两个概念,并比较了它们之间的异同。KL散度用于比较两个概率分布之间的差异,而交叉熵用于衡量模型预测和真实标签之间的差异。尽管它们有一定的联系,但它们在使用和应用上还是有所区别。在机器学习中,KL散度和交叉熵都有着广泛的应用,可以用来评估模型的性能和更新模型参数。
KL散度与交叉熵之间的关系:
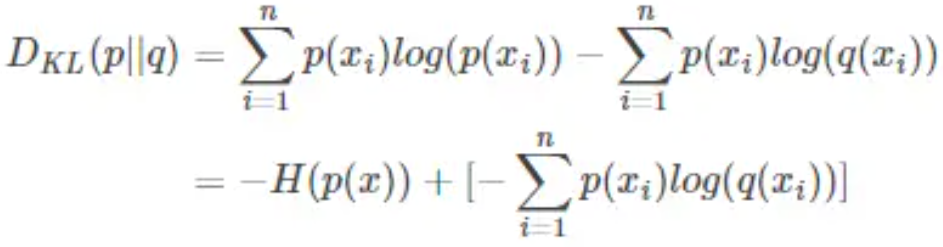
交叉熵:
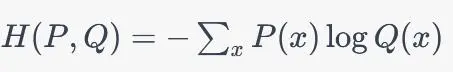
交叉熵具有以下性质:
-
交叉熵是非负的,即CE(P, Q) >= 0,当且仅当P和Q是完全相同的分布时等号成立。
-
交叉熵是不对称的。
-
交叉熵不是度量,因为它不具有三角不等式。
KL散度:
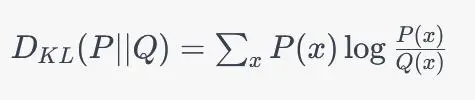
KL散度具有以下性质:
-
KL散度是非负的,即 KLD(P||Q) >= 0,当且仅当P和Q是完全相同的分布时等号成立。
-
KL散度不满足交换律,即 KLD(P||Q) != KLD(Q||P)。
-
KL散度通常不是对称的,即 KLD(P||Q) != KLD(Q||P)。
-
KL散度不是度量,因为它不具有对称性和三角不等式。
在机器学习中,KL散度通常用于比较两个概率分布之间的差异,例如在无监督学习中用于评估生成模型的性能。
参考:
https://baijiahao.baidu.com/s?id=1763841223452070719&wfr=spider&for=pc
posted on 2024-02-12 11:15 Angry_Panda 阅读(562) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号