正定矩阵的生成和判定

正定矩阵的生成和判定：

 

参考：

https://blog.csdn.net/weixin_29732003/article/details/106281708

 

 

 

import numpy as np
from scipy.linalg import orth 

n = 100                      

# M = np.random.randn(n, n)   
# A = np.dot(M.T, M) + 0.01*np.eye(n)
X = np.diag(np.abs(np.random.rand(n))+1)
U = orth(np.random.rand(n, n))
A = np.dot(np.dot(U.T, X), U)  
print("正定矩阵： ", n, "阶")
print(A)

print("判断是否为正定：")
v = np.linalg.eig(A)[0]
print(np.all(v>0))

 

 

 

注意：

该种方式生成的矩阵其过程需要占用大量的计算时间及内存，如果阶数设置为1000以上往往会造成计算机死机或重启，所以上面的方式需要慎用。

 

 

============================================

 

当然我们也可以使用pascal矩阵，该矩阵为正定矩阵，python的生成方式：

from scipy.linalg import invpascal, pascal

p=pascal(100)

 

 

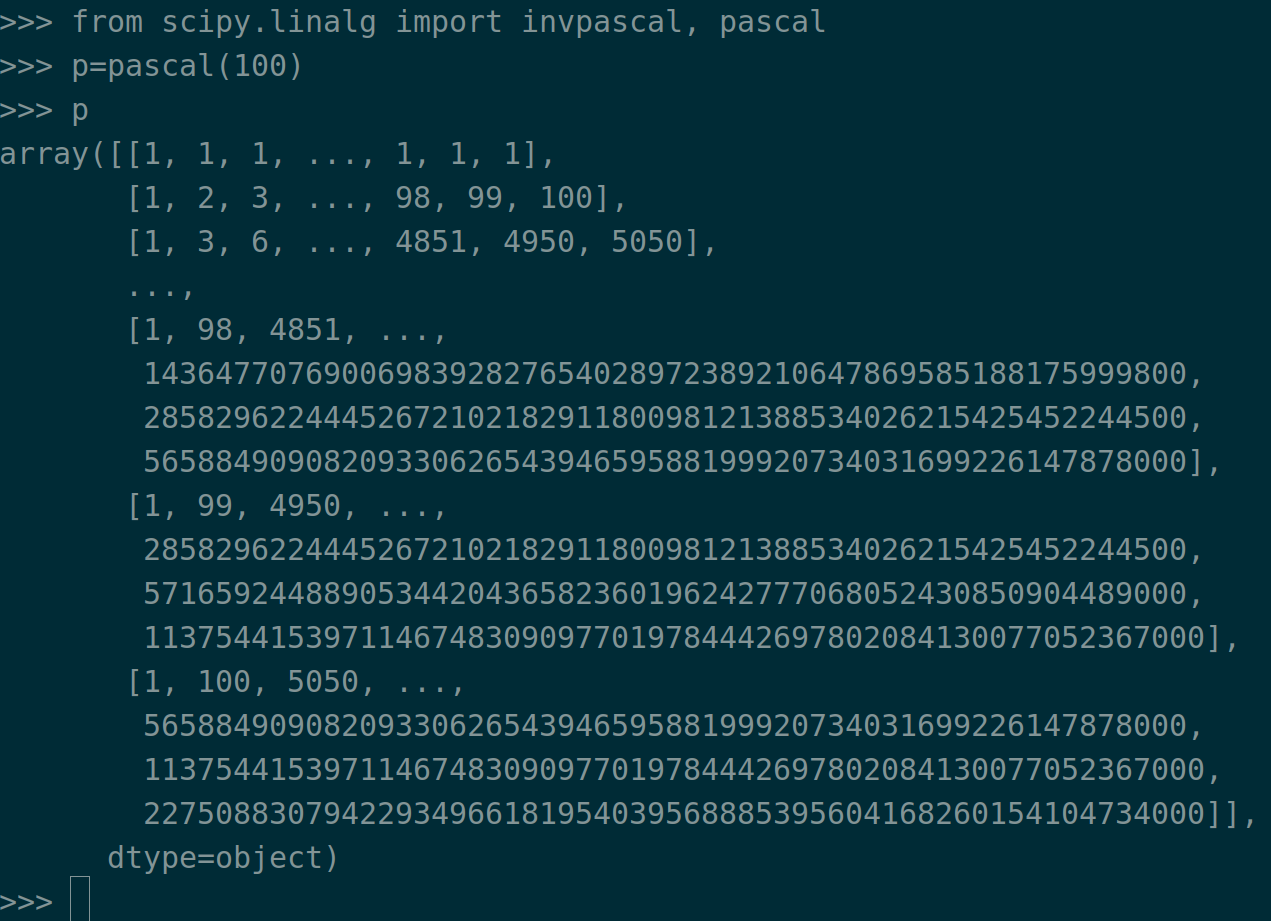
使用该矩阵需要注意的是该矩阵的最大值会变得特别大，因此该矩阵的生成对实际计算中使用意义并不大。

 

 

=======================================