【P1601 A+B Problem（高精）】零基础入门【高精度算法】

 

一、为什么要用高精度    

 

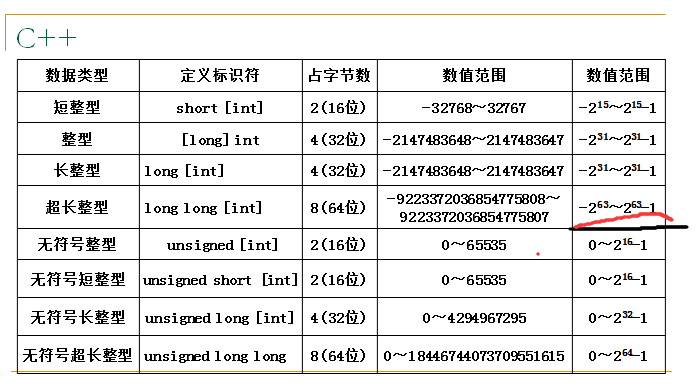
根据上表，我们知道 long long [int]的数位比较大  大约是9x10^18  

 对于简单的  a+b 

 

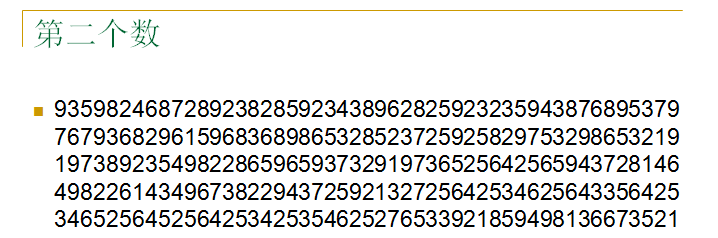
 数位远远 超过20位以上，因此long long[int]不能满足输入、存储 和运算要求，所以必须要学习 高精度运算。

二、数据的存储

 

 

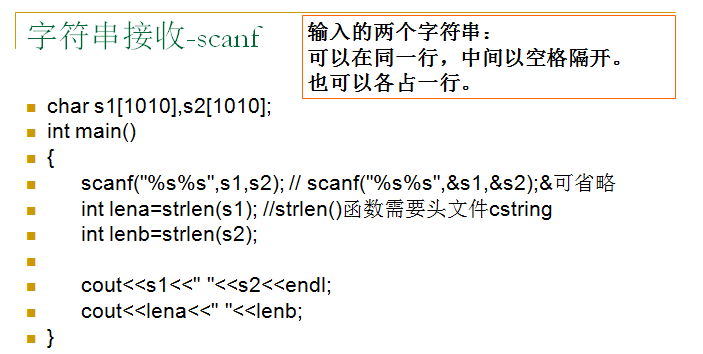
三 、课本181页 例1.1  和洛谷【p1601】高精度加法

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int a[502],b[502],c[502];
int main()
{
   char a1[502],b1[502];
   int lena,lenb,lenc,i,x;
   //gets(a1);      //第5版课本 gets()读入，在洛谷上AC不了，原因 gets()读入处理 回车处理不了。         
   //gets(b1);
   scanf("%s",a1);  //推荐做题用scanf()读入字符串。 
   scanf("%s",b1); 
   lena=strlen(a1);
   lenb=strlen(b1);
   for(i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48;
   for(i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48;
   lenc=1;
   x=0;
   while(lenc<=lena||lenc<=lenb)   //满足条件不进位，如果lenc>的话，加法结束只是   跳转到25行需要进位。 
    { 
      c[lenc]=a[lenc]+b[lenc]+x;
      x=c[lenc]/10;
      c[lenc]=c[lenc]%10;     //超过10 的话保留个位。
      lenc++;                //接着处理第二位 
    }
    c[lenc]=x; 
    if(c[lenc]==0) lenc--;   //最高位不能为0
    for(i=lenc;i>=1;i--)  cout<<c[i];
return 0;
}