【 P1090 合并果子】堆模解题/queue优先队列解题/哈夫曼树模板题/贪心求解未完善

洛谷地址：https://www.luogu.org/problemnew/show/P1090

白书第五版：448页

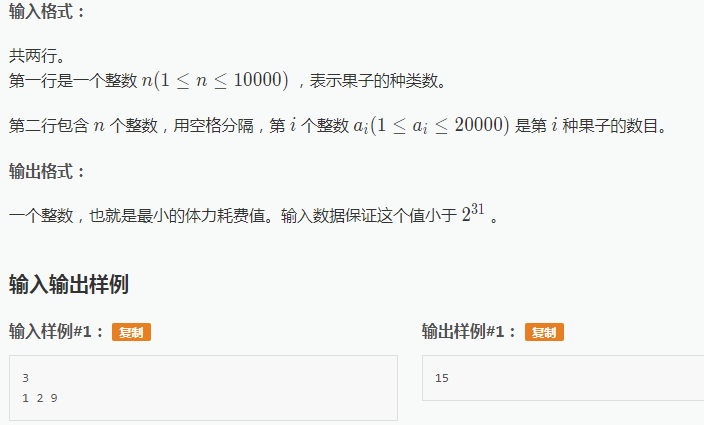
（1）分析图

 

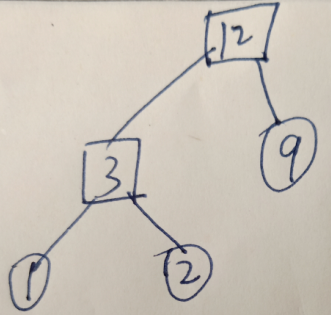
堆策略：3+12=15   为最小合并力气

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int heap_size,n;
int heap[30001];

void put(int d)
{  //入堆， 完全二叉树最后一个元素入堆后并维护堆 
    int now,next;
    heap[++heap_size]=d;
    now=heap_size;
    while(now>1)
     {   next=now/2;   //next是父节点 
         if(heap[now]>=heap[next]) break;    //小根堆
        swap(heap[now],heap[next]);
        now=next;     
     } 
}

int  get( )
{  //出堆 
    int now,next,res;
    res=heap[1]; //第一个出堆 
    heap[1]= heap[heap_size--]; //最后面一个调整到第一个
    now=1;
    while(now*2<=heap_size)
     { next=now*2;
       if(next<heap_size&&heap[next+1]<heap[next]) next++; //next标记最小的
       if(heap[now]<=heap[next])  break; //维护小根堆
       else swap(heap[now],heap[next]);
       now=next; 
     }
     return res;  //弹出堆顶
}
void  work()
{
    int i,x,y,ans=0;
    cin>>n;
    for(i=1;i<=n;i++)
     {cin>>x; put(x);}  //输入的元素入堆，建立小根堆
     
     for(i=1;i<n;i++)  // n个数 合并n-1次 
       {                      
           x=get();  y=get();      //i=1   x=1,y=2 ans=3   3入堆 
           ans+=x+y;               //i=2   x=3,y=9 ans=3+3+9=15  15入堆，结束循环 
           put(x+y);
        }  
     cout<<ans<<endl;
}
int main()
{
    work();
    return 0;
 } 

 【优先队列解题】https://www.cnblogs.com/xxas2015/articles/10112206.html

哈夫曼树：带权路径长度之和为最小力气（所有叶子权值x路径长度，之和）：   1x2+2x2+9x1 =15.

（2）知识扩展

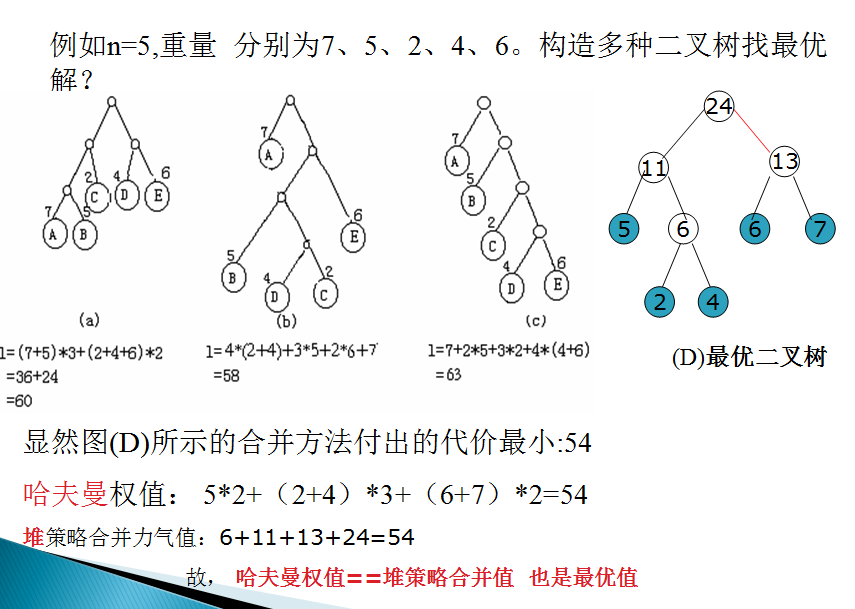
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <climits> 
using namespace std;
int n, m;
struct Node
{
    int data,prt,lch,rch,dep;
};
Node tree[10005];  
int i,j,k;
const int oo = INT_MAX;
int min1(int h)  //选择前h结点中父指针为0且权值最小的2个结点
{
    int m1 = oo,p,i;
    for(p = 1;p <= h;p++)
    {
        if(tree[p].prt == 0 && m1 > tree[p].data)
        {
            i = p;
            m1 = tree[p].data;
        }
    }
    return i;
}
void hufm()
{   //建立一棵树的过程 
    for(k = n + 1;k <= m;k++)
    {
        i = min1(k - 1);
        tree[i].prt = k;
        tree[k].lch = i;
        j=min1(k - 1);
        tree[j].prt = k;
        tree[k].rch = j;        
        tree[k].data = tree[i].data + tree[j].data;
    }
}

int main()
{
    scanf("%d", &n);
    m=2*n-1;   //n个叶子，节点总数为  2n-1 
    for(i = 1; i <= n; i++)
        scanf("%d",&tree[i].data);
    hufm();
    tree[m].dep = 0;                //先记录最m层，最底层 
    for(i = m - 1; i >= 1; i--)      //从最底层到 最上层依次计算深度 
        tree[i].dep = tree[tree[i].prt].dep + 1;  //当前深度等于父亲深度加1 
    int ans=0;
    for(i = 1; i <= n; i++)       //计算n个节点的带权路径之和 
        ans += tree[i].data * tree[i].dep;
    printf("%d\n", ans);
    return 0;
}

 

 

洛谷提交来看： 总结  （1）堆 AC了，因为堆优化nlong(n)        （2）哈夫曼提交得到50分，因为哈夫曼是 n*nd的。