最小生成树算法实现与分析:Prim 算法,Kruskal 算法;
连通图:无向图G中,若从顶点i到顶点j有路径相连,则称i,j是连通的;如果G是有向图,那么连接i和j的路径中所有的边都必须同向;如果图中任意两点之间都是连通的,那么图被称作连通图。
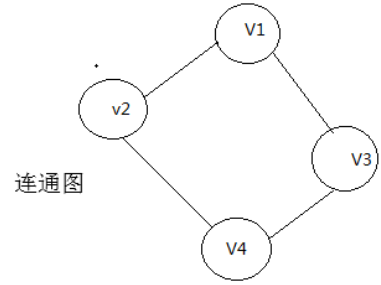
强连通图:有向图G中,对于任意的两个点之间x,y,都存在x到y的路径,为强连通图;
弱连通图:将有向图的所有的有向边替换为无向边,所得到的图称为原图的基图。如果一个有向图的基图是连通图,则有向图是若连通图;
单向连通:G=V,E;是有向图,对于任意u,v属于V,从u到达v或者v可达u,则称G为单向连通图;
连通分量:无向图的一个极大连通图子图称为G的一个连通分量;连通图只有一个连通分量;
极大连通子图:(无向图)
- 连通图只有一个极大连通子图,就是它本身;
- 非连通图有多个极大连通子图(非连通图的极大连通子图叫做连通分量,每个分量都是一个连通图);
- 极大连通子图中,加入任何一个不在图点集中的点都会导致它不再连通;
- 下图为非连通图,图中有两个极大连通子图(连通分量):
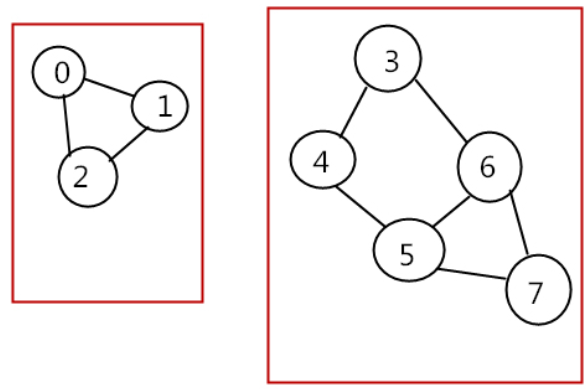
极小连通子图:(无向图)
- 一个连通图的生成树是该连通图的极小连通子图;(同一个连通图有不同的生成树,所以生成树不是唯一的,最小生成树是唯一的);
- 极小连通子图是个连通图;
- 极小连通子图中,顶点个数为n, 则边的个数为n-1;
- 如果在生成树上添加一条边,一定会构成一个环;
- 极小连通子图的每条边都不可少,如果去掉一条边,则变成两个连通分量;
- 生成树:一个连通图的最小连通子图,无回路;
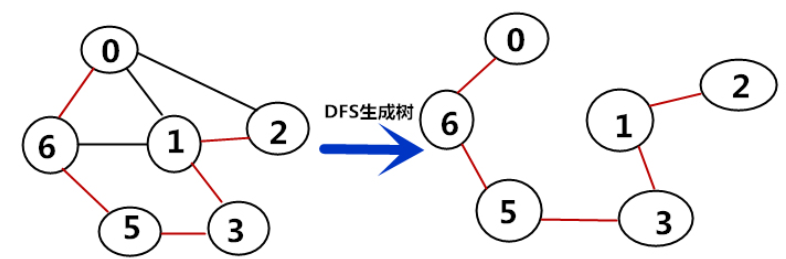
极大强连通子图:(有向图)
- 强连接图的极大强链接图为其本身;唯一;
- 非强连接图有多个极大强连通子图。非强连通图的极大连通子图叫做强连通分量;
最小生成树:一个有n个节点的连通图的生成树是原图的极小连通子图,且包含了原图中的所有n个节点,并且有保持图连通的最少的边;最少生成树可以使用Kruskal算法和Prim算法求出;
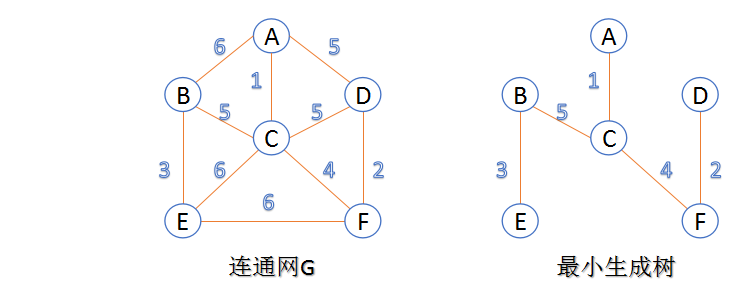
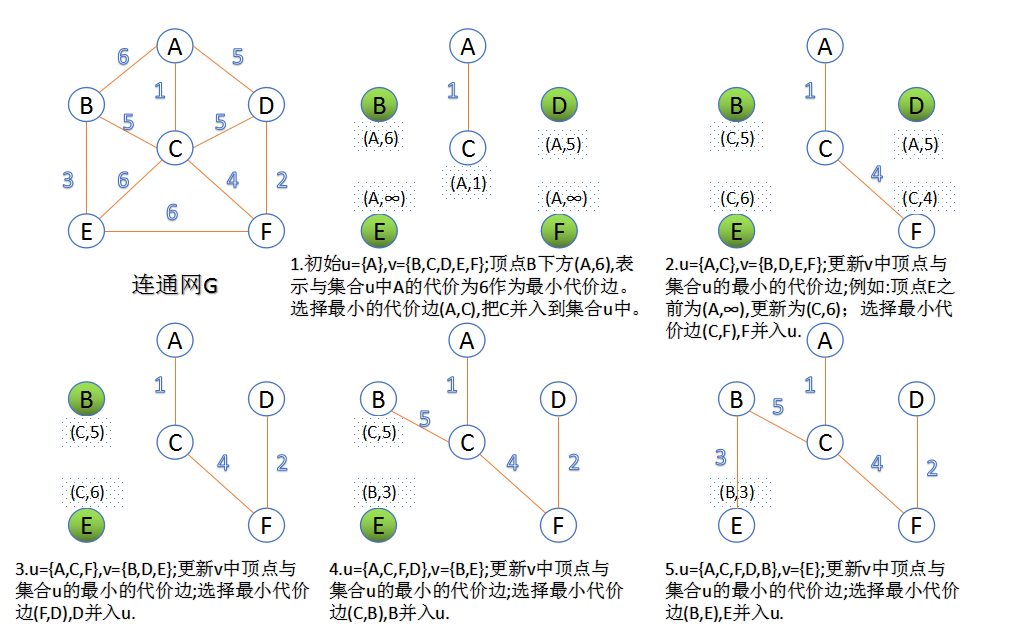
Prim算法:此算法可以称为加点法,使用贪心思想进行求解,Vnew Vold-new 之间,代价最小的边对应的点,加入到Vnew之中;算法从任意一节点开始,知道Vnew中包含所有的点;
- 图中所有顶点集合V, 初始结合Vnew = {s}, Vold-new = V-Vnew;
- 在两个集合Vnew和Vold-new 组成的边中,选择代价最小的边(vnew, vold-new),加入到生成树;并把vold-new加入到Vnew之中;
- 重复上述步骤,直到Vnew包含所有的点;
- 证明:假设权值最小的边不在最小生成树中,此时将权值最小的边加入生成树中,必然会构成一个回路,去掉回路中权值最大的边,构成一个新的最小生成树,这时权值最小的边在最小生成树中,与原有假设构成矛盾,所以权值最小的边一定在最小生成树中;所以prim每次选入权值最小的边的点加入的策略是正确的。
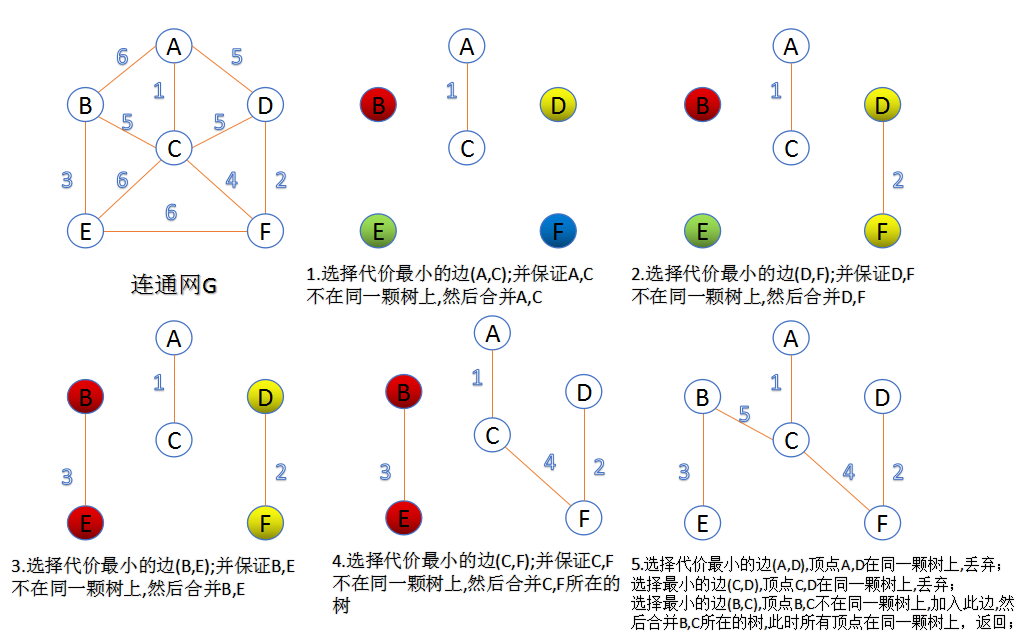
Kruskal算法:此算法可称为加边法;初始生成树边数为0,每次就选择一条满足条件的最小代价的边,加入到生成树的边集合中;
- 把图中的所有边按代价从小到大排序;
- 把图中的n个顶点,看成独立的n棵树组成的森林;
- 按照权值从小到大选择边,所选边的顶点u,v应该属于两颗不同的树;则成为最小生成树的一条边,并将这两颗树合并为一棵树;
- 重复上述操作,直到当前边集合中包括n-1课树为止;
算法实现参考:https://github.com/yaowenxu/codes/tree/master/最小生成树算法
保持更新,转载请注明出处;更多内容请关注cnblogs.com/xuyaowen;
参考链接:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号