【翻译】理解 LSTM 及其图示
本文翻译自 Shi Yan 的博文 Understanding LSTM and its diagrams,原文阐释了作者对 Christopher Olah 博文 Understanding LSTM Networks 更加通俗的理解。
Understanding LSTM Networks 中译:【翻译】理解 LSTM 网络
理解 LSTM 及其图示
我不擅长解释 LSTM,写下这段文字是为了我个人记忆方便。我认为 Christopher Olah 的那篇博文是关于 LSTM 最棒的资料。如果想要学习 LSTM 的话,请移步到原始的文章链接。(我会在这里画一些更漂亮的图示)
尽管我们不知道大脑的运行机制,但我们依然能够感觉到它应该有一个逻辑单元和一个记忆单元。我们基于推理和经验得到的这个结论,就像电脑一样,我们也有逻辑单元、CPU 和 GPU,以及内存。
但是,当你观察一个神经网络的时候,它工作起来就像一个黑箱。你从一端出入,再从另一端得到输出。整个决策过程几乎完全取决于当前的输入。
我觉得,说神经网络完全没有记忆是不恰当的。无论怎样,学习得到的权重可以看作是训练数据的一种记忆。但是这种记忆更加静态。有些时候我们需要为后面的使用记住一些输入。这种例子很多,比如股票市场。为了做出好的投资决策,我们至少要从一个时间窗口回溯股票数据。
若要让神经网络接受时间序列数据,最简单的方法就是将若干神经网络连接在一起。每个神经网络只处理一步。你需要向神经网络提供一个时间窗口上所有步的数据,而不是单一步。
许多时候,你处理的数据具有周期模式。举个简单的例子,你需要预测圣诞树的销量。这是件季节性很强的事,每年只有一个高峰出现。一个好的预测策略是回溯一年前的数据。对于这类问题,你需要包含很早以前的数据,或者很强的记忆。你需要知道那哪些有价值的数据需要记住,哪些没用数据要忘记。
理论上,简单连接的神经网络称为递归神经网络,是可以工作的。但实践中面临两个难题:梯度消失和梯度爆炸,这会使神经网络无法使用。
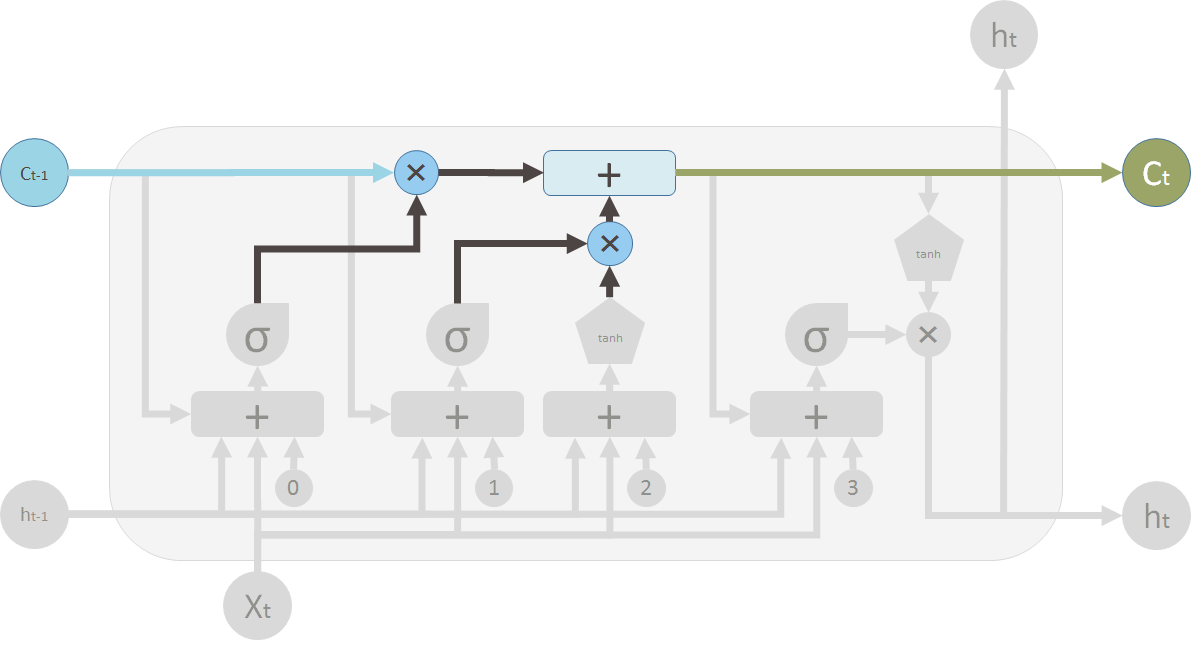
后来出现的 LSTM(长短期记忆网络)通过引入记忆单元(即神经网络的细胞)来解决上述问题。LSTM 模块的图示如下:
I'm not better at explaining LSTM, I want to write this down as a way to remember it myself. I think the above blog post written by Christopher Olah is the best LSTM material you would find. Please visit the original link if you want to learn LSTM. (But I did create some nice diagrams.)
Although we don't know how brain functions yet, we have the feeling that it must have a logic unit and a memory unit. We make decisions by reasoning and by experience. So do computers, we have the logic units, CPUs and GPUs and we also have memories.
But when you look at a neural network, it functions like a black box. You feed in some inputs from one side, you receive some outputs from the other side. The decision it makes is mostly based on the current inputs.
I think it's unfair to say that neural network has no memory at all. After all, those learnt weights are some kind of memory of the training data. But this memory is more static. Sometimes we want to remember an input for later use. There are many examples of such a situation, such as the stock market. To make a good investment judgement, we have to at least look at the stock data from a time window.
The naive way to let neural network accept a time series data is connecting several neural networks together. Each of the neural networks handles one time step. Instead of feeding the data at each individual time step, you provide data at all time steps within a window, or a context, to the neural network.
A lot of times, you need to process data that has periodic patterns. As a silly example, suppose you want to predict christmas tree sales. This is a very seasonal thing and likely to peak only once a year. So a good strategy to predict christmas tree sale is looking at the data from exactly a year back. For this kind of problems, you either need to have a big context to include ancient data points, or you have a good memory. You know what data is valuable to remember for later use and what needs to be forgotten when it is useless.
Theoretically the naively connected neural network, so called recurrent neural network, can work. But in practice, it suffers from two problems: vanishing gradient and exploding gradient, which make it unusable.
Then later, LSTM (long short term memory) was invented to solve this issue by explicitly introducing a memory unit, called the cell into the network. This is the diagram of a LSTM building block.
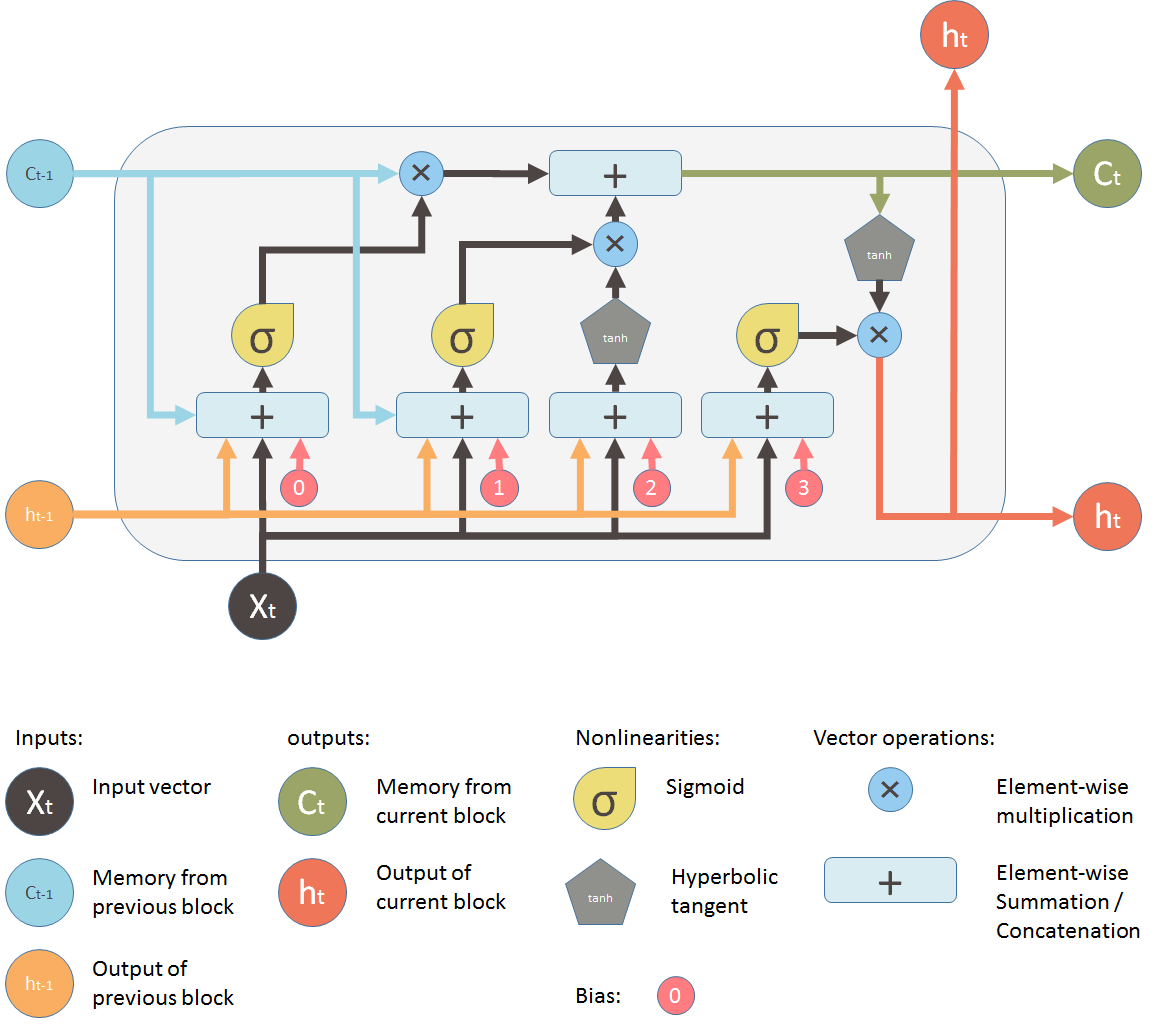
初看起来非常复杂。让我们忽略中间部分,只看单元的输入和输出。网络有三个输入,\(X_t\) 是当前的输入;\(h_{t-1}\) 是上一个 LSTM 单元的输出;\(C_{t-1}\) 是我认为最重要的输入——上一个 LSTM 单元的“记忆”。\(h_t\) 是当前网络的输出,\(C_t\) 是当前单元的记忆。
所以,一个单元接收当前的输入、前一个输出和前一个记忆做出决策,并且产生新的输出,更新记忆。
At a first sight, this looks intimidating. Let's ignore the internals, but only look at the inputs and outputs of the unit. The network takes three inputs. \(X_t\) is the input of the current time step. \(h_{t-1}\) is the output from the previous LSTM unit and \(C_{t-1}\) is the “memory” of the previous unit, which I think is the most important input. As for outputs, \(h_t\) is the output of the current network. \(C_t\) is the memory of the current unit.
Therefore, this single unit makes decision by considering the current input, previous output and previous memory. And it generates a new output and alters its memory.


中间部分记忆 \(C_t\) 产生变化的方式非常类似于从管道中导出水流。把记忆想象成管道中的水流。你想要改变记忆流,而这种改变有两个阀门控制。
第一个阀门是遗忘阀门。如果你关掉阀门,旧的记忆不会被保留;如果完全打开,旧的记忆就会完全通过。
第二个阀门是新记忆阀门。新的记忆会通过一个 T 形连接,并于同旧的记忆混合。第二个阀门决定要通过多少新的记忆。
The way its internal memory \(C_t\) changes is pretty similar to piping water through a pipe. Assuming the memory is water, it flows into a pipe. You want to change this memory flow along the way and this change is controlled by two valves.
The first valve is called the forget valve. If you shut it, no old memory will be kept. If you fully open this valve, all old memory will pass through.
The second valve is the new memory valve. New memory will come in through a T shaped joint like above and merge with the old memory. Exactly how much new memory should come in is controlled by the second valve.
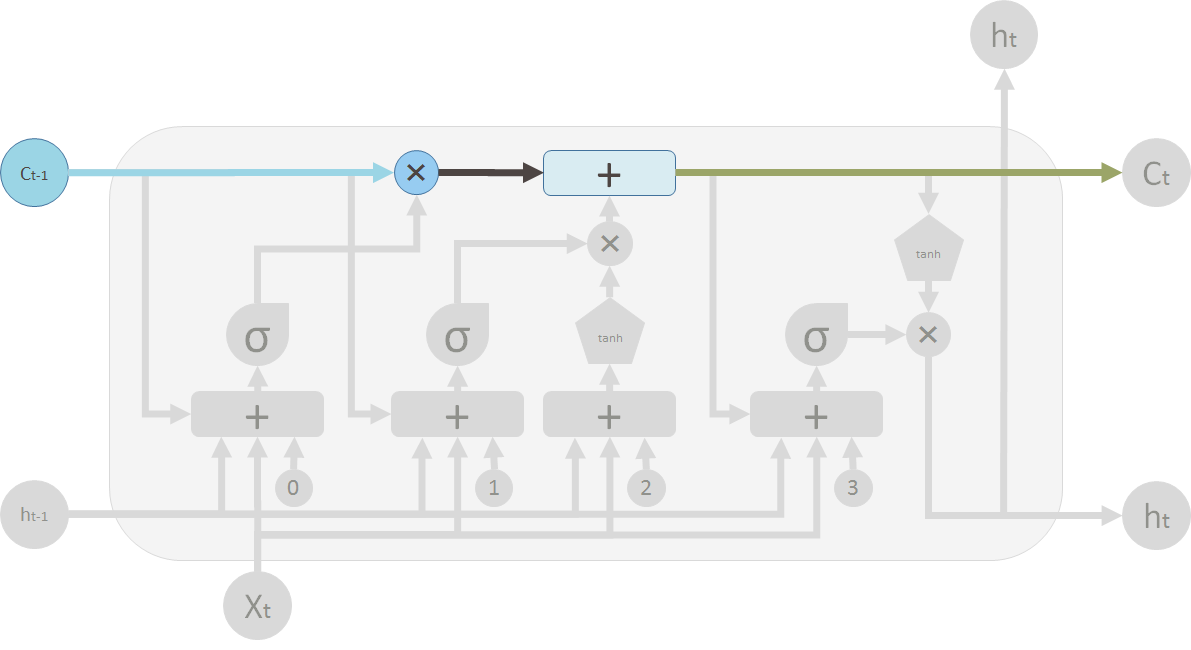
在图示中,顶部的管道是记忆管道。输入是旧的记忆(以向量的形式)。通过的第一个 \(\times\) 是遗忘阀门,事实上这是一个逐点乘法运算。如果你将旧的记忆 \(C_{t-1}\) 与一个接近 0 的向量相乘,这意味着你想要忘记绝大部分记忆。如果你让遗忘阀门等于 1 ,旧的记忆就会完全通过。
记忆流通过的第二个运算是加法运算符 \(+\),即逐点相加,它的功能类似 T 形连接。新旧记忆通过这个运算混合。另一个阀门控制多少新的记忆来和旧的记忆混合,就是 \(+\) 下面的 \(\times\)。
两步运算之后,你就将旧的记忆 \(C_{t-1}\) 变成了新的记忆 \(C_t\)。
On the LSTM diagram, the top “pipe” is the memory pipe. The input is the old memory (a vector). The first cross \(\times\) it passes through is the forget valve. It is actually an element-wise multiplication operation. So if you multiply the old memory \(C_{t-1}\) with a vector that is close to 0, that means you want to forget most of the old memory. You let the old memory goes through, if your forget valve equals 1.
Then the second operation the memory flow will go through is this + operator. This operator means piece-wise summation. It resembles the T shape joint pipe. New memory and the old memory will merge by this operation. How much new memory should be added to the old memory is controlled by another valve, the \(\times\) below the + sign.
After these two operations, you have the old memory \(C_{t-1}\) changed to the new memory \(C_t\).
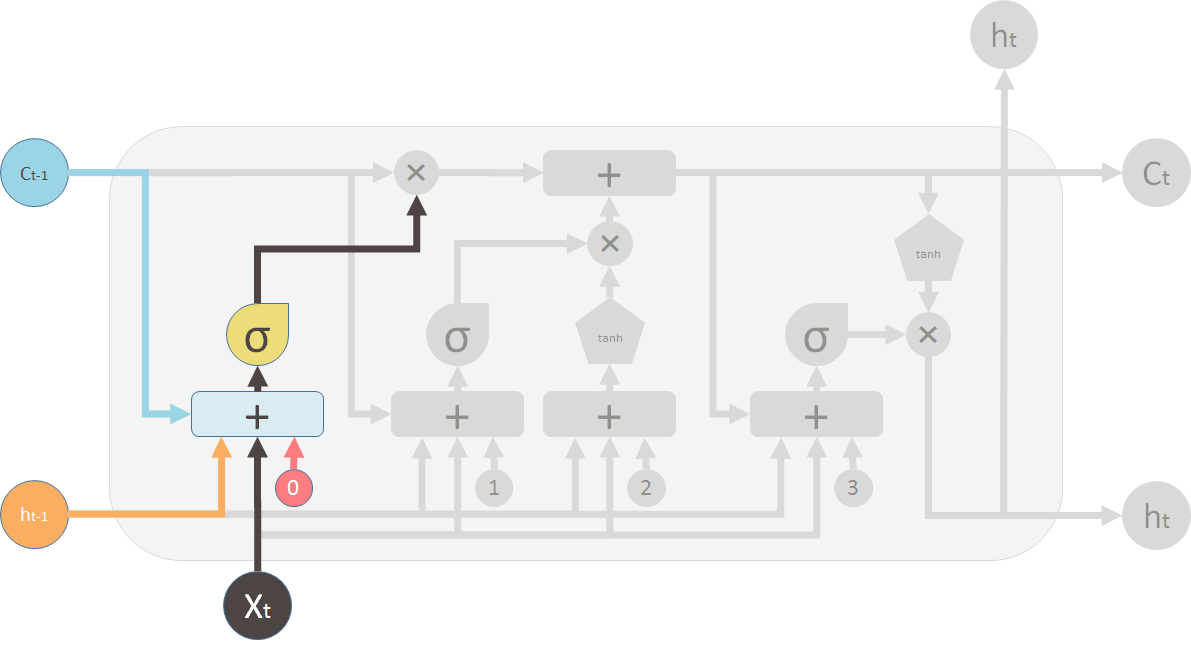
现在让我们看看阀门。第一个阀门称为遗忘阀门。它由一个单层神经网络控制。它的输入是 \(h_{t-1}\)(前一个 LSTM 模块的输出)、\(X_t\)(当前 LSTM 模块的输入)、\(C_{t-1}\)(前一个模块的记忆)和最终的偏移向量 \(b_0\)。这个神经网络有一个 S 形激活函数,它的输出向量是遗忘阀门,用来和旧的记忆 \(C_{t-1}\) 做逐点乘法。
Now lets look at the valves. The first one is called the forget valve. It is controlled by a simple one layer neural network. The inputs of the neural network is \(h_{t-1}\), the output of the previous LSTM block, \(X_t\), the input for the current LSTM block, \(C_{t-1}\), the memory of the previous block and finally a bias vector \(b_0\). This neural network has a sigmoid function as activation, and it's output vector is the forget valve, which will applied to the old memory \(C_{t-1}\) by element-wise multiplication.
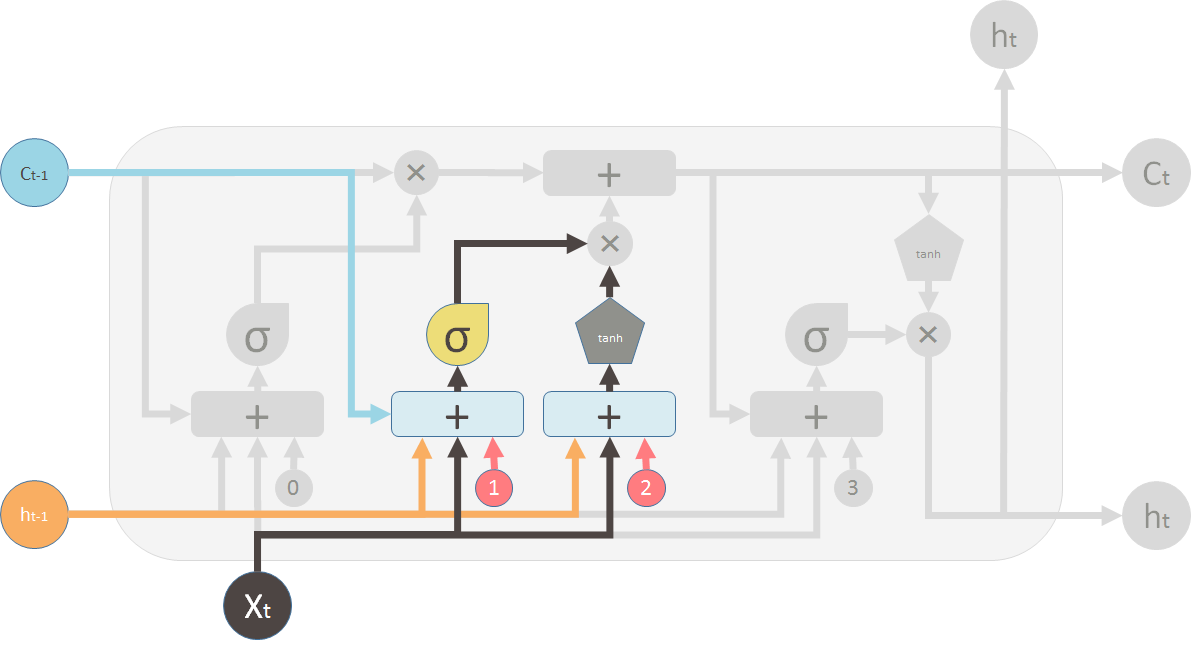
第二个阀门称为新记忆阀门。它也是一个单层神经网络,接收的输入和遗忘阀门一样。这个阀门用来控制多少新的记忆用来影响旧的记忆。
但是,新的记忆却由另一个神经网络产生。这也是一个单层神经网络,但是用 tanh 作为激活函数。这个神经网络的输出将会和新记忆阀门的输出做逐点乘法,然后和旧的记忆相加产生新的记忆。
Now the second valve is called the new memory valve. Again, it is a one layer simple neural network that takes the same inputs as the forget valve. This valve controls how much the new memory should influence the old memory.
The new memory itself, however is generated by another neural network. It is also a one layer network, but uses tanh as the activation function. The output of this network will element-wise multiple the new memory valve, and add to the old memory to form the new memory.
两个 \(\times\) 是遗忘阀门和新记忆阀门。
These two \(\times\) signs are the forget valve and the new memory valve.

最终,我们需要产生这个 LSTM 单元的输出。这一步有一个输出阀门,它被新的记忆、前一个输出 \(h_{t-1}\)、当前输入 \(X_t\) 和偏移向量共同控制。这个阀门控制向下一个 LSTM 单元输出多少新的记忆。
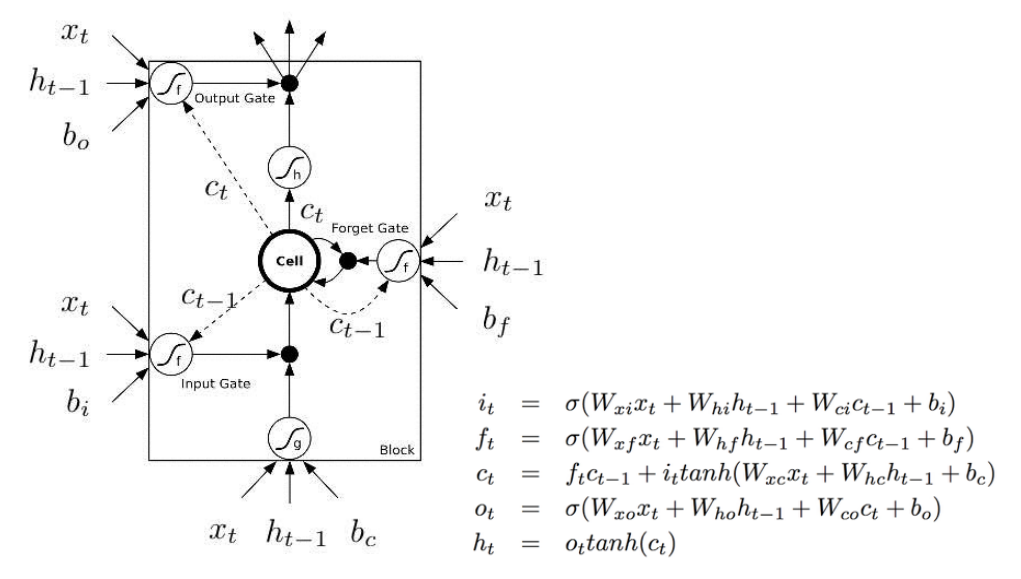
前一个图是受到 Christopher 博文的启发。但是通常情况下,你会看到下面的图。两幅图之间的主要差异是后一个图没有将记忆单元 C 作为 LSTM 单元的输入。相反,它把它(记忆单元)内化成了“细胞”。
我喜欢 Christopher 的图,它清晰地展示了记忆 C 如何从前一个单元传递到下一个单元。在下面的图中,你不能轻易的发现 \(C_{t-1}\) 来自上一个单元,以及 \(C_t\) 是输出的一部分。
我不喜欢下面的图的第二个原因是,单元中的计算是有顺序的,但是你不能直接从图中看出来。例如,为了计算单元的输出,你需要有新的记忆 \(C_t\)。因此,第一步应该是计算 \(C_t\)。
下面的图试图通过实线和虚线来强调这种“延迟”或“顺序”。虚线是开始就已经就绪的旧的记忆。实线是新的记忆。计算要求新的记忆要等待 \(C_t\) 的就绪。
And finally, we need to generate the output for this LSTM unit. This step has an output valve that is controlled by the new memory, the previous output \(h_{t-1}\), the input \(X_t\) and a bias vector. This valve controls how much new memory should output to the next LSTM unit.
The above diagram is inspired by Christopher's blog post. But most of the time, you will see a diagram like below. The major difference between the two variations is that the following diagram doesn't treat the memory unit C as an input to the unit. Instead, it treats it as an internal thing “Cell”.
I like the Christopher's diagram, in that it explicitly shows how this memory C gets passed from the previous unit to the next. But in the following image, you can't easily see that \(C_{t-1}\) is actually from the previous unit, and \(C_t\) is part of the output.
The second reason I don't like the following diagram is that the computation you perform within the unit should be ordered, but you can't see it clearly from the following diagram. For example to calculate the output of this unit, you need to have \(C_t\), the new memory ready. Therefore, the first step should be evaluating \(C_t\).
The following diagram tries to represent this “delay” or “order” with dash lines and solid lines (there are errors in this picture). Dash lines means the old memory, which is available at the beginning. Some solid lines means the new memory. Operations require the new memory have to wait until \(C_t\) is available.
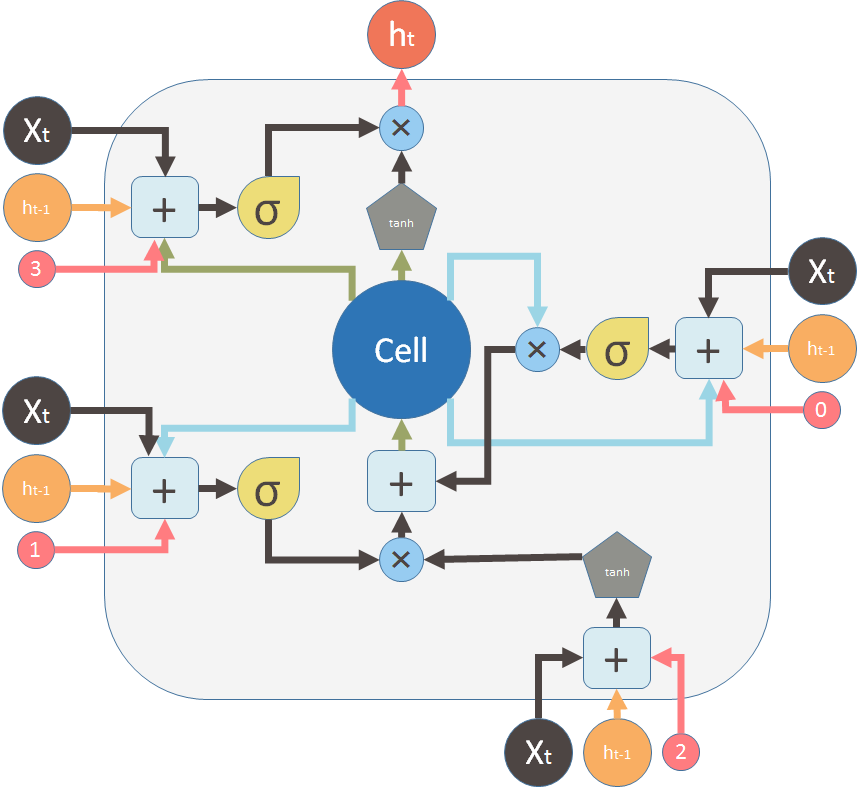
但是这两幅图是一样的。这里,我用和第一幅图相同的符号和颜色重画上面的图:
But these two diagrams are essentially the same. Here, I want to use the same symbols and colors of the first diagram to redraw the above diagram:
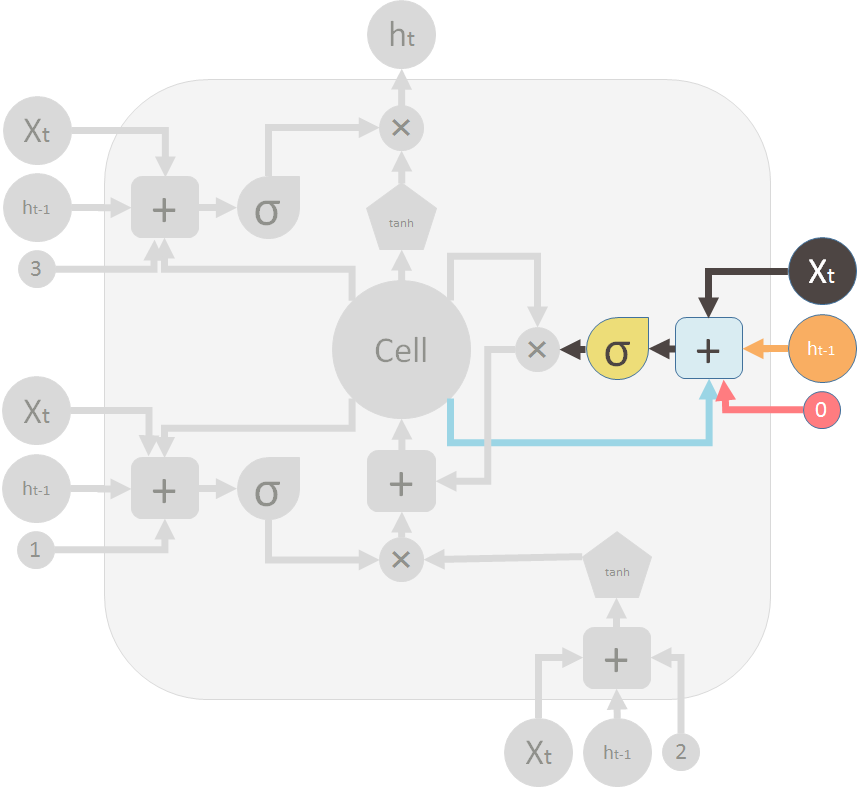
这是遗忘门(阀门)关闭旧的记忆。
This is the forget gate (valve) that shuts the old memory:
这是新记忆阀门和新的记忆:
This is the new memory valve and the new memory:
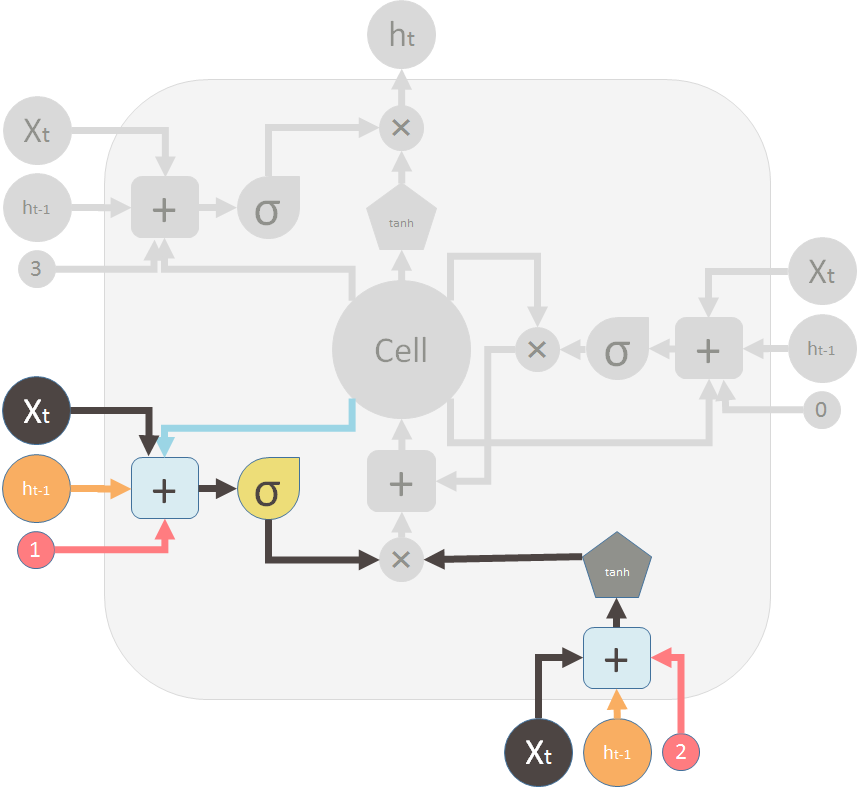
这是两个阀门和逐点加法将新旧记忆混合以产生 \(C_t\)(绿色的,在大 “Cell” 后面)。
These are the two valves and the element-wise summation to merge the old memory and the new memory to form \(C_t\) (in green, flows back to the big “Cell”):
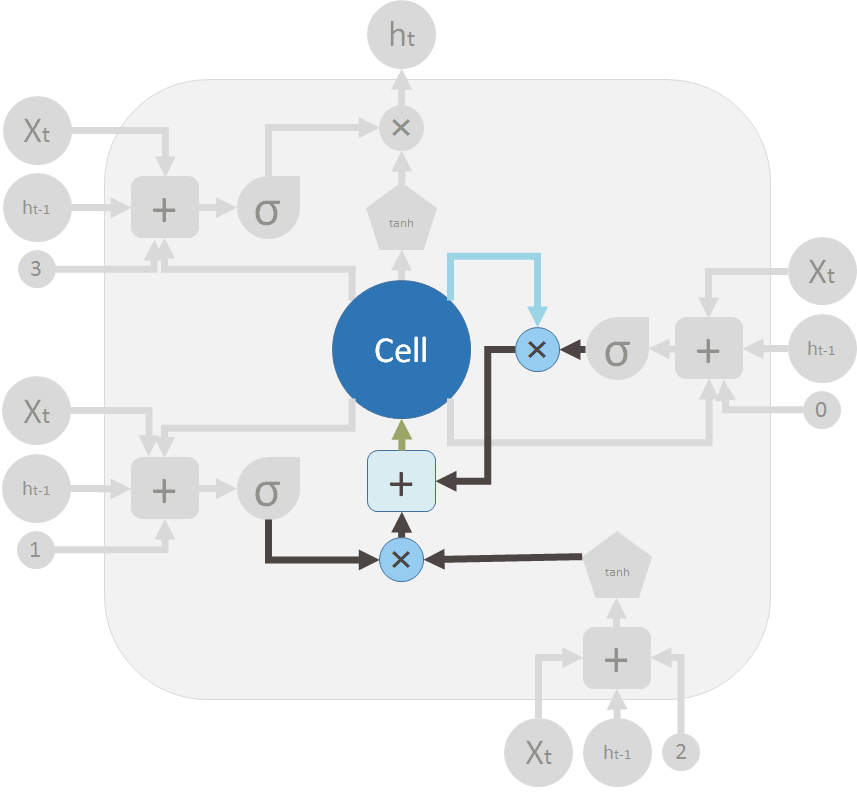
这是输出阀门和 LSTM 单元的输出。
This is the output valve and output of the LSTM unit:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号