基于 Keras 用 LSTM 网络做时间序列预测
本文主要参考了 Jason Brownlee 的博文 Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras
原文使用 python 实现模型,这里是用 R
基于 Keras 用 LSTM 网络做时间序列预测
时间序列预测是一类比较困难的预测问题。
与常见的回归预测模型不同,输入变量之间的“序列依赖性”为时间序列问题增加了复杂度。
一种能够专门用来处理序列依赖性的神经网络被称为 递归神经网络(Recurrent Neural Networks、RNN)。因其训练时的出色性能,长短记忆网络(Long Short-Term Memory Network,LSTM)是深度学习中广泛使用的一种递归神经网络(RNN)。
在本篇文章中,将介绍如何在 R 中使用 keras 深度学习包构建 LSTM 神经网络模型实现时间序列预测。
文章的主要内容:
- 如何为基于回归、窗口法和时间步的时间序列预测问题建立对应的 LSTM 网络。
- 对于非常长的序列,如何在构建 LSTM 网络和用 LSTM 网络做预测时保持网络关于序列的状态(记忆)。
问题描述
“航班旅客数据”是一个常用的时间序列数据集,该数据包含了 1949 至 1960 年 12 年间的月度旅客数据,共有 144 个观测值。
下载链接:international-airline-passengers.csv
长短记忆网络
长短记忆网络,或 LSTM 网络,是一种递归神经网络(RNN),通过训练时在“时间上的反向传播”来克服梯度消失问题。
LSTM 网络可以用来构建大规模的递归神经网络来处理机器学习中复杂的序列问题,并取得不错的结果。
除了神经元之外,LSTM 网络在神经网络层级(layers)之间还存在记忆模块。
一个记忆模块具有特殊的构成,使它比传统的神经元更“聪明”,并且可以对序列中的前后部分产生记忆。模块具有不同的“门”(gates)来控制模块的状态和输出。一旦接收并处理一个输入序列,模块中的各个门便使用 S 型的激活单元来控制自身是否被激活,从而改变模块状态并向模块添加信息(记忆)。
一个激活单元有三种门:
- 遗忘门(Forget Gate):决定抛弃哪些信息。
- 输入门(Input Gate):决定输入中的哪些值用来更新记忆状态。
- 输出门(Output Gate):根据输入和记忆状态决定输出的值。
每一个激活单元就像是一个迷你状态机,单元中各个门的权重通过训练获得。
LSTM 网络回归
时间序列预测中最简单的思路之一便是寻找当前和过去数据(\(X_t, X_{t-1}, \dots\))与未来数据($ X_{t+1}$)之间的关系,这种关系通常会表示成为一个回归问题。
下面着手将时间序列预测问题表示成一个回归问题,并建立 LSTM 网络用于预测,用 t-1 月的数据预测 t 月的数据。
首先,加载相关 R 包。
library(keras)
library(dplyr)
library(ggplot2)
library(ggthemes)
library(lubridate)
神经网络模型在训练时存在一定的随机性,所以要为计算统一随机数环境。
set.seed(7)
画出整体数据的曲线图,对问题有一个直观的认识。
dataframe <- read.csv(
'international-airline-passengers.csv')
dataframe$Month <- paste0(dataframe$Month,'-01') %>%
ymd()
ggplot(
data = dataframe,
mapping = aes(
x = Month,
y = passengers)) +
geom_line() +
geom_point() +
theme_economist() +
scale_color_economist()
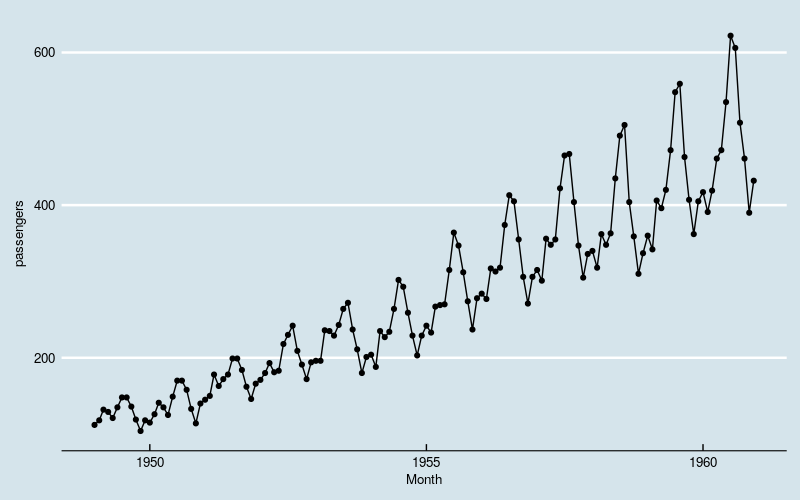
图1
数据体现出“季节性”,同时存在线性增长和波动水平增大的趋势。
将数据集分成两部分:训练集和测试集,比例分别占数据集的 2/3 和 1/3。LSTM 网络对数据的“标度”比较敏感,最好将数据缩放到 0 到 1 之间。
max_value <- max(dataframe$passengers)
min_value <- min(dataframe$passengers)
spread <- max_value - min_value
dataset <- (dataframe$passengers - min_value) / spread
create_dataset <- function(dataset,
look_back = 1)
{
l <- length(dataset)
dataX <- array(dim = c(l - look_back, look_back))
for (i in 1:ncol(dataX))
{
dataX[, i] <- dataset[i:(l - look_back + i - 1)]
}
dataY <- array(
data = dataset[(look_back + 1):l],
dim = c(l - look_back, 1))
return(
list(
dataX = dataX,
dataY = dataY))
}
train_size <- as.integer(length(dataset) * 0.67)
test_size <- length(dataset) - train_size
train <- dataset[1:train_size]
test <- dataset[(train_size + 1):length(dataset)]
cat(length(train), length(test))
96 48
为训练神经网络对数据做预处理,用数据构造出两个矩阵,分别是“历史数据”(作为预测因子)和“未来数据”(作为预测目标)。这里用最近一个月的历史数据做预测。和一般的回归问题相比,LSTM 要求输入数据提供一个额外的维度——时间步。
look_back <- 1
trainXY <- create_dataset(train, look_back)
testXY <- create_dataset(test, look_back)
dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)
# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], 1, dim_train[2])
dim(testXY$dataX) <- c(dim_test[1], 1, dim_test[2])
下面构造神经网络的框架结构并用处理过的训练数据训练。
model <- keras_model_sequential()
model %>%
layer_lstm(
units = 4,
input_shape = c(1, look_back)) %>%
layer_dense(
units = 1) %>%
compile(
loss = 'mean_squared_error',
optimizer = 'adam') %>%
fit(trainXY$dataX,
trainXY$dataY,
epochs = 100,
batch_size = 1,
verbose = 2)
训练结果如下。
trainScore <- model %>%
evaluate(
trainXY$dataX,
trainXY$dataY,
verbose = 2)
testScore <- model %>%
evaluate(
testXY$dataX,
testXY$dataY,
verbose = 2)
sprintf(
'Train Score: %.4f MSE (%.4f RMSE)',
trainScore * spread^2,
sqrt(trainScore) * spread)
sprintf(
'Test Score: %.4f MSE (%.4f RMSE)',
testScore * spread^2,
sqrt(testScore) * spread)
[1] "Train Score: 542.2175 MSE (23.2856 RMSE)"
[1] "Test Score: 2420.2046 MSE (49.1956 RMSE)"
把训练数据的拟合值、测试数据的预测值和原始数据画在一起。
trainPredict <- model %>%
predict(
trainXY$dataX,
verbose = 2)
testPredict <- model %>%
predict(
testXY$dataX,
verbose = 2)
trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value
df <- data.frame(
index = 1:length(dataset),
value = dataset * spread + min_value,
type = 'raw') %>%
rbind(
data.frame(
index = 1:length(trainPredict) + look_back,
value = trainPredict,
type = 'train')) %>%
rbind(
data.frame(
index = 1:length(testPredict) + look_back + length(train),
value = testPredict,
type = 'test'))
ggplot(data = df) +
geom_line(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_point(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_vline(
xintercept = length(train) + 0.5) +
theme_economist() +
scale_color_economist()
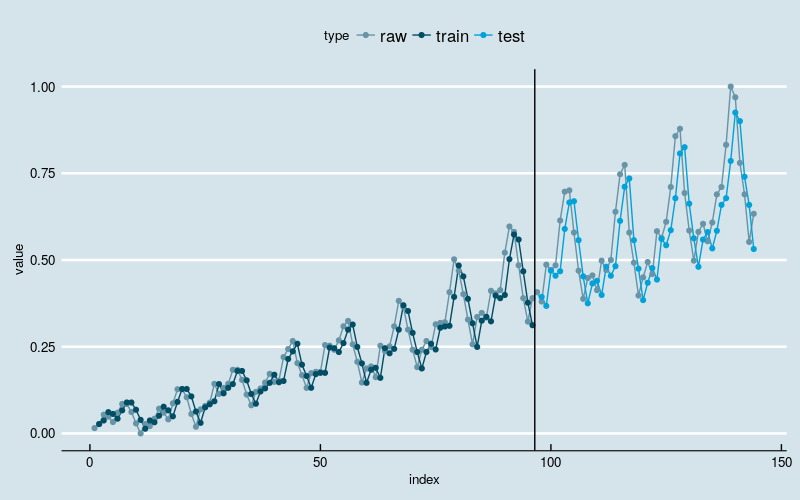
图2
黑线左边是训练部分,右边是测试部分。
结果和多层感知机回归一样。神经网络模型抓住了数据线性增长和波动率逐渐增加的两大趋势,在不做数据转换的前提下,这是经典的时间序列分析模型不容易做到的;但是很可能没有识别出“季节性”的结构特点,因为训练和预测结果和原始数据之间存在“平移错位”。
LSTM 网络回归结合窗口法
前面的例子可以看出,如果仅使用\(X_{t-1}\)来预测\(X_t\),很难让神经网络模型识别出“季节性”的结构特征,因此有必要尝试增加“窗口”宽度,使用更多的历史数据(包含一个完整的周期)训练模型。
下面将数 create_dataset 中的参数 look_back 设置为 12,用来包含过去 1 年的历史数据,重新训练模型。
set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <- create_dataset(test, look_back)
dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)
# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], 1, dim_train[2])
dim(testXY$dataX) <- c(dim_test[1], 1, dim_test[2])
model <- keras_model_sequential()
model %>%
layer_lstm(
units = 4,
input_shape = c(1, look_back)) %>%
layer_dense(
units = 1) %>%
compile(
loss = 'mean_squared_error',
optimizer = 'adam') %>%
fit(trainXY$dataX,
trainXY$dataY,
epochs = 100,
batch_size = 1,
verbose = 2)
trainScore <- model %>%
evaluate(
trainXY$dataX,
trainXY$dataY,
verbose = 2)
testScore <- model %>%
evaluate(
testXY$dataX,
testXY$dataY,
verbose = 2)
sprintf(
'Train Score: %.4f MSE (%.4f RMSE)',
trainScore * spread^2,
sqrt(trainScore) * spread)
sprintf(
'Test Score: %.4f MSE (%.4f RMSE)',
testScore * spread^2,
sqrt(testScore) * spread)
trainPredict <- model %>%
predict(
trainXY$dataX,
verbose = 2)
testPredict <- model %>%
predict(
testXY$dataX,
verbose = 2)
trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value
df <- data.frame(
index = 1:length(dataset),
value = dataset * spread + min_value,
type = 'raw') %>%
rbind(
data.frame(
index = 1:length(trainPredict) + look_back,
value = trainPredict,
type = 'train')) %>%
rbind(
data.frame(
index = 1:length(testPredict) + look_back + length(train),
value = testPredict,
type = 'test'))
ggplot(data = df) +
geom_line(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_point(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_vline(
xintercept = length(train) + 0.5) +
theme_economist() +
scale_color_economist()
[1] "Train Score: 182.7605 MSE (13.5189 RMSE)"
[1] "Test Score: 1518.8280 MSE (38.9721 RMSE)"
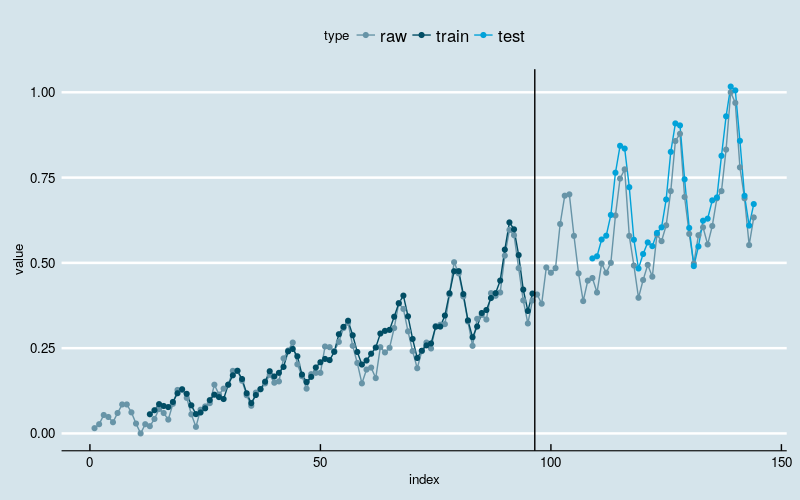
图3
结果和多层感知机回归一样。新的模型基本上克服了“平移错位”的现象,同时依然能够识别出线性增长和波动率逐渐增加的两大趋势。
基于时间步的 LSTM 网络回归
和一般的回归问题不同,LSTM 网络的数据输入包括而外的维度——时间步(time steps)。
一些序列问题的样本可能有不同数量的时间步。例如,测量现实中一台机器的故障点或喘振点。每个事件将是一个样本,触发事件的观测正是时间步,而观察到的变量就是特征。
时间步提供了另一种方式来解释我们的时间序列问题,就像在窗口法例子那样,可以将时间序列中之前的时间步作为输入来预测下一个时间步的输出。
set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <- create_dataset(test, look_back)
dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)
# reshape input to be [samples, time steps, features]
dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)
model <- keras_model_sequential()
model %>%
layer_lstm(
units = 4,
input_shape = c(look_back, 1)) %>%
layer_dense(
units = 1) %>%
compile(
loss = 'mean_squared_error',
optimizer = 'adam') %>%
fit(
trainXY$dataX,
trainXY$dataY,
epochs = 100,
batch_size = 1,
verbose = 2)
trainScore <- model %>%
evaluate(
trainXY$dataX,
trainXY$dataY,
verbose = 2)
testScore <- model %>%
evaluate(
testXY$dataX,
testXY$dataY,
verbose = 2)
sprintf(
'Train Score: %.4f MSE (%.4f RMSE)',
trainScore * spread^2,
sqrt(trainScore) * spread)
sprintf(
'Test Score: %.4f MSE (%.4f RMSE)',
testScore * spread^2,
sqrt(testScore) * spread)
trainPredict <- model %>%
predict(
trainXY$dataX,
verbose = 2)
testPredict <- model %>%
predict(
testXY$dataX,
verbose = 2)
trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value
df <- data.frame(
index = 1:length(dataset),
value = dataset * spread + min_value,
type = 'raw') %>%
rbind(
data.frame(
index = 1:length(trainPredict) + look_back,
value = trainPredict,
type = 'train')) %>%
rbind(
data.frame(
index = 1:length(testPredict) + look_back + length(train),
value = testPredict,
type = 'test'))
ggplot(data = df) +
geom_line(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_point(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_vline(
xintercept = length(train) + 0.5) +
theme_economist() +
scale_color_economist()
[1] "Train Score: 370.2546 MSE (19.2420 RMSE)"
[1] "Test Score: 6277.8128 MSE (79.2326 RMSE)"
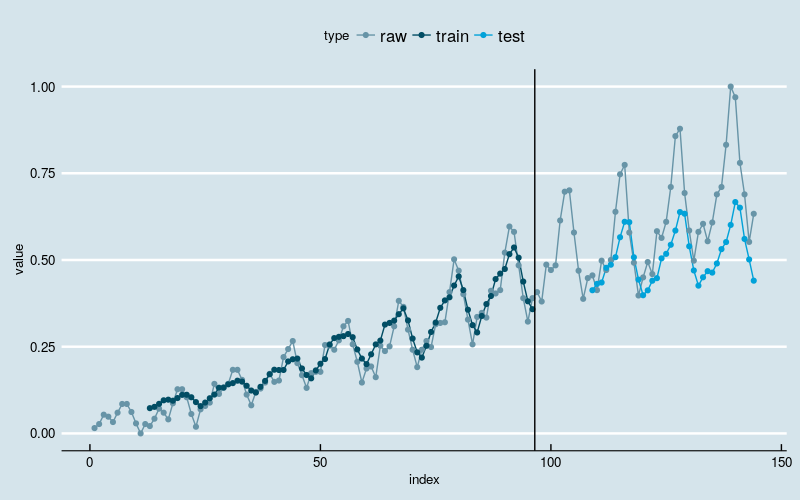
图4
很不幸,结果变差了。训练部分的拟合结果看起来像某种平滑,特别是在最开始的部分。训练数据的前半部分波动较小,后半部分波动大,拟合的结果反映出神经网络发现了这一点,拟合曲线的波动迅速放大。测试部分的预测结果通常是在低估实际值,说明网络并未“记住”波动放大的趋势。
在批量训练之间保持 LSTM 的记忆
LSTM 网络拥有记忆,可以记住长序列中的某些规律或特征。
通常,网络的状态在训练过程中会被重置,在调用model.predict() 或 model.evaluate() 时也会。
在 keras 中只要声明 LSTM 网络是“有状态的”就可以轻易控制 LSTM 网络中的内部状态。这意味着可以在训练和预测过程中保持状态的稳定。
保持状态稳定要求训练数据不能被打乱,同时要在训练一次之后手动的重置网络状态。也就是说,每一次循环都要训练一次并重置一次网络状态。
for (i in 1:100)
{
model %>%
fit(trainXY$dataX,
trainXY$dataY,
epochs = 1,
batch_size = batch_size,
verbose = 2,
shuffle = FALSE)
model %>%
reset_states()
}
最后,LSTM 网络的参数 stateful 必须设置为 TRUE,不同于设定输入的维度,必须对样本个数、时间步个数和时间步的特征个数硬编码。
model %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size, # batch_size
look_back, # time_steps
1), # features
stateful = TRUE)
预测也就变成了
model %>%
predict(
trainXY$dataX,
batch_size = batch_size)
完整代码
set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <- create_dataset(test, look_back)
dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)
dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)
batch_size = 1
model <- keras_model_sequential()
model %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size,
look_back,
1),
stateful = TRUE) %>%
layer_dense(
units = 1) %>%
compile(
loss = 'mean_squared_error',
optimizer = 'adam')
for (i in 1:100)
{
model %>%
fit(
trainXY$dataX,
trainXY$dataY,
epochs = 1,
batch_size = batch_size,
verbose = 2,
shuffle = FALSE)
model %>%
reset_states()
}
trainPredict <- model %>%
predict(
trainXY$dataX,
batch_size = batch_size,
verbose = 2)
model %>%
reset_states()
testPredict <- model %>%
predict(
testXY$dataX,
batch_size = batch_size,
verbose = 2)
trainScore <- var(trainXY$dataY - trainPredict) * spread^2
testScore <- var(testXY$dataY - testPredict) * spread^2
sprintf(
'Train Score: %.4f MSE (%.4f RMSE)',
trainScore,
sqrt(trainScore))
sprintf(
'Test Score: %.4f MSE (%.4f RMSE)',
testScore,
sqrt(testScore))
trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value
df <- data.frame(
index = 1:length(dataset),
value = dataset * spread + min_value,
type = 'raw') %>%
rbind(
data.frame(
index = 1:length(trainPredict) + look_back,
value = trainPredict,
type = 'train')) %>%
rbind(
data.frame(
index = 1:length(testPredict) + look_back + length(train),
value = testPredict,
type = 'test'))
ggplot(data = df) +
geom_line(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_point(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_vline(
xintercept = length(train) + 0.5) +
theme_economist() +
scale_color_economist()
[1] "Train Score: 338.1505 MSE (18.3889 RMSE)"
[1] "Test Score: 2299.0873 MSE (47.9488 RMSE)"
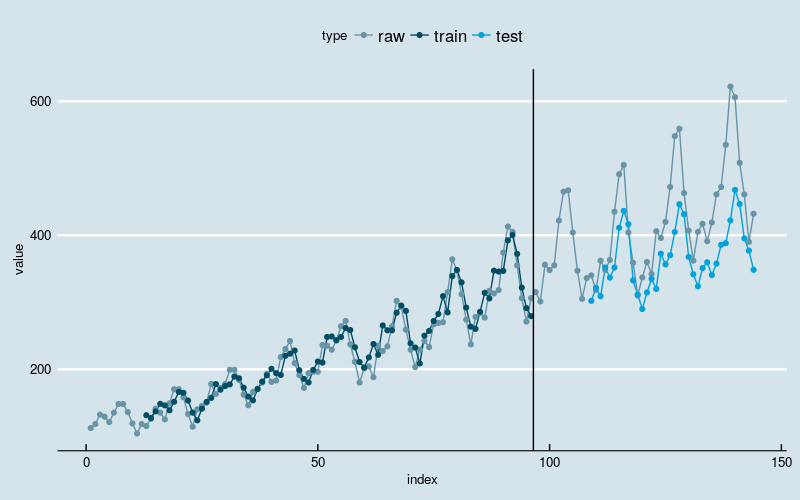
图5
和上面的例子相比,没有明显改善。
在批量训练中堆叠 LSTM 网络
最后,介绍一下 LSTM 网络的一大优点:可以通过堆叠构建更深度的神经网络架构。
keras 中 LSTM 网络可以方便的实现堆叠。需要注意的是中间层级的 LSTM 网络的输出形式必须是序列,只要将参数 return_sequences 设置为 TRUE 就可以了。
扩展前面用到的 LSTM 网络,堆叠两个层级。
model %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size,
look_back,
1),
stateful = TRUE,
return_sequences = TRUE) %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size,
look_back,
1),
stateful = TRUE)
完整的代码
set.seed(7)
look_back <- 12
trainXY <- create_dataset(train, look_back)
testXY <- create_dataset(test, look_back)
dim_train <- dim(trainXY$dataX)
dim_test <- dim(testXY$dataX)
dim(trainXY$dataX) <- c(dim_train[1], dim_train[2], 1)
dim(testXY$dataX) <- c(dim_test[1], dim_test[2], 1)
batch_size = 1
model <- keras_model_sequential()
model %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size,
look_back,
1),
stateful = TRUE,
return_sequences = TRUE) %>%
layer_lstm(
units = 4,
batch_input_shape = c(
batch_size,
look_back,
1),
stateful = TRUE) %>%
layer_dense(
units = 1) %>%
compile(
loss = 'mean_squared_error',
optimizer = 'adam')
for (i in 1:100)
{
model %>%
fit(trainXY$dataX,
trainXY$dataY,
epochs = 1,
batch_size = batch_size,
verbose = 2,
shuffle = FALSE)
model %>%
reset_states()
}
trainPredict <- model %>%
predict(
trainXY$dataX,
batch_size = batch_size,
verbose = 2)
model %>%
reset_states()
testPredict <- model %>%
predict(
testXY$dataX,
batch_size = batch_size,
verbose = 2)
trainScore <- var(trainXY$dataY - trainPredict) * spread^2
testScore <- var(testXY$dataY - testPredict) * spread^2
sprintf(
'Train Score: %.4f MSE (%.4f RMSE)',
trainScore,
sqrt(trainScore))
sprintf(
'Test Score: %.4f MSE (%.4f RMSE)',
testScore,
sqrt(testScore))
trainPredict <- trainPredict * spread + min_value
testPredict <- testPredict * spread + min_value
df <- data.frame(
index = 1:length(dataset),
value = dataset * spread + min_value,
type = 'raw') %>%
rbind(
data.frame(
index = 1:length(trainPredict) + look_back,
value = trainPredict,
type = 'train')) %>%
rbind(
data.frame(
index = 1:length(testPredict) + look_back + length(train),
value = testPredict,
type = 'test'))
ggplot(data = df) +
geom_line(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_point(
mapping = aes(
x = index,
y = value,
color = type)) +
geom_vline(
xintercept = length(train) + 0.5) +
theme_economist() +
scale_color_economist()
[1] "Train Score: 1150.3215 MSE (33.9164 RMSE)"
[1] "Test Score: 5795.0083 MSE (76.1250 RMSE)"
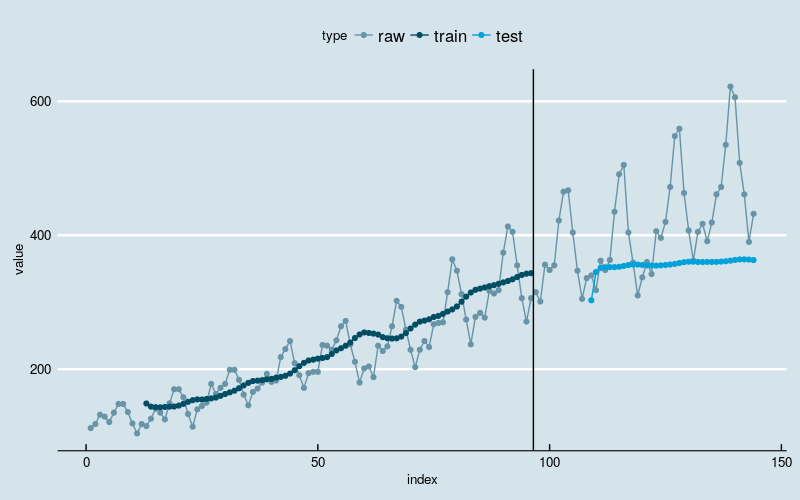
图6
几乎是最差的结果。训练部分网络仅仅能够识别出了数据的大体增长趋势,但在测试部分,网络看起来把学习到的东西全“忘记”了。
总结
尺有所短,寸有所长。
尽管更加复杂先进 LSTM 网络在其他领域取得了出色的表现,但在这个具体的例子上,表现却不如更简单的多层感知机回归。反思问题的原因:
- 简单模型在“小样本 + 简单模式”的数据集上更容易获得稳健的结果;
- 目前使用的 LSTM 网络结构可能不适应当前的问题。
- 解决问题的方法论——回归,可能对当前的问题是不合适的。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号