6.12（1）线性规划应用案例的求解

（1）线性规划应用案例的求解

1、基本要求

通过一个农业生产计划优化安排的实例求解，培养学生解决实际线性规划问题的初步能力；熟悉线性规划的建模过程；掌握Matlab优化工具箱中线性规划函数的调用。

2、主要内容

某村计划在100公顷的土地上种植a、b、c三种农作物。可以提供的劳力、粪肥和化肥等资源的数量，种植每公顷农作物所需这三种资源的数量，以及能够获得的利润如表所示。

种植投入产出表

	用  工	粪肥（吨）	化肥（千克）	利润（元）
a	450	35	350	1500
b	600	25	400	1200
c	900	30	300	1800
可提供资源	63000	3300	33000

其中一个劳动力干一天为1个工。现在要求为该村制定一个农作物的种植计划，确定每种农作物的种植面积，使得总利润最大。

3、操作要点

（1）建立线性规划的数学模型；

（2）安装Matlab优化工具箱（Optimization Toolbox），并学习工具箱中求解线性规划的函数；

（3）利用Matlab优化工具箱解线性规划问题。

（4）运行该程序，在命令窗记录下最优解x和对应的最优值fval。

（5）按照模板撰写实验报告，要求规范整洁。

4、主要仪器设备

微机及Matlab软件

 

f=[1500 1200 1800];

 f=-f;

a=[450 600 900;35 25 30;350 400 300];

 b=[63000 3300 33000];

acq=[1 1 1];

 aeq=[1 1 1];

 beq=[100];

 lb=zeros(3,1);

 [zui,zong,exitflag,output,lamdba]=linprog(f,a,b,aeq,beq,lb)

 

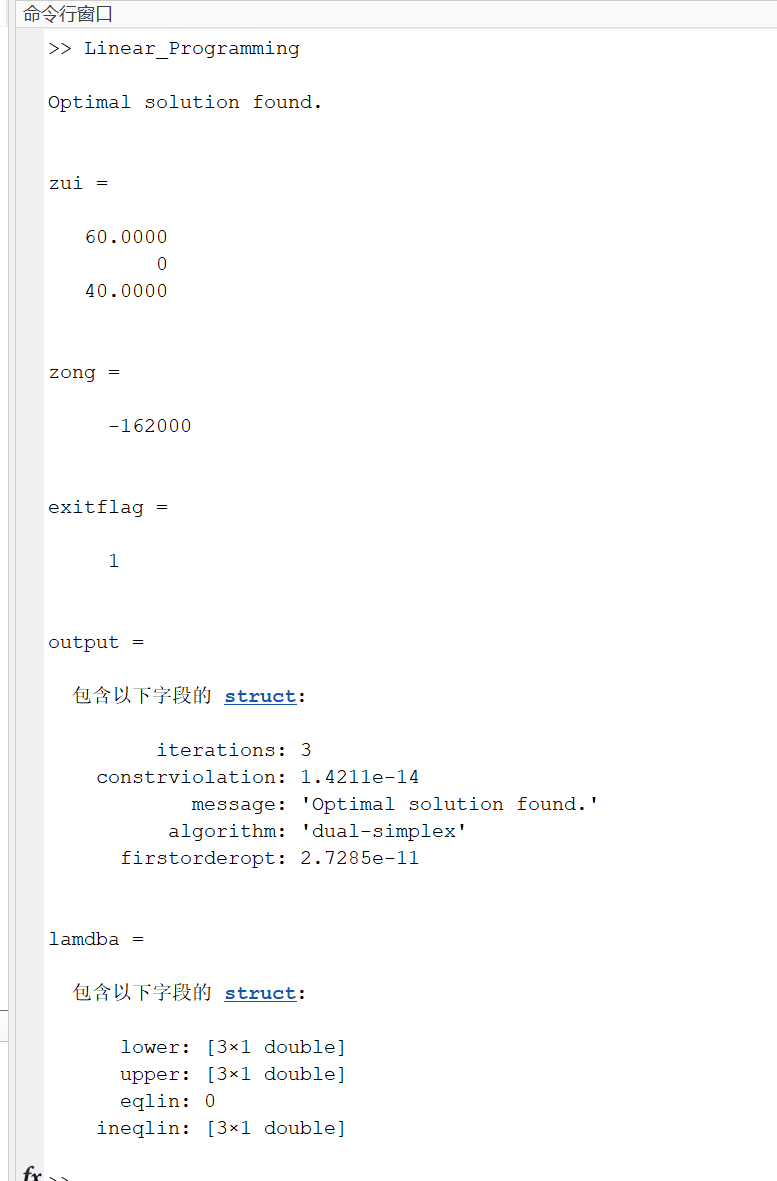
最优种植方案为种植A作物60公顷，B作物0公顷，C作物40公顷，总利润16200元。