为什么74汉明码只能检测2bit以内的错误
74汉明码是奇偶校验的加强版,属于块校验。即假设信息位有n位,校验位k位,假设只有1bit错误的前提下,n+k位就有n+k种1bit错误情况,加上没有出错的情况,总共n+k+1种情况,k位校验要覆盖以上所有的n+k+1,则有
2^k >= n+k+1
假设n = 4 ,则根据上式,得出k=3 其实就是7,4汉明码
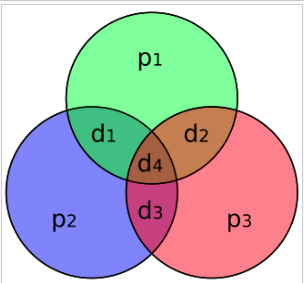
上图,p1 p2 p3 为校验位,d1 d2 d3 d4 为信息位
假设有1bit错误,假设p2校验结果正确,p1和p3不正确,就是说d1 d3 d4都正确,从图中也能看出是d2出错了
注意上述分析都是建立在明确只有1bit错误的情况下,假设2bit错误,还是上述条件,则因为奇偶校验的不能识别偶数个bit出错这个局限性
有可能是d1和d3两个都出错,这样p2还是正确,然后p1和p3不正确,也就是说7,4汉明码没法区分1bit还是2bit出错这两种情况
如何判断是2bit错误?发生了错误后,校验子非0,我们知道校验子的值指向错误的bit位,当发生错误时,没办法判断是1bit还是多bit,

汉明码最小距离是3,解释下汉明距离:
就是任意两个数据的编码,最小有几位不同,比如最小距离是1的编码方式:
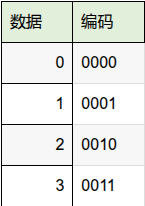
n位编码,表示2^n个数,这种抗干扰的效果最差,因为两个合法码字之间最小汉明间距为1,意味着发生任何一个码字只要有1bit变化都可以变成另外一个合法的码字,接收端就不可能判断出哪里出错。比如数据0发生了1bit错误,可能是4'b0001 4'b0010 4'b0100 4'b1000,这4个值都有对应的合法编码的数。
再看最小汉明距离为2的情况:
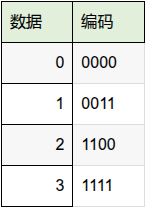
这种情况下,假设还是数据0发生了1bit错误,变成了4'b0001,则错误的情况都找不到合法对应的码字,所以接收端可以判断出错了,但是具体是哪一个bit出错就不知道了,因为4'b0011也可能发生1bit错误变成4'b0001,和前面的错误是一样的,没法判断。所以可以检测1bit错误,没法纠错
最小汉明距离为3的情况:
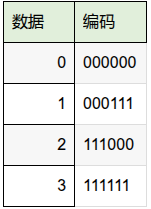
在最小距离为3时,任意两个有效码字之间有3位不同,当发生了1bit错误时,错误的编码距离原本正确的编码距离为1,就是只有1位不同,而距离任意其他合法的码字距离都大于等于2,接收端就能知道哪个bit错了并且纠正出来,比如数据0错了,6'b000001,6'b000010,6'b000100,6'b001000,6'b010000,6'b100000,这6种可能的错误情况都没有相应的编码,接收端就知道错了,这几个错误的情况和数据0的编码只有1个距离,所以是数据0错了。
但是如果发生了2bit错误,比如变成了6'b000011,就会和数据1的编码6'b000111只相差1位,接收端会认为是数据1错误了,从而纠正成数据1,但是实际是数据0错了,也就是说它没法区分是1bit还是2bit错误,而7,4汉明码就是这种情况,在这种情况下,即使纠正了,校验还是会失败,下图所示,7,4汉明码最小距离为3,4+3位共128种情况下,只有这16种编码是正确的,其他都是错误的
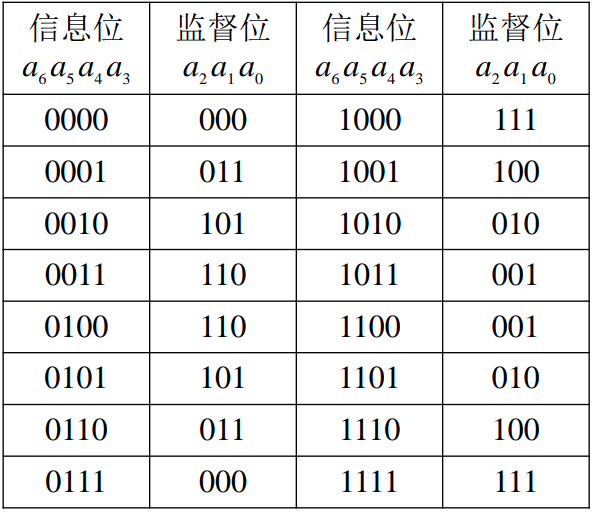
所以我们说7,4汉明码可以1bit检错和纠错,2bit检错,指的是它在发生2bit错误情况下,也能检测出错误,就是说校验子是非0的。但是它不能区分是1bit还是2bit错误。假设按照1bit去纠正,纠正的就还是错误的。
汉明码的最小距离为3,这意味着解码器可以检测和纠正单个错误,但无法区分某个代码字的双比特错误与不同代码字的单个比特错误。因此,除非没有尝试校正,否则某些双位错误将被错误地解码,就好像它们是单位错误一样,因此无法被检测到
当发生双比特错误时,(7,4)汉明码会将该事件解释为需要纠正的"伪单比特错误"。
若在汉明码基础上额外增加一个全局奇偶校验位(P),由此形成的扩展汉明码(8,4)的码字间最小距离将提升至(d=4)。
如果发生3bit错误??,有可能接受端就会检测不出来错误,因为这已经达到最小汉明距离了,就是错的可能正好是一个对的数的编码。这种就不考虑了,因为同时发生3bit错误概率很低,换句话说,选择74汉明码就是在已知当前系统几乎只会发生1bit的错误,其他错误默认不会发生。
参:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号