CRC的错检率
CRC校验很常见,我们也经常用,比如以太网MAC帧的结尾4个字节的FCS就是CRC32的校验结果,以前我以为加个CRC,或者有校验,就能保证这个数据有错误接收方一定能判断出来,后面自己写这些校验代码时候,就发现原来不是这么回事,就是说两个不同的数据,CRC对其校验,结果可能是一致的,也就是说可能数据在传输的过程中发生了bit翻转,但是接收方校验计算出的结果还和发送方发过来的一样,就是校验通过了,这个情况有个专业术语叫CRC碰撞,算法上有点类似生日悖论,它的叙述是:“需要多少人聚在一起,才能让其中至少有两人同一天生日的概率超过一半?”
答案是只需要23人。这个问题有时被称为“生日悖论”,不过这其实并不是真正的悖论,只是因为结果违反了一般人的直觉。大多数人会认为23人中两人同生日的概率应该远小于50%。它派生出的数学理论被用于设计一种名为“生日攻击”的密码破解方法。具体是这样算的:
1 - 1*(364/365)*(363/365)*(362/365)....
就是1减去生日各不相同的概率,第一个人生日概率不相同概率为1,第二个人和第一个不同一天出生,概率就是364/365,第三个和前两个不同一天的概率为363/365,一直下去...
这个结果表如下:
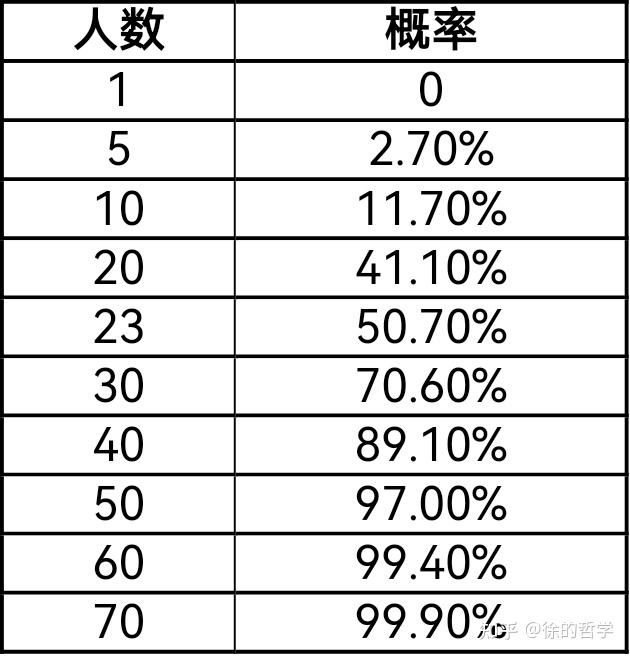
所以只需要有23个人同时在场,有两人同一天生日的概率就会超过50%。
CRC碰撞同理,以CRC32为例,理论上来说它有2的32次方的数据可能,也就说对应2的32次方的数据样本,可以对应这2的32次方的CRC32值,很多人就认为它的重复率,也就是碰撞率是1/2^32,其实是不对的,这个是单对消息的重复概率,换句话说,是任意两条数据它们的CRC32一致的概率是这么多,你可以理解为已经有一个数据的CRC32的值了(独立事件,可以理解为有放回),然后再挑一个数据,使得和上一个数据的CRC32值一样,这个的概率是1/2^32。但是CRC碰撞的概率不是指定这一对,而是很多对,A和B相同的概率是一个,C和D概率相同的又是一个,就是说在指定样本中,有多少种两两组合的方式,然后乘以单对的概率,就是总体的碰撞概率。举个例子,有2的32次方的不同颜色小球,指定两次都是黄色的概率是1/2^32,但是还有两次都是其他颜色的情况,这种也算碰撞,不是非要黄色才是,用公式表达:
- 两两组合种类:
- N(N−1)/2,其实就是概率论里的C几几的那个公式,
- 单对重复概率:
- 1/2^32
现在我们可以计算下,网上有个CRC碰撞的实验测试数据,我们先来看下:
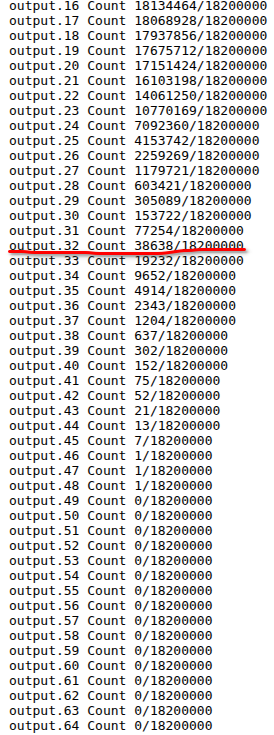
图里CRC32在1820w条样本数据情况下,出现了38638个重复值,用公式验证下:
- 18200000*18199998/2*1/2^32 = 38561.406964436
可以看到在样本数最够大并且是随机情况下,实际值和理论值是非常接近的,如果进一步扩大样本量,就会更靠近理论值。
参:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号