2023 省选做题记录 4.0
不要那么摆了!!!!
2.21
[UOJ763] 树哈希(树哈希)
学到了 zqy 的一种神奇方法。类似 https://peehs-moorhsum.blog.uoj.ac/blog/7891。
实际上就是随机一个映射。
更大的好处是它支持换根!!!!!
代码:https://paste.ubuntu.com/p/pD9q2MRqH3/。
2023.2.20 考试 T2 树(tree)(树哈希 + 暴力)
题意:
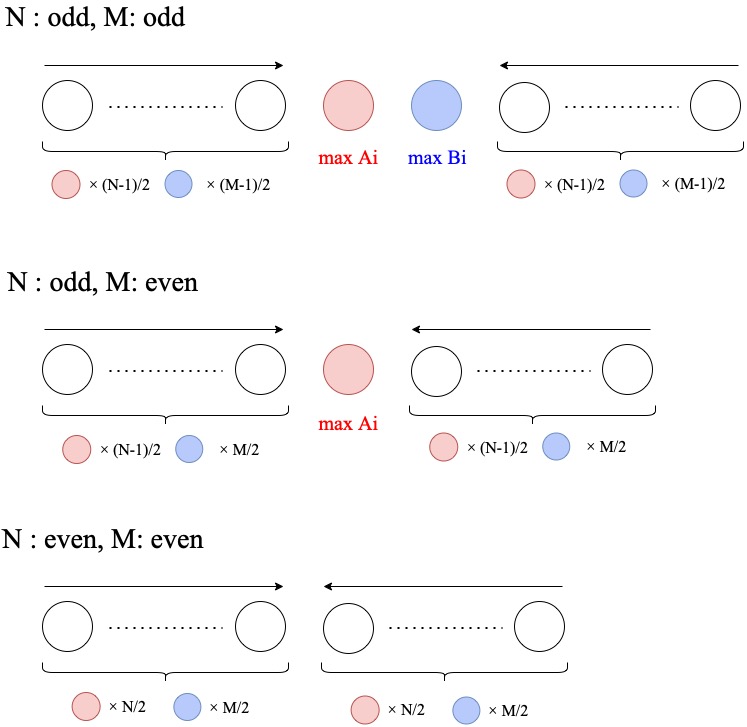
定义有根树的乘法如下:\(T=A\times B\) 表示对于 \(A\) 的每一个节点复制一个 \(B\) 然后将这个节点与 \(B\) 的根合并起来。
具体见下图:
我们称 \(A,B\) 为 \(T\) 的因子。显然的,\(T\times 1=1\times T=T\),其中 \(1\) 是只有一个节点的有根树。所以 \(1\) 是 \(T\) 的因子,\(T\) 也是自己的因子。如果一个有根树的因子只有 \(1\) 和 \(T\),那么我们称 \(T\) 是 质树(\(1\) 不是质树)。
给定一个由 \(1\) 标号到 \(n\) 的有根树(根为 \(1\)),你希望将这个树分解为尽量多的质树(也就是使得 \(T=T_1\times T_2\times T_3\times\cdots\times T_m\),\(T_i\) 都是质树且 \(m\) 尽量大)。求出最大的质树数量。
多组数据。
数据范围:\(\sum n\le 10^6\)。
从大到小枚举所有可能的因子,并且依次尝试拆分整棵树。实际上就是从叶子开始向上贪心,每次找到指定 \(size\) 的子树并将其割掉,判断这些割掉的子树是否同构。
因为每个点父亲的编号比它小,所以可以直接倒序循环一遍做这个过程。
树哈希可以套用上一题的方法。
代码:https://paste.ubuntu.com/p/D7h8BBpPM7/。
2023.2.20 考试 T1 疏(sparse)(结论)
题意:
在无限大的棋盘上有一个马。马可以执行一些移动操作。移动操作由两个数定义:第一个数表示移动了
多少行(正数代表向下,负数代表向上,\(0\) 代表不变),第二个数表示移动了多少列(正数代表向右,负
数代表向左,\(0\) 代表不变)。你希望马可以到达无限大的棋盘上的任意一个位置。给定一些移动操作,询
问是否可以通过这些移动操作到达任意位置。数据范围:数据组数 \(1\le T\le 10000\),\(1\le n\le 100\),\(-100\le p,q\le 100\)。
结论题,见代码,不会证。
代码:https://paste.ubuntu.com/p/pdR3Hxnjpv/。
2023.2.20 考试 T3 数(count)(DP + 推式子)
题意:
有 \(n\) 道题目,第 \(i\) 道题目初始分数为 \(a_i\)。有 \(m\) 个裁判为题目评分,每个裁判会 恰好 选择 \(v\) 个题目使得它们的分数 \(+1\)。
评分完毕后,你会将所有的题目按照分数从高往低排序,如果两个题目分数相同你可以任意决定它们的顺序。接下来你会选择一个数 \(p\)(\(1\le p\le n\)),排序后的前 \(p\) 个题目会被选入比赛中。
请求出有多少种不同的比赛,对 \(998244353\) 取模。两个比赛被认为是不同的当且仅当有一个题目在一个比赛中却不在另一个中。
数据范围:\(m,a_i,\sum n\le 100\)。
设 \(S\) 表示最后被选中的题目集合(\(|S|=p\)),\(T\) 表示最后没被选中的题目集合。
按照 \(p\le v\) 和 \(p>v\) 考虑:
-
当 \(p\le v\) 时,策略肯定是每次必选这 \(p\) 道题目,然后在剩下的题目中选 \(v-p\) 道分数最低的。所以第 \(p\) 大的分数就是 \(\min\limits_{x\in S}a_x+m\),显然这个值要不小于 \(T\) 中的最大值。\(S\) 和 \(T\) 合法的条件就是:
\[\sum\limits_{x\in T,a_x\ge \min S}\min S+m-a_x\ge m(v-p)\\ \sum\limits_{x\in T,a_x\ge \min S}a_x-m-\min S\le m(p-v)\\ \sum\limits_{x\in T,a_x\ge \min S}a_x-\min S\le m(n-v) \]可以枚举 \(S\) 中最小值的位置,然后对这个不等式进行 DP。具体的,设 \(f_{i,j}\) 表示考虑到第 \(i\) 个,不等式左边的值为 \(j\) 的方案数。
-
当 \(p>v\) 时,策略肯定是每次选择 \(S\) 中分数最低的 \(v\) 个,所以第 \(p\) 大肯定不小于 \(\max\limits_{x\in T}a_x\)。合法条件显然是 \(\sum\limits_{x\in S,\max T-m\le a_x\le \max T}\max T-a_x\le mv\),同样做一遍上面的 DP 即可。
-
但这样可能会多算不属于某种情况的方案,直接用一个组合数减掉就可以了。
代码:https://paste.ubuntu.com/p/8y5Xc396cD/。
2023.2.21 考试 T1 铝(al)(DP + 概率)
题意:
小 Y 在玩他喜欢的游戏。在这个游戏中他需要通过 \(n\) 关。
初始时他在关卡 1,在关卡 \(i\) 时他可以花费 \(1\) 单位的时间挑战这个关卡,有 \(p_i\) 的概率挑战成功到第 \(i+1\) 关;否则他会挑战失败,受到一点伤害且停在第 \(i\) 关。
玩家有两个属性:体力值 \(hp\) 和灵魂 \(mp\)。任意时刻,玩家可以执行以下三种操作之一:
- 花费 \(1\) 单位时间挑战当前关卡 \(i\),有 \(p_i\) 的概率到第 \(i+1\) 关(若 \(i=n\) 则挑战成功),有 \(1−p_i\) 的概率留在第 \(i\) 关并受到一点伤害,即体力值减一。
- 聚集,当 \(mp\) 非零时用 \(T_1\) 单位时间消耗一点 \(mp\) 恢复一点 \(hp\)。
- 使用蜂巢之血,用 \(T_2\) 单位时间恢复一点 \(hp\),但此操作只能在受到一点伤害后立即使用一次。
因为小 Y 不想让他的体力值在任何一个时刻变成 \(0\),因此只能在 \(hp\) 大于 \(1\) 时进行一操作。
有些关卡有灵魂图腾,当玩家处于有灵魂图腾的关卡时,他可以无限次使用灵魂图腾,使 \(mp\) 恢复到上限。
小 Y 的体力值上限为 \(H\),灵魂上限为 \(S\),初始时他的体力值和灵魂均达到上限,即 \(hp = H, mp = S\)。
现在小 Y 找到了你,希望你能帮他设计一种策略使得期望下他挑战成功的时间最短。
数据范围:\(1 ≤ n ≤ 1000, 2 ≤ H ≤ 9, 0 ≤ S ≤ 6, 1 ≤ P_i ≤ 99, 0 ≤ K ≤ n, 1 ≤ a_i ≤ n, a_i <a_{i+1} , 1 ≤ T_1 , T_2 ≤ 100\)。
这种有关策略的期望题,要考虑到一个很重要的套路:倒着做。
设 \(f_{i,j,k}\) 表示倒着扫已经扫到了 \(i\),现在 \(hp=j,mp=k\) 的期望最短时间。
先不考虑灵魂图腾的情况,那么一个状态可以直接挑战成功,或者在挑战失败之后用聚集,或者直接用若干次聚集,或者使用蜂巢之血。
- 对于前两种转移,有 \(f_{i,j,k}=1+p_i\times f_{i+1,j,k}+(1-p_i)\times\min(f_{i,j-1,k},f_{i,j,k-1}+T_1)\)。
- 对于第三种转移,直接枚举使用次数即可。
- 对于第四种转移,有 \(f_{i,j,k}=1+p_i\times f_{i+1,j,k}+(1-p_i)\times(f_{i,j,k}+T_2)\),移项可得 \(f_{i,j,k}=\frac{1+p_i\times f_{i+1,j,k}+(1-p_i)\times T_2}{p_i}\)。
现在考虑灵魂图腾,用灵魂图腾把灵魂回满对应到 dp 的转移是 \(f_{i,j,s}\to f_{i,j,k}\),因为在一个关卡中最多只需要使用 \(h\) 次灵魂图腾,所以把这一过程做 \(h\) 次即可。
最后特判 \(S=0\) 的情况。
代码:https://paste.ubuntu.com/p/nT9Twx9MS5/。
2.22
222222222222222222222222222222222222222222222222222222222222222222222222222222222222
[BJOI2018] 治疗之雨(高斯消元 + 期望 DP)
首先可以求出在 \(k\) 次减一操作中受到 \(i\) 点伤害的概率 \(P_i=\frac{\binom{k}{i}m^{k-i}}{(m+1)^k}\)。
然后设 \(f_i\) 表示当前血量为 \(i\),期望多少轮操作以后血量会变成 \(0\)。
转移可以考虑一轮操作之后血量由 \(i\) 变成 \(j\) 的概率,即 \(f_i=\sum\limits_{j=1}^i (\frac{m}{m+1}P_{i-j}+\frac{1}{m+1}P_{i-j+1})f_j+\frac{1}{m+1}P_0f_{i+1}+1\)。前面的系数是讨论了加一操作是否作用在当前数上。
直接高斯消元是 \(\mathcal{O}(n^3)\) 的。
注意到这个系数矩阵很有规律,它形如:
1 1 0 0 0 0 ... 0 0 a[1]
1 1 1 0 0 0 ... 0 0 a[2]
1 1 1 1 0 0 ... 0 0 a[3]
...
1 1 1 1 1 1 ... 1 1 a[n-1]
1 1 1 1 1 1 ... 1 1 a[n]
从上往下每次消去第一列,最后得到的矩阵形如:
1 1 0 0 0 0 ... 0 0 a'[1]
0 1 1 0 0 0 ... 0 0 a'[2]
0 0 1 1 0 0 ... 0 0 a'[3]
0 0 0 1 1 0 ... 0 0 a'[4]
0 0 0 0 1 1 ... 0 0 a'[5]
...
0 0 0 0 0 0 ... 1 1 a'[n-1]
0 0 0 0 0 0 ... 0 1 a'[n]
从下往上依次带入即可解出方程。
时间复杂度 \(\mathcal{O}(n^2)\)。
注意多测要清空!!!!
启发:直接高斯消元复杂度太大的时候考虑观察系数矩阵的特殊形态手动消元。
代码:https://paste.ubuntu.com/p/9DQYP8f73C/。
[QOJ5526] The 1st Universal Cup. Stage 4: Ukraine. Problem J. Jewel of Data Structure Problems(结论)
题意:
定义一个序列的奇偶性为其逆序对数量的奇偶性。
给定一个长度为 \(n\) 的排列和 \(Q\) 次操作,每次操作形如交换排列中的两个数。在每次操作之后选择一个子序列使得这个子序列的逆序对个数为奇数,问能选择的最长子序列的长度是多少。如果不能选择任何子序列输出
-1。数据范围:\(1\le n,Q\le 2\times 10^5\)。
显然如果排列为 \((1,2,\dots,n)\),那么答案显然为 \(-1\)。
如果原排列是奇排列,那么答案为 \(n\)。
否则令 \(c_i\) 表示和 \(i\) 相关的逆序对数量(即 \(i\) 前比 \(p_i\) 大的数字个数加上 \(i\) 后比 \(p_i\) 小的数字个数)。如果存在一个 \(c_i\) 是奇数,那么答案为 \(n-1\)(删掉 \(c_i\) 为奇数的那个位置);否则答案为 \(n-2\)(选择一个逆序对并将它们两个数删去)。
接下来考虑怎么求出一个排列的奇偶性。
结论:排列的奇偶性和 \(n-\) 环的个数 的奇偶性相同。每次交换两个位置之后排列的奇偶性都会变化。
后者证明可见 https://blog.csdn.net/choimroc/article/details/103134547。对于前者,考虑一次交换操作可以增加一个环,那么 \(n-\) 环的个数 就是最少的操作次数使得排列变成 \((1,2,\dots,n)\),所以其奇偶性等于排列的奇偶性。
而对于 \(c_i\),假设 \(i\) 之前有 \(x\) 个数比 \(p_i\) 小,那么 \(c_i=(i-1-x)+(p_i-1-x)=i+p_i-2(x+1)\),所以只需要判断 \(i\) 和 \(p_i\) 的奇偶性是否相同。
代码:https://paste.ubuntu.com/p/R27MWNtRy5/。
2023.2.21 考试 T3 磷(p)(性质 + 分类讨论 + 推式子)
题意:
给定一张无向图 \(G\),求 \(L^k(G)\)(即对 \(G\) 求 \(k\) 次线图)的最大独立集大小对 \(998244353\) 取模的结果。
数据范围:\(2\le n,m\le 2000,2\le k\le 7\) 且图没有重边、自环。

代码(\(2\le k\le 5\)):https://paste.ubuntu.com/p/qjk6mrhp47/。
std:https://paste.ubuntu.com/p/hXTSrF6Zsq/。
[QOJ5518] The 1st Universal Cup. Stage 4: Ukraine. Problem B. Binary Arrays and Sliding Sums(组合计数)
题意:
对于一个长度为 \(n\) 的
01序列 \(a_1,a_2,\dots, a_n\),定义一个长度为 \(n\) 的序列 \(f(a)\):
- \(f(a)_i=a_i+a_{i+1}+\dots+a_{i+k-1}\)(假设 \(a_{n+i}=a_i\),即将序列看作一个环)。
问所有不同的 \(f(a)\) 的数量。对 \(998244353\) 取模。
多组数据。
数据范围:\(1\le T\le 10^5,2\le k<n\le 10^6\)。
假设 \(f(a)=b\)。
首先有 \(a_{i+k}-a_i=b_{i+1}-b_i\)。那么将 \(i\) 和 \(i+k\) 合并,序列就变成了 \(\gcd(n,k)\) 个等价类(即环)。
如果有一个环里 \(b_{i+1}-b_i\ne 0\),那么环里所有 \(a\) 值都是固定的。如果所有 \(b\) 值都相等,那么 \(a\) 值就有两种可能:全 \(0\) 或者全 \(1\)。
现在假设有 \(t\) 个环所有 \(b\) 相等。如果我们选择 \(x\) 个环 \(a\) 值全 \(1\),那么每一个长度为 \(k\) 的子段的和(即 \(f(a)\) 的每一项的值)都会加上 \(x\times\frac{k}{\gcd(n,k)}\)。因为长度为 \(k\) 的子段在每个环里都有 \(\frac{k}{\gcd(n,k)}\) 个数。
所以,设 \(l=\gcd(n,k)\)。我们只考虑选择全 \(1\) 的个数,因此可以枚举 \(b\) 相等的环的个数,答案即为:
设 \(a=2^{\frac{n}{l}}-2\),利用 \(t\binom{l}{t}=\frac{l!}{(t-1)!(l-t)!}=l\binom{l-1}{t-1}\),可以化简式子:
代码:https://paste.ubuntu.com/p/V2dTNW2WnR/。
[ARC156C] Tree and LCS(构造 + 剥叶子)
很神奇的构造阿。
剥叶子,每次取出两个叶子 \(u,v\),令 \(p_u=v\),\(p_v=u\)。如果最后有剩余的一个节点就令其 \(p\) 值为它本身。
证明可以考虑归纳,见题解:https://atcoder.jp/contests/arc156/editorial/5777。
这题充分告诉我们做题需要想象力。
代码:https://paste.ubuntu.com/p/Wsmtp8shBR/。
2.23
2022.2.23 考试 T1 Easy Restrictions(easy)(DP)
题意:
对于给定的 \(n,k,c\),称一个序列 \(a\) 是好的当且仅当:
- \(a\) 中所有元素都是正整数。
- \(\sum\limits_{i=1}^{|a|}a_i=n\)。
- 恰好存在 \(k\) 组 \(l,r\) 满足 \(1\le l\le r\le |a|\) 且 \(\sum\limits_{i=l}^r a_i=c\)。
设 \(f(n,k,c)\) 表示对于给定的 \(n,k,c\) 有多少种好的序列。
给定 \(n,m,c\),你需要对每个 \(k\in[0,m]\) 求出 \(f(n,k,c)\)。答案对 \(998244353\) 取模。
数据范围:\(1\le c\le n\le 5\times 10^3,0\le m\le n\)。
先对 \(a\) 序列做一遍前缀和。问题就变成在 \(0\sim n\) 中选择若干个数(其中 \(0\) 和 \(n\) 必选),使得 \(\sum\limits_{i=0}^{n-c}[i\text{ is chosen}][i+c\text{ is chosen}]\)。
将 \(0\sim n\) 按照\(\bmod c\) 的取值分成 \(c\) 类,每一类的个数都是 \(\mathcal{O}(\frac{n}{c})\) 级别的。然后可以设 \(g_{i,j,0/1}\) 表示对于当前这一类里的前 \(i\) 个数,有 \(j\) 个 \(x\) 满足 \(x\) 和 \(x+c\) 都被选择,上一个是否被选择的方案数。转移是显然的。因为每一类的转移都相同所以只需要做一遍。对于 \(0\) 必选的情况比较特殊,可以钦定第一个必选然后重新跑一遍 DP。
最后就是要将这 \(c\) 类的 DP 值合并起来。设 \(f_{i,j}\) 表示考虑前 \(i\) 类,上式的值为 \(j\) 的方案数。转移就是一个背包。
时间复杂度 \(\mathcal{O}(n^2)\)。
代码:https://paste.ubuntu.com/p/gVGW8SKt58/。
[ARC156D] XOR Sum 5(DP)
非常神奇的一道题阿。
将所有运算在\(\bmod 2\) 意义下考虑。
使用生成函数的思想,考虑到 \(x\oplus x=0\),我们实际上就是要求所有满足 \([x^S](x^{A_1}+x^{A_2}+\dots+x^{A_N})^K\) 为 \(1\) 的 \(S\) 的异或和。
由 \((x_1+x_2+\dots+x_n)^2\equiv x_1^2+x_2^2+\dots+x_n^2+2\sum\limits_{i<j}x_ix_j\equiv x_1^2+x_2^2+\dots+x_n^2\) 推广可得 \((x_1+x_2+\dots+x_n)^{2^k}\equiv x_1^{2^k}+x_2^{2^k}+\dots+x_n^{2^k}\)。
所以假设 \(K=\sum\limits_{i=1}^M 2^{k_i}\)(\(k_i<k_{i+1}\)),就有 \([x^S](x^{A_1}+x^{A_2}+\dots+x^{A_N})^K\equiv[x^S]\prod\limits_{i=1}^M (x^{A_1\times 2^{k_i}}+x^{A_2\times 2^{k_i}}+\dots+x^{A_n\times 2^{k_i}})\)。
所求就被我们转化为:求所有 \(\sum\limits_{i=1}^M A_{X_i}\times 2^{k_i}\) 的 XOR。
还是按位考虑。从低到高考虑每一位,只考虑当前位以及更高位的取值。即设 \(dp_{i,j}\) 表示考虑到第 \(i\) 位,第 \(i\) 位及更高位的取值为 \(j\)(形式化的,就是 \(\lfloor\frac{1}{2^{i}}\sum\limits_{x=1}^M[k_x\le i]A_{X_x}\times 2^{k_x}\rfloor=j\))的方案数的奇偶性。假设 \(cnt=\sum\limits_{x=1}^M[k_x\le i]\),那么第 \(i\) 位后面填数的方案数为 \(n^{M-cnt}\)。如果这个方案数为奇数并且 \(j\) 为奇数,那么答案就可以异或上 \(2^i\)。
太神奇了,这个转换和 DP 都很神奇。
代码:https://paste.ubuntu.com/p/jSq3vNWkX4/。
[ABC290F] Maximum Diameter(构造 + 组合计数)
数组 \(X\) 合法的充要条件是:\(\forall 1\le i\le n,X_i\ge 1\);\(\sum X_i=2n-2\)。
构造最长的直径可以考虑直接拿出两个叶子,链上全部是 \(X_i>1\) 的点,然后直接用叶子补齐度数。
枚举叶子数量 \(i\),剩下的点度数之和为 \(2n-2-i\),且每个点度数 \(\ge 2\)。可以考虑将剩下 \(n-i\) 个点每个点的度数减去 \(1\),问题就变成:有 \(n-i\) 个数,每个数 \(\ge 1\),和为 \(2n-2-i-(n-i)=n-2\),求方案数。根据插板法可得答案为 \(\binom{n-3}{i-2}\)。
所以我们要计算的式子就是:
有以下恒等式:
- \(\binom{n}{r}=\frac{n}{r}\binom{n-1}{r-1}\);
- \(\sum\limits_{i=0}^n\binom{n}{i}\binom{m}{k-i}=\binom{n+m}{k}\)。
推式子:
代码:https://paste.ubuntu.com/p/FZwRsSQnW3/。
2023.2.23 考试 T2 Bubble Sort(bubble)(DP + 冒泡排序)
题意:
对于一个 \(1\sim n\) 的排列 \(a\) 和一个数 \(m\),定义 \(f(a,m)\) 为恰好经过 \(m\) 轮冒泡排序后变为 \(a\) 的不同排列数量。
一轮冒泡排序的过程如下:从小到大依次考虑每个 \(i\in[1,n)\),如果 \(a_i>a_{i+1}\) 就交换 \(a_i\) 和 \(a_{i+1}\)。
给定 \(n,m\) 和一个长度为 \(n\) 的序列 \(lim\)。一个排列 \(a\) 合法当且仅当 \(\forall i\),如果 \(lim_i\ne 0\),那么 \(a_i=lim_i\)。
求所有合法的 \(a\) 的 \(f(a,m)\) 之和对 \(998244353\) 取模的结果。
保证存在至少一个合法的排列 \(\mathbf{a}\)。
数据范围:\(1\le n\le 5\times 10^3,0\le m\le n\)。
关于冒泡排序有许多经典结论,比如:
- 设 \(cnt_i\) 表示序列里在 \(i\) 之前比 \(i\) 大的数,即 \(cnt_i=\sum\limits_{j=1}^{pos_i-1}[a_j>i]\),那么进行一轮冒泡排序之后 \(cnt_i\leftarrow\max(0,cnt_i-1)\)。
- 原排列和 \(cnt\) 数组一一对应。
所以我们可以直接对 \(cnt\) 数组计数。
后面可以直接参考官方题解。\(m!\) 是因为最大的 \(m\) 个数的 \(b\) 数组取值个数只有 \(1\sim m\) 个。

代码:https://paste.ubuntu.com/p/fv4qbjkBF5/。
2.24
2022.2.23 考试 T3 Softball(softball)(性质 + Trie 树)
题意:
给定 \(n\) 个数 \(a_{1\sim n}\)。
有 \(q\) 次询问,每次给定一个数 \(w\),你需要从左到右依次考虑每个数,设当前考虑到了第 \(i\) 个数,有以下两种决策:
- 跳过第 \(i\) 个数。
- 如果 \(w\ge a_i\),那么你可以将 \(w\) 变为 \(w\ \mathrm{xor}\ a_i\)。
对于每次询问,你需要求出最多能进行多少次第二种操作(即合并操作)。询问之间相互独立。
数据范围:\(1\le n\le 2\times 10^5,1\le m\le 10^6,1\le a_i,w<2^{30}\)。
题解已经很详细了:

补充一些要注意的地方:
- “如果第二类限制中存在 \(j,k\) 满足 \(j<k\) 且 \(hb(a_j)<hb(a_k)\),那么 \(j\) 产生的限制就没有用”,是因为异或 \(a_j\) 并不会改变比 \(hb(a_j)\) 更高的位的值,所以 \(k\) 的限制严格强于 \(j\) 的限制。
代码:https://paste.ubuntu.com/p/g8j4bPJvzd/。
[NWERC2019] K. Kitesurfing(DP + 模拟)
很神奇阿。不知道为什么最近有一种做的题都是神题的感觉。
观察 1:如果跳跃的一步的起点和终点都不是岛屿端点,那么我们可以通过不断将跳跃起点向左移动使得其中一个端点是岛屿端点。这样做和原方案显然是等价的。

观察 2:如果两点之间没有岛屿,那么有三种选择:只跳跃;跳跃若干步之后冲浪(显然最后冲浪的距离需要小于跳跃一步的距离);只冲浪。哪一种最优取决于两点间距离和跳跃时间。

考虑 DP,设 \(f_i\) 表示从 \(i\) 开始到终点的最短时间。
转移有两种:
-
跳到某个岛屿的右端点处。

-
跳到某个岛屿的左端点处,下一步跳到尽量远的地方。

因为能够到达的点的状态数是 \(\mathcal{O}(n^2)\) 的(从某个点的左/右端点到另一个点的左/右端点),所以总时间复杂度为 \(\mathcal{O}(n^3)\)。
代码:https://paste.ubuntu.com/p/MYcMnPKHFk/。
[QOJ3874] (Singapore)NOI2022 T4 Grapevine(点分树 + 树链剖分 + 线段树)
对于完全二叉树的部分分(子任务 3),注意到树的深度很小,因此考虑维护 \(f_i\) 表示 \(i\) 到 \(i\) 子树中最近的一盏亮着的灯的距离。对于所有操作都可以通过暴力跳祖先来更新 \(f\) 数组。
如果只有一次询问可以考虑点分治:求出 当前分治中心 \(rt\) 到 离它最近的亮着的灯 的距离 \(dis\),然后直接用 询问点到 \(rt\) 的距离 加上 \(dis\) 来更新答案。
对于多次询问,考虑建出点分树,然后在点分树上暴力跳祖先,并且对于每个点 \(u\),实时维护以它为分治中心的连通块里每个点到它的距离,以及它到最近的亮着的灯的最小距离。
具体的,对于点分树上的每个点建一棵线段树,大小为 以它为分治中心的连通块的大小。线段树的下标为 DFS 序,存储每个点到分治中心的距离,维护区间内所有亮着的灯到分治中心的最小距离。前两种操作都可以暴力跳祖先并且用基础线段树操作来维护,第三种操作只需要暴力跳祖先然后使用线段树区间加法。
代码:https://paste.ubuntu.com/p/BKYSwvYGqv/。
2.25
The 1st Universal Cup. Stage 5: Osijek 部分题目
2.26
2023.2.25 考试 T2 采购蔬菜(vege) / [COCI2021-2022#3] Akcija(A* + DP)
设状态 \((i,j)\) 表示前 \(i\) 个买了 \(j\) 个,\((i,j)\to(i+1,j)\) 连 \(0\) 边,\((i,j)\to(i+1,j+1)\) 连 \(w_{j+1}\) 边,问题转化成 \((0,0)\to(n,j=n\sim 0)\) 的前 \(k\) 短路径。
首先求出 \(g_{i,j}\) 表示 \((i,j)\) 到终点的最短路。
按层做,每层保留最优(按当前值 \(+g\) 排序)的前 \(k\) 优解。每个解向下一层最多有 \(2\) 条出边,答案就是最后一层的 \(k\) 个状态。
时间复杂度 \(\mathcal{O}(nk)\)。
启发:前 \(k\) 大 \(\to\) 考虑 A*。
2023.2.25 考试 T1 积木大赛ab(ab) / [POI2012] WYR-Leveling Ground(exgcd + 贪心 + 堆)
似乎场上除了差分都想到了(
考虑对原序列 \(a_{1\sim n+1}\) 差分,操作就变成选一个点 \(\pm a/b\)。对每个位置用 exgcd:
- \(d_i=ax+by\)。
- 最小化 \(|x|+|y|\)。
可以求出 \(x\) 为 最小非负整数 / 最大非正整数 和 \(y\) 为 最小非负整数 / 最大非正整数 的情况。容易发现 \(|x|+|y|\) 的最小值只有可能在这四种情况里出现。
还需要满足 \(\sum x=0\) 的条件。不妨假设 \(\sum x>0\),则需要调整 \(\sum\frac{x}{\frac{b}{\gcd(a,b)}}\) 次。调整一组 \((x,y)\) 的代价随着调整次数的增加是不降的(即它是个凸的),所以可以用小根堆贪心。
调整到 \(\sum x=0\) 之后 \(\sum y=0\) 同样成立。而调整次数是 \(\mathcal{O}(n)\) 量级的(证明见 https://www.luogu.com.cn/blog/AlexWei/solution-p3543)。所以总复杂度 \(\mathcal{O}(n\log n)\)。
2.27
[ARC157C] YY Square(组合计数 + DP)
似乎是一道很套路的题目……
对于平方和考虑增量,\((x+1)^2=x^2+2x+1\),所以我们可以记录 \(f_{i,j}\) 表示走到 \((i,j)\) 的所有方案的贡献的平方之和,\(g_{i,j}\) 表示走到 \((i,j)\) 的所有方案的贡献之和,而走到 \((i,j)\) 的方案数可以直接用组合数方便地求出来,即 \(\binom{i+j-2}{i-1}\)。
然后考虑怎么转移,显然只有 \((i,j)\) 是 Y 且 \((i,j-1)/(i-1,j)\) 也是 Y 才可以有增量的贡献。那么就直接按照那个增量的式子进行转移就可以求出答案。
代码:https://paste.ubuntu.com/p/CHRrMBwFMX/。
[ABC290G] Edge Elimination(贪心)
什么神仙贪心题……
枚举连通块深度最小的点(即连通块的“根”),然后考虑贪心,从大到小考虑所有子树大小,能删就删,正确性证明可见官方题解:https://atcoder.jp/contests/abc290/editorial/5810。
反正我是做不来。
代码:https://paste.ubuntu.com/p/2xfqd6GB6q/。
[ARC157D] YY Garden(性质 + 枚举)
牛题。
先求出网格里 Y 的总个数 \(su\)。显然 \(su\equiv 0\pmod 2\)。下面令 \(su\leftarrow\frac{su}{2}\)。
注意到一次在一行下面 / 一列右边分割的限制很强,考虑枚举横向分割的数量 \(h\),那么纵向分割的数量 \(w\) 就是 \(\frac{su}{h+1}-1\),需要满足 \(0\le h<n,0\le w<m\)。
显然相邻纵向分割之间需要有 \(2(h+1)\) 个 Y,相邻横向分割之间需要有 \(2(w+1)\) 个 Y。接下来可以线性扫一遍行 / 列来求出所有可能的分割位置。注意有可能有一段连续的区间满足(即这一段区间内除了第一个位置代表的行 / 列有 Y,其它位置代表的行 / 列中全部都是 X),这种划分的方案数就是所有区间长度的乘积。
最后还要判断一下是否每个分割出的小矩形里都有 \(2\) 个 Y。
时间复杂度 \(\mathcal{O}(nm+k(n+m+y))\)。其中 \(k\) 为所有满足条件的 \((h,w)\) 对数,\(y\) 为网格里 Y 的数量。在这个范围内 \(k\le 80\),\(ky\le 6.1\times 10^7\),所以可以通过。
代码:https://paste.ubuntu.com/p/NNPSXvj56m/。
[ABC288F] Integer Division(DP + 前缀和优化)
比较清新的一道题!
设 \(f_i\) 表示划分到 \(i\) 的所有方案的乘积之和。转移显然有 \(f_i=sub(1,i)+\sum\limits_{j=1}^{i-1}f_j\times sub(j+1,i)\),其中 \(sub(l,r)\) 表示 \([l,r]\) 这一段形成的数。
推一波式子:
显然可以前缀和优化转移。
代码:https://paste.ubuntu.com/p/Pg35NQ5RG6/。
[ABC288G] 3^N Minesweeper(容斥 + 高维前缀和 / Fast Zeta Transformation)
参考:https://www.cnblogs.com/Lanly/p/17094101.html & https://atcoder.jp/contests/abc288/editorial/5674。
核心思想就是按位来迭代容斥。具体可见上面的链接,我就不再赘述了。
代码:https://paste.ubuntu.com/p/hpYyS5sHy8/。
2.28
[ABC288Ex] A Nameless Counting Problem(组合计数 + DP)
我愿称之为计数神题。零零散散做了差不多 2h+(
定义合法序列为满足以下条件的序列:
- 其中每个元素都在 \([0,m]\) 中。
- 所有元素异或和为 \(x\)。
注意到如果 \(A_i=A_{i+1}\) 那么删去这两个元素对序列异或和不会有影响。所以假如能算出 \(g_i\) 表示长度为 \(i\) 的不包含重复元素的合法序列数量,则答案为:
先考虑如何求出合法序列的数量。设 \(f_i\) 表示长度为 \(i\) 的合法序列数量。按照 \(x\) 的二进制位从高到低进行 DP(类似数位 DP),设 \(dp_{i,j}\) 表示考虑了后 \(i\) 位,有 \(j\) 个数卡在 \(m\) 的上界的合法序列数量。转移直接枚举下面一位有多少个数还贴着上界,具体可见代码。那么 \(f_i=\sum\limits_{j=0}^{i}dp_{0,j}\)。
考虑计算 \(g_l\)。先令 \(g_l\leftarrow f_l\),再减去有重复元素的合法序列数量。
设:
- 序列中有 \(i\) 个出现了奇数次的元素;
- 序列中有 \(j\) 个出现了奇数次的数字;
- 序列中有 \(k\) 个出现了偶数次的数字。
再设:
- \(odd_{i,j}\) 表示将 \(i\) 个可区分的元素划分成 \(j\) 个不可区分的集合里,每个集合里元素个数为奇数的方案数。
- \(even_{i,j}\) 同理,表示每个集合里元素个数为偶数的方案数。
那么对于固定的 \((i,j,k)\),满足条件的序列数量为:
对于所有的 \(i\in[0,l],j\in[0,l-1],k\in[0,l]\),我们都将 \(g_l\) 减去上式,这样就可以求出所有的 \(g_l\) 了。
时间复杂度 \(\mathcal{O}(n^3\log m)\)。
代码:https://paste.ubuntu.com/p/TYqZCgb2mN/。
2023.2.28 考试 T1 吉他(guitar)(二分 + 最短路)
题意:
给定一张 \(n\) 个点 \(m\) 条边的简单无向连通图,你需要给每条边 \((u_i , v_i)\) 确定权值 \(h_i\),满足以下条件:
- \(h_i\) 均为 \([1, 10^{12}]\) 之间的正整数。
- \(h_{p_1} < h_{p_2} < \dots < h_{p_m}\),其中 \(p_{1\sim m}\) 是给定的 \(1 \sim m\) 的排列。换句话说,第 \(p_i\) 条边的权值 \(h_{p_i}\) 是所有权值中严格第 \(i\) 小的。
- \(S\) 到 \(T\) 的最短路恰好为 \(D\),其中 \(S, T, D\) 由输入给定。
判断是否存在这样的 \(h\),如果存在,构造一组合法的 \(h\)。
数据范围:\(2\le n\le 10^5,n-1\le m\le \min(2\times 10^5,\frac{n\times (n-1)}{2}),1\le D\le 10^{11}\)。图中不存在重边或自环且整
图连通。
首先把边权第 \(i\) 小的边的边权直接设为 \(i\)。如果这个时候 \(S\to T\) 的最短路长度比 \(D\) 大那么显然无解。
二分一个阈值 \(mid\),只考虑边权比第 \(mid\) 小的边权还小的边(即只考虑编号为 \(p_{1\sim mid}\) 的边),找到一个最小的 \(mid\) 使得 \(S\to T\) 的最短路还是 \(\le D\),那么修改 \(>mid\) 的边都没有效果,可以直接 \(+\infty\)。然后直接给第 \(mid\) 小的边的边权加 \(D-dis_{S\to T}\)。正确性显然。
代码:https://paste.ubuntu.com/p/2sMKDyjRnw/。
[CF1799G] Count Voting(容斥 + 背包)
设 \(cnt_i=\sum\limits_{j=1}^n[t_j=i]\)。
考虑容斥,枚举有 \(k\) 张票投给了自己团队的人。设有至少 \(d_i\) 张票是和 \(i\) 同一团队的人投给 \(i\) 的,剩下 \(c_i-d_i\) 张票随便。那么方案数为:
拆成阶乘形式:
这个可以直接背包做。具体的,即枚举每个团队里的每个人的 \(d\),然后用背包合并贡献。
代码:https://paste.ubuntu.com/p/26C7mq877d/。
[ABC287Ex] Directed Graph and Query(bitset 传递闭包 + Floyd)
考虑 Floyd 的过程,外层循环 \(k\) 实际上就是只考虑 \(1\sim k\) 的点进行中转。所以在 Floyd 的时候做传递闭包,然后扫描每组询问,找到一个最小的 \(k_i\) 使得 \(s_i\) 和 \(t_i\) 联通,那么这个询问的答案就是 \(\max(k_i,s_i,t_i)\)。
代码:https://paste.ubuntu.com/p/W8zWdR6RY2/。
3.1
三月了……
[ABC286G] Unique Walk(欧拉路径)
考虑将所有的一次性边断开,剩下的图会碎成若干个连通块。
由于其它边并没有通过次数限制,即可以在里面随便走,所以每个连通块可以抽象为一个点。
然后随便考虑一下在连通块内部,即两端点在同一个连通块的一次性边。
显然只要到了这个连通块就可以直接走掉,无需考虑。
然后我们现在拿到了一个无向图,要求找到一条路径走掉所有的边恰好一次。
显然这是欧拉路径问题,当奇数度点为 \(0\) 个或 \(2\) 个的时候为 Yes,否则为 No。
连通块的度数由于是奇偶性,可以直接并查集维护。
代码:https://paste.ubuntu.com/p/sRCQFdGdV7/。
[ABC290Ex] Bow Meow Optimization(贪心 + 性质 + DP)
因为数据范围很小,所以有退火做法。这里介绍官方题解的 DP 做法。
考虑最终最优解的结构肯定如下图所示:
其中箭头指向的方向是权值递增的方向,红圈是狗,蓝圈是猫。
证明考虑调整法,具体可见官方题解:https://atcoder.jp/contests/abc290/editorial/5814。
先将奇数的情况特判掉,然后就只需要考虑 \(n,m\) 都是偶数的情况。
将所有权值放在一起从小到大排序。
考虑直接 DP。设 \(f_{i,j,k}\) 表示已经考虑了前 \(i\) 小的权值,左半部分有 \(j\) 只狗和 \(k\) 只猫的最小不和谐度。转移直接枚举当前数是放在左边还是右边,贡献计算是平凡的。
代码:https://paste.ubuntu.com/p/H2w29qBHHQ/。
[ABC262Ex] Max Limited Sequence(DP + 线段树)
没看题解过了这题。感动。调了快一个小时没过的原因竟然是漏了一个取模。难蚌。
首先可以求出每个位置上的数的上限 \(mx_i\)。这个可以线段树区间 \(\min\) 单点查询解决。
然后把上限相同的数一起考虑,设当前考虑的上限为 \(val\)。
考虑 DP。设 \(f_i\) 表示已经填完了 \(1\sim i\),位置 \(i\) 填了上限的方案数。转移考虑枚举上一个达到上限的位置,\(f_i\leftarrow f_j\times val^{cnt(j+1,i-1)}\),其中 \(cnt(j+1,i-1)\) 表示 \([j+1,i-1]\) 中上限为 \(val\) 的数的个数。把所有最大值 \(=val\) 的区间 \([l,r]\) 拿出来,显然 \(j\) 满足条件当且仅当 \([j+1,i-1]\) 没有包含任何一个这样的区间 \([l,r]\)。可以直接二分 / 双指针找到 \(j\) 的下界 \(pmx_i\)。
容易发现转移是一个前缀和的形式:\(f_i=\sum\limits_{j\ge pmx_i} f_j\times val^{cnt(j+1,i-1)}\)。化简可得 \(f_i=val^{cnt(1,i-1)}\sum\limits_{j\ge pmx_i}\frac{f_j}{val^{cnt(1,j)}}\)。可以前缀和优化。
统计答案可以枚举最后一个达到上限的位置,那么它后面的数字都是随便填。
把所有上限得到的答案相乘就是总方案数。
代码:https://paste.ubuntu.com/p/K76c2jVSTs/。
跟“某位歌姬的故事”很像,所以就把那个题口胡掉了!
[ABC262G] LIS with Stack(区间 DP)
这怎么想得到???
考虑区间 DP。设 \(f_{i,j,mn,mx}\) 表示只考虑区间 \([i,j]\) 内的数,形成的值域在 \([mn,mx]\) 中的最长不降序列长度。
转移考虑 \(a_i\) 是否被插入栈中:
- 不被插入。从 \(f_{i+1,j,mn,mx}\) 转移而来。
- 被插入。枚举 \(a_i\) 是在 \(i+1\sim k\) 都被移动到序列里之后再被插入栈中的,从 \(1+f_{i+1,k,mn,a_i}+f_{k+1,j,a_i,mx}\) 转移而来。
答案即 \(f_{1,n,1,50}\)。
代码:https://paste.ubuntu.com/p/DyCdTwx2rP/。
感觉这种数据范围小的离谱还可以被简化为区间信息的就可以考虑区间 DP?
[ABC223H] Xor Query(线性基)
显然可以线段树维护区间线性基做到 \(\mathcal{O}(n\log n\log X)\)。
注意到没有修改,所以我们实际上可以维护每个前缀的线性基。
具体来说就是,线性基上的每一位我们都选择位置尽量靠右的数。
具体实现可以参考代码。时间复杂度 \(\mathcal{O}((n+q)\log X)\)。
代码:https://paste.ubuntu.com/p/yfJMQsSS8h/。
[IOI2021] 分糖果(线段树二分 + 性质)
把每个时刻糖果的数量画成折线。每次操作可以看成一段折线的平移。
核心在于相邻两次不同种类的“碰壁”在原折线上的体现就是极差 \(>c\),
具体懒得写了,看洛谷题解吧。
代码:https://paste.ubuntu.com/p/VTgGYxdBNp/。
3.2
[ABC285G] Tatami(上下界网络流 + 二分图)
将网格图黑白染色,先把所有只能用 \(1\times 1\) 覆盖的点删掉。问题就转化成所有为 \(2\) 的点必须和周围一个点匹配,为 ? 的点随意是否匹配,问是否存在一个方案。
正常二分图匹配建图,只需要将为 \(2\) 的点和源点 / 汇点相连的边的下界改为 \(1\),跑有源汇上下界可行流就行了。
代码:https://paste.ubuntu.com/p/kWsqwBtHQB/。
2023.3.2 考试 T1 铲车(forklift)(线段树 / 差分)
题意:
对于由 \([0,2^k)\) 映射到 \([0,10^{18}]\) 的函数 \(A,B\),定义 \(f(x)\):
\[f(x)=A_{x\bmod 2^k}\&B_{\lfloor\frac{x}{2^k}\rfloor} \]其中 \(f(x)\) 为由 \([0,2^k)\) 映射到 \([0,10^{18}]\) 的函数,\(\&\) 为按位与。
再给出 \(q\) 个形如 \(l_i,r_i,v_i\) 的限制,你需要构造函数 \(A,B\) 满足对于所有 \(i\),\(\forall j\in[l_i,r_i],f(j)=v_i\)。
数据范围:\(k\le 16,0\le v_i\le 10^{18},q\le 2\times 10^5\)。
对于每个限制,考虑直接把所有涉及到的 \(A_k,B_k\) 或上 \(v_i\)。最后对于每一个二进制位,如果某个限制的 \(v_i\) 这一位为 \(0\) 但是其区间内有一个数的 \(f(x)\) 这一位为 \(1\)(即它对应的 \(A,B\) 这一位都为 \(1\)),那么就说明无解。
注意 \(A,B\) 是有值域范围的。超过了直接输出 -1。
线段树 / 差分都可以解决这个问题。
代码:https://paste.ubuntu.com/p/7BqsfzhYTD/。
[ABC284G] Only Once(组合计数 + 推式子 + 递推)
我感觉没有那么简单啊,为什么是蓝题。
不难发现如果连边 \(i\to A_i\),那么图的每个连通块都是一棵内向基环树。
容易发现每个点的贡献都是一样的,因此只要考虑固定一个点的贡献。
考虑枚举它到环的距离 \(d\) 和环长 \(s\)。总贡献为:
设后半部分为 \(f(d)\),因为模数不固定所以考虑递推。
所以答案为:
代码:https://paste.ubuntu.com/p/gJPRS5dZQB/。
[CF1799F] Halve or Subtract(贪心)
有一些显然的性质:
- 如果 \(k_1=0/k_2=0\),那么我们肯定是选择最大的若干个数进行操作。
- 如果对一个数进行了这两种操作,那么肯定是先进行第一种操作,再进行第二种操作。
对每一个数设一个 \(0/1\) 二元组 \((x_i\in\{0,1\},y_i\in\{0,1\})\) 表示它是否进行了第一种 / 第二种操作。
结论:将所有数从小到大排序之后,最终的 \(0/1\) 二元组形态一定形如:
也就是分成了五段。
证明对于首尾两段是显然的,只需要考虑中间一定不会出现 \((0,1),(1,0),(0,1)\) 这样的子序列,因为这样一定不优,可以通过调整得到。具体略去。
做法是比较简单的,枚举中间那一个 \((0,1)\) 段的首尾,然后五段的长度就都可以得出来,贡献的计算可以直接前缀和。
代码:https://paste.ubuntu.com/p/s4cXptf22h/。
3.3
[AtCoder Educational DP Contest T] Permutation(排列计数 + DP + 前缀和优化)
排列计数的一种套路,复习一下。
设 \(f_{i,j}\) 表示已经填了前 \(i\) 个位置,最后一个位置的值在前 \(i\) 个里的相对大小为 \(j\),满足条件的排列数量。
转移:如果 \(s_{i-1}\) 为 <,那么 \(f_{i,j}=\sum\limits_{k=1}^{j-1}f_{i-1,k}\);否则 \(f_{i,j}=\sum\limits_{k=j}^{i-1}f_{i-1,k}\)。
前缀和优化转移即可。
代码:https://paste.ubuntu.com/p/N9rNn93sVn/。
[ABC282G] Similar Permutation(排列计数 + DP + 前缀和优化)
大概算上一题的加强版?
设 \(f_{i,j,a,b}\) 表示考虑完前 \(i\) 位,相似度为 \(j\),\(A_i\) 在前 \(i\) 个数里的相对大小为 \(a\),\(B_i\) 在前 \(i\) 个数里的相对大小为 \(b\) 的合法方案数。
转移分四种情况考虑。把式子写出来发现直接二维前缀和就行了。
时间复杂度 \(\mathcal{O}(n^4)\)。
代码:https://paste.ubuntu.com/p/fW99CSPwv7/。
[ABC282Ex] Min + Sum(最值分治 + 二分 + 前缀和)
对 \(A\) 进行最小值分治。考虑跨过最小值位置 \(mid\) 的区间,它们在 \(A\) 中的贡献都是这个最小值 \(val\)。接下来就只需要求有多少个跨过 \(mid\) 的区间满足 \(B\) 数组中这个区间的和 \(\le S-val\)。可以枚举较短的那一边的一个端点,另一个端点可以二分 + 前缀和求出。
代码:https://paste.ubuntu.com/p/3TK5nqyYdQ/。
[ABC281G] Farthest City(BFS 树 + DP + 组合计数)
看到最短距离,想到 BFS 树。
考虑一棵以 \(1\) 为根的 BFS 树。显然有连边的点的层数差不超过 \(1\)。
设 \(f_{i,j}\) 表示前若干层已经确定了 \(i\) 个点,当前这一层有 \(j\) 个点的合法方案数。
转移枚举上一层的点数 \(k\),有:
注意当 \(i=n\) 时只有 \(j=1\) 时有值,所以需要特判一下转移。
代码:https://paste.ubuntu.com/p/cJGhdDFyYh/。
2023.3.3 考试 T2 巴士(bus)(二分 + 贪心 + Monitor 算法)
题意:
数轴上有 \(n\) 个闭区间 \([l_i,r_i]\),你需要通过给每个区间移动若干个单位长度使得这些区间能够覆盖 \([0,m]\),最小化区间移动的距离的最大值。
数据范围:\(1\le n\le 2\times 10^5,1\le m\le 10^9,0\le l_i\le r_i\le 10^9\)。
显然答案具有可二分性。因此二分答案 \(mid\)。
当 \(mid\) 已经给定时,我们可以使用如下贪心算法。
设 \(nowr\) 表示当前覆盖到的最远位置(注:算法运行过程中保证 \([0,nowr]\) 已经被覆盖)。
如果 \(nowr<m\):
- 假定当前未被使用过的区间为 \(D_1 ,\dots,D_K\)。
- 在这些区间中找一个在 \([-mid,+mid]\) 这个移动量内能覆盖点 \(nowr\) 的区间出来——如果有多个这样的区间,则选其中右端点最小的那一个。
- 不防假定 \(D_1\) 是所选的区间。那么,我们使用 \(D_1\) 来覆盖 \(nowr\)。具体做法为:移动 \(D_1\) 使得在保证 \(nowr\) 点被它覆盖的前提下移动后的位置越靠右越好!
- 把区间 \(D_1\) 标记为已使用过并且更新 \(nowr\) 为 \(D_1\) 移动后的右坐标。
证明似乎可以调整。这个算法叫 Monitor 区间覆盖。实质就是一个贪心。
有论文:Danny Z. Chen Yan Gu Jian Li Haitao Wang, Algorithms on Minimizing the Maximum Sensor Movement forBarrier Coverage of a Linear Domain。
代码:https://paste.ubuntu.com/p/d6w9sftHgC/。
3.4
2023.3.3 考试 T1 药(drink) / [CEOI2015 Day2] 核能国度(差分 + 前缀和 + 细节)
观察到 \(\max(|r-x_i|,|c-y_i|)\) 是切比雪夫距离,意味着一个药对矩形中格子的贡献形如一圈一圈的「回」字。
1 1 1 1 1 1 1 1 2 2 2 2 2 1 1 2 3 3 3 2 1 1 2 3 4 3 2 1 1 2 3 3 3 2 1 1 2 2 2 2 2 1 1 1 1 1 1 1 1差分后,先修改「回」字的四个角,即加上「回」字边上的值。中间的差分后是加两条对角线,当没有与矩形相交时是容易再差分一次维护的。
容易发现一个简单 \(O(n\sqrt{RC})\) 的做法,因为 \(R\cdot C\le 10^6\),所以 \(\min(R,C)\le 10^3\),不妨设 \(R\le C\),可以枚举每一行,再计算每一个药对这一行的贡献,直接差分细节较少。
下面是线性做法。考虑相交之后对角线等价于会变成什么样:
. . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ # # # # # . . . . . . . . @ # # # # . . . . . . . . @ . . . # . . . . . . . . @ . . . # . . . . . . . . # @ . . # . . . . -> . . . . # @ . . # . . . . . . . . # . @ . # . . . . . . . . # . @ . # . . . . . . . . # # # @ # . . . . . . . . # # # @ # . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . # # @ # # . . . . . . . . @ @ # # # . . . . . . . . # . . @ # . . . . . . . . # . @ . # . . . . . . . . # . . . @ . . . . -> . . . . # . . @ # . . . . . . . . # . . . # @ . . . . . . . # . . . @ . . . . . . . . # # # # # . @ . . . . . . # # # # # . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . # # @ # # . . . . . . . . # # @ @ @ . . . . . . . . # @ . . # . . . . . . . . # @ . . # . . . . . . . . @ . . . # . . . . -> . . . . @ . . . # . . . . . . . @ # . . . # . . . . . . . . @ . . . # . . . . . . @ . # # # # # . . . . . . . . @ # # # # . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . # # # # # . @ . . . . . . # # # # # . . . . . . . . # . . . # @ . . . . . . . # . . . # . . . . . . . . # . . . @ . . . . -> . . . . # . . . @ . . . . . . . . # . . @ # . . . . . . . . # . . @ # . . . . . . . . # # @ # # . . . . . . . . # # @ # # . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . . . . @ . . . . . . . . . . . . . . . . . . . . . .(注:"#" 是矩形边界,"@" 是对角线)
可能比较抽象,大概是会在边界新形成一些连续段。
注意上面第一二种情况可能需要修改矩形左上角,实现时细节较多。具体就是维护行、列、主对角线和副对角线的差分数组。
然后大力讨论就可以做到 \(O(RC+n+Q)\)。
可能有点卡空间,vector 空间消耗极大,可以把矩阵映射到一维数组里去做。
代码:https://paste.ubuntu.com/p/Yr4BJmpFd2/。
2023 NOI 春季测试 T1 T2
3.5
THUPC2023 部分题目
2023.3.3 考试 T3 同构(iso)(枚举 + DP + 费用流)
题意:
有一棵 \(n\) 个点的无根树,每条边形如 \((u_i, v_i)\)。
小 Z 和小 H 分别取出树上的一个子连通块,满足:
- 两个人没有取出同一个点。
- 两个人的子连通块同构。
小 Z 想要取出最多的点,请你告诉 TA 最多能取出多少个点。
数据范围:\(1\le n\le 60\)。
题解:
首先由于两个集合没有交,因此我们枚举树上每一个点 \(x\) ,假设点 \(x\) 为其中一个集合中深度最小的点,并删去点 \(x\) 连向父节点的这条边。
然后我们在点 \(x\) 父节点所在连通块中枚举一个点 \(y\) ,并假设在点 \(x\) 在另外一个集合中是与点 \(y\) 匹配同构,然后我们在另外一个连通块内以点 \(y\) 为根。
设 \(dp_{i,j}\) 表示在点 \(x\) 所在连通块内的点 \(i\) 和在点 \(y\) 所在的连通块内的点 \(j\) 匹配同构的最大点集大小,计算 \(dp_{i,j}\) 时我们需要将点 \(i\) 的若干儿子节点和点 \(j\) 的若干儿子节点进行匹配。
可以发现这个匹配的过程实际上就是一个二分图最大权匹配,使用 KM 算法或者最大费用最大流计算即可。
时间复杂度 \(O(n^5)\) 或 \(O(n^6)\) ,实际效率非常高。
代码写起来比较顺手:https://paste.ubuntu.com/p/3HJhdjKGHX/。
[ABC279G] At Most 2 Colors(DP + 前缀和优化)
我感觉是很神仙的题啊,怎么只有 *2431?????
设 \(dp_{i,1/2}\) 表示到第 \(i\) 个位置,最后 \(k-1\) 个位置(如果不足就是所有位置)有 \(1/2\) 种颜色的方案数。
为什么不是最后 \(k\) 个?因为这样设状态可以方便转移。已知 \(i-1\) 之前 \(k-1\) 个位置的颜色,那么考虑到 \(i\) 就是前 \(i\) 个位置的颜色了。
转移大概就是枚举上一个不同颜色的位置,具体情况自己分析就是了,可以看洛谷题解区。
答案即为 \(dp_{n,1}+dp_{n,2}\)。
代码:https://paste.ubuntu.com/p/Ky8MQBWP54/。
3.6
2023.3.6 考试 T1 皇帝的园林(garden) / [IOI2019] 矩形区域(单调栈 + 扫描线 + 树状数组)
我们称一条线段 \([l,r]\) 是合法的,当且仅当 \(l\sim r\) 中的最大值 \(mx\) 比 \(l-1\) 和 \(r+1\) 位置上的值都要小。
考虑先求出每一行 / 列的所有合法线段。
注意到只有线段中的数的最大值是有用的,所以可以考虑枚举最大值的位置,找到它左边和右边第一个比它大的位置 \(L,R\),那么 \([L+1,R-1]\) 就是一个合法线段。这个可以用单调栈求。
由这种求法我们可以知道,合法线段的总条数是 \(\mathcal{O}(nm)\) 的!
对于每一条合法线段,可以扫一遍求出它向下 / 向右最多能扩展多少(即向下若干行 / 向右若干列的 \([l,r]\) 还是合法线段),设为 \(dn_{i,j}/rt_{i,j}\)。
考虑枚举子矩形的上边界,显然它需要是一条合法线段。假设它的长度为 \(y\),它能向下扩展的长度为 \(x\),枚举以其左端点为上端点的向下的一条合法线段,把它当作左边界,那么这条线段应该满足长度 \(\le x\) 并且向右扩展的长度 \(\ge y\)。
把式子写出来大概是 \(rt_i\ge len_j,len_i\le dn_j\) 的形式,可以直接扫描线做。具体可以看代码。
时间复杂度 \(\mathcal{O}(nm\log nm)\)。
代码:https://uoj.ac/submission/609880。
[ABC277Ex] Constrained Sums(2-SAT + 构造)
似乎是一道很套路的题目,但是我不会/kk
因为 \(nm\le 10^6\),所以可以考虑对每个数 \(i\) 设 \(m+2\) 个 \(0/1\) 变量 \(v_{i,j}=[x_i\ge j]\)。强制 \(v_{i,0}=1,v_{i,m+1}=0\),然后考虑一些 2-SAT 的操作。
有结论:
- \(x_i+y_i\ge L\iff \forall t\in \mathbb{Z},x_i\ge t\lor y_i\ge L+1-t\);
- \(x_i+y_i\le R\iff \forall t\in\mathbb{Z},x_i<t\lor y_i\le R+1-t\)。
证明可以考虑反证法,感性理解就是如果 \(x_i+y_i\) 不满足条件那么一定可以找到一个 \(t\) 不满足后面的条件。
那么就可以连边了:
- \(x_i<t\Rightarrow y_i\ge L+1-t\);
- \(y_i<L+1-t\Rightarrow x_i\ge t\);
- \(x_i\ge t\Rightarrow y_i<R+1-t\);
- \(y_i\ge R+1-t\Rightarrow x_i<t\)。
代码:https://paste.ubuntu.com/p/fJv52wTWqd/。
2023.3.6 考试 T2 皇帝的多项式(polynomial) 80 分做法 / [LOJ577]「LibreOJ NOI Round #2」简单算术(递归 + k 进制拆分)
官方题解:https://loj.ac/d/1779。
假设最终第 \(i\) 次项有 \(b_i\) 次贡献,那么显然 \(\sum\limits_{i=0}^{n}b_i=m\),\(\sum\limits_{i=0}^n i\times b_i=k\)。
如果已知 \(b_i\),那么方案数为 \(\prod\limits_{i=0}^n\binom{m-\sum\limits_{j=0}^{i-1}b_j}{b_i}\bmod p\)。
若 \(m\) 是 \(p\) 的倍数,那么根据 Lucas 定理,如果方案数非零就需要所有 \(b_i\) 都是 \(p\) 的倍数,进而 \(k\) 也是 \(p\) 的倍数。
设 \(f(m,k)\) 表示答案,那么当 \(p|m\) 时,若 \(p|k\),那么 \(f(m,k)=f(\frac{m}{p},\frac{k}{p})\);否则 \(f(m,k)=0\)。
设 \(m=pa+b\),那么 \(f(m,k)=\sum\limits_{i=0}^kf(pa,i)\times f(b,k-i)\)。
容易发现最多只有 \(\min(\frac{k}{p},n(p-1))\) 个位置有值,所以 \(f(m,k)=\sum\limits_{k|i}f(a,\frac{i}{k})\times f(b,k-i)\),只有 \(\log_pm\) 层。
时间复杂度 \(\mathcal{O}(n^2p^2+Tn^2\log_pm)\)。
[ABC277G] Random Walk to Millionaire(期望 DP)
为什么 *2491 是蓝题啊???????
考虑期望 DP。注意到 \(E((x+1)^2)=E(x^2)+2E(x)+1\),所以可以考虑将这三部分拆开分别 DP。
设 \(p_{i,j}\) 表示走了 \(i\) 步到达点 \(j\) 的概率,\(dp_{i,j}\) 表示走了 \(i\) 步到达点 \(j\) 的等级的期望,\(dp2_{i,j}\) 表示走了 \(i\) 步到达点 \(j\) 的等级的平方的期望。
转移有:
如果 \(c_j=1\):
如果 \(c_j=0\):
答案可以在所有 \(c_j=1\) 的 \(j\) 处求 \(dp2_{i,j}\times p_{i,j}\) 的和来得到。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号