AtCoder Beginner Contest 288
A - Many A+B Problems (abc288 a)
题目大意
给定\(A\), \(B\),输出 \(A+B\)。
解题思路
范围不会爆\(int\),直接做即可。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int t;
cin >> t;
while(t--){
int a, b;
cin >> a >> b;
cout << a + b << '\n';
}
return 0;
}
B - Qualification Contest (abc288 b)
题目大意
给定排名前\(n\)的姓名,要求将排名前\(k\)的名字按字典序从小到达输出。
解题思路
范围不大,直接排序输出即可。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, k;
cin >> n >> k;
vector<string> s(n);
for(auto &i : s)
cin >> i;
sort(s.begin(), s.begin() + k);
for(int i = 0; i < k; ++ i)
cout << s[i] << '\n';
return 0;
}
C - Don’t be cycle (abc288 c)
题目大意
给定一张无向图,要求删除一些边,使得没有环。
解题思路
根据定义,无环就是一棵树或者森林。
对原图跑一遍最小生成树,不在该树的边都是要删去的。
故答案就是总边数减去最小生成树的边数。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
class dsu {
public:
vector<int> p;
vector<int> sz;
int n;
dsu(int _n) : n(_n) {
p.resize(n);
sz.resize(n);
iota(p.begin(), p.end(), 0);
fill(sz.begin(), sz.end(), 1);
}
inline int get(int x) {
return (x == p[x] ? x : (p[x] = get(p[x])));
}
inline bool unite(int x, int y) {
x = get(x);
y = get(y);
if (x != y) {
p[x] = y;
sz[y] += sz[x];
return true;
}
return false;
}
};
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m;
cin >> n >> m;
dsu d(n);
int ans = 0;
for(int i = 0; i < m; ++ i){
int u, v;
cin >> u >> v;
-- u;
-- v;
if (d.unite(u, v))
++ ans;
}
cout << m - ans << '\n';
return 0;
}
D - Range Add Query (abc288 d)
题目大意
给定一个数组\(A\)和\(k\),定义一个数组是好数组,当且仅当可经过若干次以下操作,使得数组全变成 \(0\)。
- 选定一个长度为\(k\)区间,令区间里的数都加上\(x\), \(x\)是自己选的
有 \(q\)个询问,每个询问包括 \(l,r\),问 \(A[l:r]\)是否是好数组。
解题思路
感觉这题难度\(>>E,F\)
因为涉及到区间加操作,一开始考虑差分数组,最终情况就是全部数为\(0\)。这样每次操作就只修改两个数,且观察到其下标对 \(k\)取模都是相同的。 然后考虑对原数组求一遍操作影响,看看子数组能否利用原数组的信息,思考了下感觉可行但代码复杂。
后来又退回思考原数组,因为是连续的区间加,假设\(sum[i]\)表示下标对 \(k\)取模为 \(i\)的所有数的和。那每次操作就是将 \(sum\)的所有数都 \(+x\)。那最终为 \(0\)的充分条件就是 \(sum\)的所有数都是一样的。反过来,也是必要条件。
因此对于每组询问,统计该序列的下标对\(k\)取模的所有数的和,看看是否为同一个数即可。
预处理原数组的下标取模前缀和,每组询问就两个前缀和相减就得到该区间的下标取模前缀和。因为\(k\)只有 \(10\),所以每次询问的复杂度就是 \(O(k)\)
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, k;
cin >> n >> k;
vector<LL> a(n);
for(int i = 0; i < n; ++ i){
cin >> a[i];
if (i >= k)
a[i] += a[i - k];
}
int q;
cin >> q;
while(q--){
int l, r;
cin >> l >> r;
-- l;
-- r;
vector<LL> tmp(k);
for(int i = 0, pos = r; i < k; ++ i, pos --){
tmp[pos % k] = a[pos];
}
for(int i = 0, pos = l - 1; i < k && pos >= 0; ++ i, pos --){
tmp[pos % k] -= a[pos];
}
cout << (set<LL>(tmp.begin(), tmp.end()).size() == 1 ? "Yes" : "No") << '\n';
}
return 0;
}
E - Wish List (abc288 e)
题目大意
给定\(n\)个商品的价格 \(a_i\) ,标号\(1\)到 \(n\)。你要买\(m\)个物品,分别是 \(x_i\)。同时给定一个数组 \(c\)。购买规则为:
- 购买序号为\(i\)的商品,其标号是未买商品的第\(j\)小,其购入价格为 \(a_i+c_j\)。
你可以买不需要的物品。
问购买所需物品的最小花费。
解题思路
考虑暴力,发现不仅要确定购买哪些商品,还需要规定购买这些商品的顺序。不同顺序代价会不一样(购买同一间商品的\(c_j\)可能因购买顺序而不同)
再考虑暴力搜索过程中,当确定购买一个物品的代价时,需要知道一个物品的标号是目前第几小的。知道这两个状态后发现可以切割子问题,因此考虑\(dp\)。
一开始考虑 \(dp[i][j]\)表示前\(i\)个物品,其第\(i\)个物品的标号是第 \(j\)时的最小花费,转移就考虑该物品买或不买,当然如果是必须要买的物品就不能不买。但这个状态有问题,就是它规定了购买的顺序一定是标号从小到大的。而这显然不对。
那就不能设第j小这样的状态,但转移的话需要知道物品标号排名,所以考虑另一个状态,即 \(dp[i][j]\)表示前\(i\)个物品,已经购买了 \(j\)个物品的最小花费,因为知道了买了\(j\)个物品,就知道下一个要买的物品的标号是第几小的。
这状态看似和之前一样,但转移有点不同:当我决定买第\(i\)个物品时,已知状态是购买了\(j\)个物品,但不一定第 \(i\)个物品是购买的第 \(j+1\)件(它可以是之前购买的,注意,标号大的物品先买不会影响到标号小的物品的选择,即后来的决策不会影响先前的结果),因此其附加代价\(c\)的值可以是 \(c_{i-j+1},c_{i-j+2},\cdots ,c_{i}\),选择不同的 \(c\)值 就是规定其购买的顺序。为了最小代价,那肯定是取最小的那个\(c\)。
因此转移式就是:
当然如果是该物品必须买的话,就没有后面\(dp_{i-1, j}\)这一项。
转移式涉及区间最小值,可以事先预处理或者转移时递增维护。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL inf = 1e18;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m;
cin >> n >> m;
vector<LL> a(n), c(n);
for(auto &i : a)
cin >> i;
for(auto &i : c)
cin >> i;
vector<int> must(n);
for(int i = 0; i < m; ++ i){
int x;
cin >> x;
-- x;
must[x] = 1;
}
vector<LL> dp(n + 1, inf);
dp[0] = 0;
for(int i = 0; i < n; ++ i){
vector<LL> tmp(n + 1, inf);
LL minn = inf;
for(int j = 0; j <= i; ++ j){
minn = min(minn, c[i - j]);
tmp[j + 1] = min(tmp[j + 1], dp[j] + a[i] + minn);
if (!must[i])
tmp[j] = min(tmp[j], dp[j]);
}
dp.swap(tmp);
}
LL ans = *min_element(dp.begin(), dp.end());
cout << ans << '\n';
return 0;
}
F - Integer Division (abc288 f)
题目大意
给定一个\(n\)位数\(s\)。 其有 \(n-1\)个切割点,一种切割方案包括若干个切割点,其代价是,切割后的所有数字的乘积。
问所有的\(2^{n - 1}\) 种切割 方案的代价和。
解题思路
经典切分数字题,从爆搜的角度发现问题可切割,考虑\(dp\)。
设 \(dp[i]\)表示前 \(i\)个数的的所有切割方案的代价和,转移就是枚举最后一个切割点位置。
其转移式为(这里假设下标从\(1\)开始,\(dp[0] = 1\)):
转移是\(O(n)\),总的复杂度是 \(O(n^2)\)。暂且过不了,考虑优化转移。
考虑 \(dp[i]\)和\(dp[i+1]\)的转移式,发现两者非常相似,只需一点改动就可以转移。
可以发现两者只有\(s[j+1:i]\)变成 \(s[j+1:i+1]\)的 ,相当于原来的转移和,乘以\(10\),然后加上\(\sum_{j=0}^{i - 1} dp_{j}\)个\(s[i + 1]\),再补上多的一项 \(dp_i \times s[i + 1]\)就变成\(i+1\)的转移和了。
因此转移可以优化成 \(O(1)\),最终的复杂度就是 \(O(n)\)
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const LL mo = 998244353;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n;
string s;
cin >> n >> s;
LL ans = 0;
LL presum = 1;
for(int i = 0; i < n; ++ i){
int val = s[i] - '0';
ans = (ans * 10 + presum * val) % mo;
presum = (presum + ans) % mo;
}
cout << ans << '\n';
return 0;
}
G - 3^N Minesweeper (abc288 g)
题目大意
众所周知,在著名的扫雷游戏里,格子上有个数字,表示该格子的邻居中有炸弹的数量。注意一个格子最多只有一个炸弹。
但这里有\(3^n\)个格子,标号\(0\sim 3^n - 1\),且格子\(i\)与格子 \(j\)相邻,当且仅当:
- 标号\(i\)和 \(j\)在三进制表示下,每个数位的值的
差的绝对值不超过\(1\)。
现给定每个格子邻居的炸弹数量\(a_i\),求每个格子的炸弹数量\(b_i\)。
解题思路
设\(i\)的三进制表示为: \(t_{n-1}\cdots t_1t_0\),\(a_i\)则表示成\(a(t_{n-1},\cdots ,t_1,t_0)\)。
由题定义的邻居关系,可得
我们已知左边的值,要求右边的每一项,这显然是个容斥。
但观察到求和条件是个差的绝对值这一非常规条件,直接反演难度非常大似乎反不动。
但这是数位上的条件,各个数位是独立的,我们尝试迭代数位的方式进行容斥。
考虑最简单的情况\(n=0\),即三进制表示下只有一位,很显然根据容斥,容易得到:
- \(b(0) = a(1) - a(2)\)
- \(b(1) = a(0) + a(2) - a(1)\)
- \(b(2) = a(1) - a(0)\)
这里其实忽略了高位,以第一个式子为例,可以看成:
- \(b(x_{n-1},\cdots,x_1,0) = a(x_{n-1},\cdots,x_1,1) - a(x_{n-1},\cdots,x_1,2)\)
但此时的\(b\)还不是答案的 \(b\),该项的意义是:最低位是 \(0\), 其余位是\(a\)数组意义的炸弹数。
但我们以上述的 \(b\)的结果,对 \(x_1\)进行同样方法的容斥,就得到 \(x_1,x_0\)是 其值的,其余位是\(a\) 数组意义的值。由此迭代的方式容斥,就能得到答案\(b\)数组。
以官方题解的说法,每个数位有六种情况,已知的是由前三种情况组成的值,通过迭代容斥,能逐步得到由后三种情况组成的值。
这其实非常类似于fast Zeta transformation
我们设\(a(t_{n-1},\cdots ,t_1,t_0, i)\)表示:低\(i\)项是精确的(就是该值),剩下的项是满足邻居条件的那些格子的炸弹数。
那么\(a(t_{n-1},\cdots ,t_1,t_0, i)\)可以由\(a(t_{n-1},\cdots ,t_1,t_0, i - 1)\)得到,针对第\(i\)项进行容斥。
而fast Zeta transformation又名子集和\(dp\)(SOS DP, sum over subset),为了不重复计算,通过额外的一个信息 \(i\),将前 \(i\)位定义为精确值,后面的位定义为其子集(题目意义)的值,然后通过迭代计算得出\(i=0\)的结果。
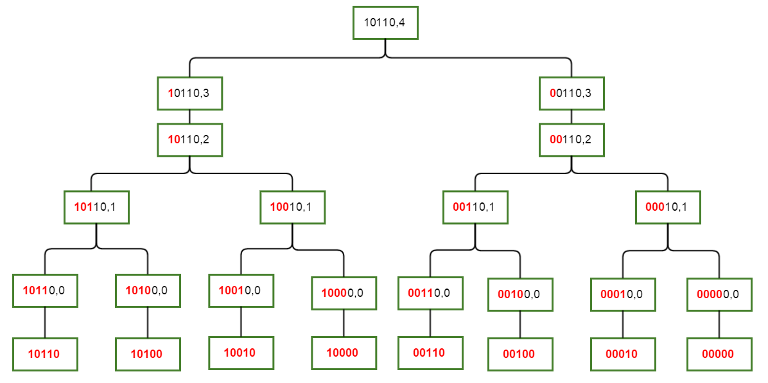
观察上面的图,每个节点的红色部分就是精确的,黑色部分是模糊的(子集的),其代表的值(所有叶子)就是黑色部分的所有子集的和。
当然本题是已知所谓子集,求每个精确项的值,是个逆过程,其实是一样的,只是每次迭代由相加变成了容斥。但不变的是以迭代的方式求解(其实这也是FZT的核心,具体每次迭代怎么计算因题而异)。
总的复杂度就是\(O(n3^n)\)
代码实现的话,简单一点就是考虑对\(a(t_{n-1},\cdots ,t_1,t_0, i)\)的计算,已知的是\(i=0\)(全部都不是精确)的值,最终要求的就是 \(i=n\)(全部是精确)的值。
- \(a(t_{n-1},\cdots,t_{i}, 0 ,t_{i-2},\dots,t_1,t_0, i) = a(t_{n-1},\cdots,t_{i}, 1 ,t_{i-2},\dots,t_1,t_0, i - 1) - a(t_{n-1},\cdots,t_{i}, 2 ,t_{i-2},\dots,t_1,t_0, i - 1)\)
- \(a(t_{n-1},\cdots,t_{i}, 1 ,t_{i-2},\dots,t_1,t_0, i) = a(t_{n-1},\cdots,t_{i}, 0 ,t_{i-2},\dots,t_1,t_0, i - 1) + a(t_{n-1},\cdots,t_{i}, 2 ,t_{i-2},\dots,t_1,t_0, i - 1) - a(t_{n-1},\cdots,t_{i}, 1 ,t_{i-2},\dots,t_1,t_0, i - 1)\)
- \(a(t_{n-1},\cdots,t_{i}, 2 ,t_{i-2},\dots,t_1,t_0, i) = a(t_{n-1},\cdots,t_{i}, 1 ,t_{i-2},\dots,t_1,t_0, i - 1) - a(t_{n-1},\cdots,t_{i}, 0 ,t_{i-2},\dots,t_1,t_0, i - 1)\)
因为每次都是用到的都是\(i-1\),因此最后一维可以压缩掉(压缩掉的话注意转移时引用计算的是正确的数),以及前\(n\)项通过三进制压缩程一个数。
神奇的代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
int main(void) {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n;
cin >> n;
vector<int> p3(n + 1);
p3[0] = 1;
for(int i = 1; i <= n; ++ i)
p3[i] = p3[i - 1] * 3;
vector<int> a(p3[n]);
for(auto &i : a)
cin >> i;
for(int i = 0; i < n; ++ i){
int p = p3[i];
for(int j = 0; j < p3[n]; ++ j){
if ((j / p) % 3 == 0){
int a1 = j, a2 = a1 + p, a3 = a2 + p;
int v1 = a[a1], v2 = a[a2], v3 = a[a3];
a[a1] = v2 - v3;
a[a2] = v1 + v3 - v2;
a[a3] = v2 - v1;
}
}
}
for(int i = 0; i < p3[n]; ++ i)
cout << a[i] << " \n"[i == p3[n] - 1];
return 0;
}
Ex - A Nameless Counting Problem (abc288 h)
题目大意
<++>
解题思路
<++>
神奇的代码


 浙公网安备 33010602011771号
浙公网安备 33010602011771号