A

方法一 : 暴力判断枚举子串，判断其是否回文，O( $\frac 14n^3$)

方法二 : 整个串已知是一个回文串，贪心地想前 $n - 1$ 构不构成回文串 , 若不构成 , 则答案就是 $n - 1$
若前 $n - 1$ 构成回文，且 $n$ 构成回文串，类似于 $s[n] = s[1] = s[n - 1] = s[2] ... $ , 全串都相同

#include <bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0) ; cout.tie(0);
	int t;
	cin >> t;
	while(t--){
		string s;
		cin >> s;
		map<char,bool> ma;
		for(int i = 0 ; i < s.length() ; ++i)
			ma[s[i]] = true;
		if(ma.size() == 1) cout << "-1\n";
		else cout << s.length() - 1 << '\n'; 
	} 
	return 0;
}

B

考虑对全局影响最大的几个点 $ (1,1) , (1,2) , (2 , 1) $
所有 $x \geqslant 2 , y \geqslant2 $ 的矩阵均能受到最大值 - 最小值的影响 , 那么对于 $ x\leqslant 1$ 或者 $ y\leqslant 1$ 的的矩阵只能只能选择其一（选择个数最多的行或列）受到最大值 - 最小值的影响，剩下的一行或者列受到 $ max ( 最大 - 次小 , 次大 - 最小 ) $ 的影响

#include <bits/stdc++.h>
using namespace std;
#define ll long long

int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0) ; cout.tie(0);
	int t;
	cin >> t;
	while(t--){
		int n,m;
		cin >> n >> m;
		vector<int> a(n * m);
		for(int i = 0 ; i < n * m ; ++i)
			cin >> a[i];
		sort(a.begin(),a.end());
		if(n < m) swap(n , m);
		ll ans = 1ll * (a[n * m - 1] - a[0]) * (n * m - m) + 1ll * (m - 1) * max(a[n * m - 1] - a[1] , a[n * m - 2] - a[0]);
		cout << ans << '\n';
	}	
	return 0;	
}

C

考虑可以确定的位置和不确定位置( $-1 , -2$ )的优先级问题 , 确定位置对于不确定位置的影响是不确定位置只能放在确定位置(最左 , 最右)的左边和右边 , 不确定位置对于确定位置的影响是不确定位置会占据确定位置 , 这里我们应该会想到经典的 "填充" 的策略 , 固定一个位置 x , 往它左右两边填确定位置 , 确定位置中间填充不确定位置即可 , 这样坐标递增递减地填尽可能地减少了 "最左" , "最右"限制的影响.

同时要考虑其他情况 : 一开始填 $-1$ 或 $-2$

#include <bits/stdc++.h>
using namespace std;
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0) ; cout.tie(0);
	int t;
	cin >> t;
	while(t--){
		int n,m;
		cin >> n >> m;
		vector<int> a(n) , b;
		int res1 = 0 , res2 = 0 , ans;
		for(int i = 0 ; i < n ; ++i){
			cin >> a[i];
			if(a[i] == -1) ++res1;
			else if(a[i] == -2) ++res2;
			else b.push_back(a[i]);
		}
		sort(b.begin(),b.end());
		b.erase(unique(b.begin(),b.end()),b.end());
		ans = min(max(res1 , res2) + (int)b.size() , n); //一开始填 -1 或者 -2 
		for(int i = 0 ;i < b.size() ; ++i){
			int l = b[i] - 1 , r = m - b[i]; // 从中间向两边填 
			l = min(l , i + res1) , r = min(r , (int)b.size() - 1 - i + res2);
			ans = max(ans , l + r + 1);
		}
		cout << min(ans , m) << '\n';
	}	
}

D

对于 $k = 1$ , 只能是特殊点自己 , 期望就是 $1$
对于 $k = 2$ , 发现好点只能在两点所在的链上
对于 $k = 3$ , 先确定任意两点的链 , 发现从剩余那个点到这条链的路径上 , 靠近路径一步 , 那么靠经两个点一步 , 远离剩余点一步 , 那么 $ ans = ans - 2 + 1 = ans - 1 $ , 答案会变小 , 那么最优点就是来的路径和链的交点 (再试试在链上走发现远离剩余点，但两点距离不变，答案更差了) , 那么期望也是 $1$

那么对于第二种情况 , 只有一个点在链上它就会产生 $1$ 的贡献 , 那么考虑任选两个点形成的链经过它的概率就好了

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 2e5+5 , M = N * 2;
const ll mod = 1e9+7 , inv2 = 500000004;

int n,k;
int head[N],ver[M],nxt[M],tot;
ll sz[N],p,f[N];

void add(int x,int y)
{
	ver[++tot] = y , nxt[tot] = head[x] , head[x] = tot;	
}

ll ksm(ll a, ll b , ll mod){
	ll base = a % mod , ans = 1;
	while(b){
		if(b & 1) ans = ans * base % mod;
		base = base * base % mod;
		b>>=1;
	}
	return ans;
}
void dfs(int x,int fa)
{
	sz[x] = 1;
	for(int k = head[x] ; k ; k = nxt[k])
	{
		int y = ver[k];
		if(y == fa) continue;
		dfs(y , x);
		sz[x] += sz[y];	
	}
	
	ll pre_sum = 0;
	for(int k = head[x] ; k ; k = nxt[k])
	{
		int y = ver[k];
		if(y == fa) continue;
		//此时枚举的链 , x 一定不为头或者尾 
		f[x] += (n - sz[x]) * sz[y] % mod , f[x] %= mod; // 子与祖先 
		if(pre_sum == 0) pre_sum = sz[y];
		else {
			f[x] += pre_sum * sz[y] % mod , f[x] %= mod;
			pre_sum += sz[y] , pre_sum %= mod;
			//子与子之间 
			// presum 的作用 , 类似于树上背包,保留之前出现过的兄弟的个数  
		}
	}
	f[x] += (n - 1) , f[x] %= mod;  //链以 x 为头或者尾 
}
int main()
{
	scanf("%d %d",&n,&k);
	for(int i = 1 ; i < n ; ++i){
		int x,y;
		scanf("%d %d",&x,&y);
		add(x , y) , add(y , x);
	}
	
	if(k & 1){
		cout << "1\n";
		return 0;	
	}
	
	ll p = 1ll * n * (n - 1) % mod * inv2 % mod; //这里 wa 了一次 , 少了 1ll
	p = ksm(p , mod - 2 , mod); // 1 / C(n , 2);
	
	dfs(1 , 0);
	
	ll ans = 0;
	for(int i = 1 ; i <= n ; ++i)
		ans += f[i] , ans %= mod;

	cout << ans * p % mod << '\n';
}

E

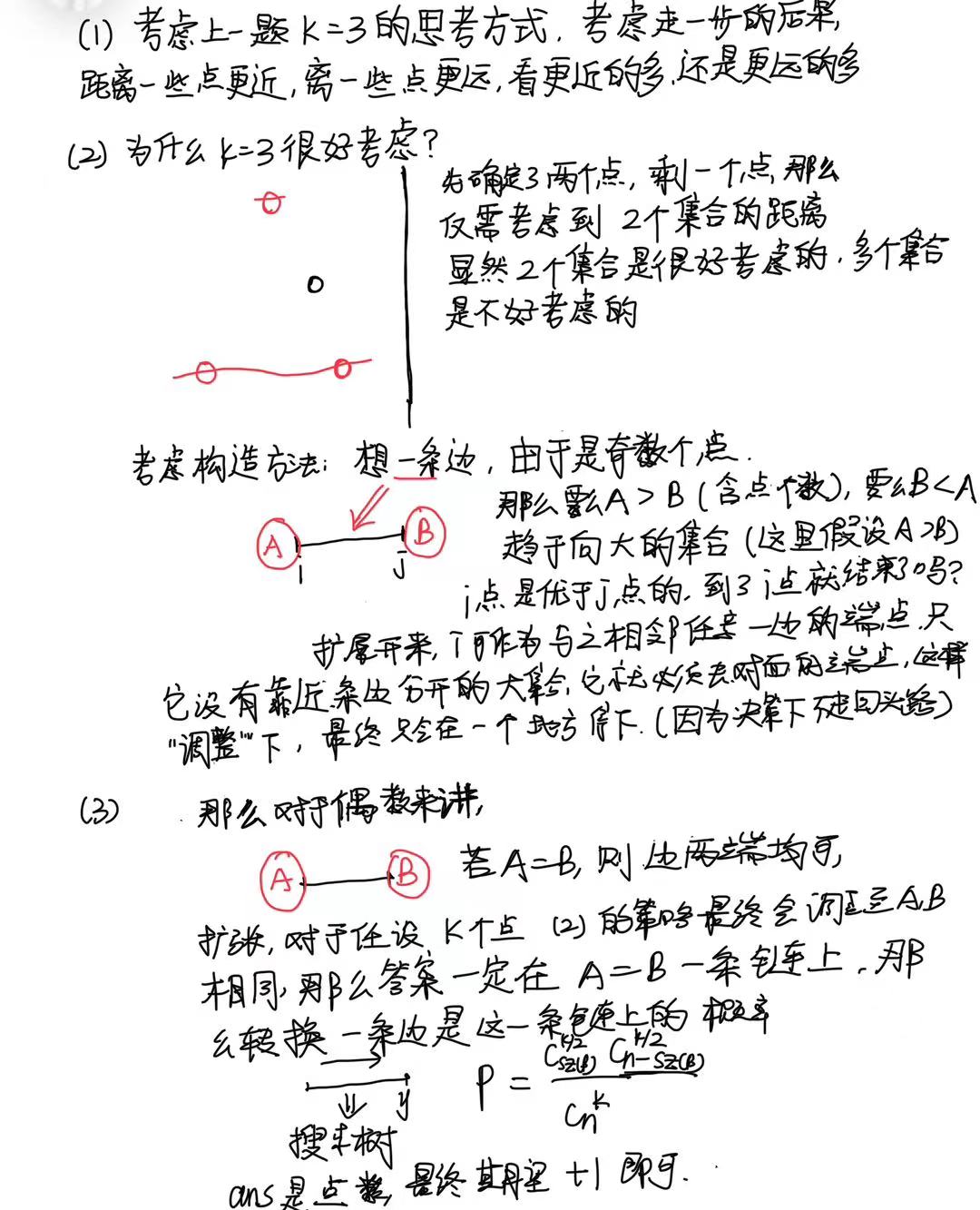
$D$ 的增强版本 , 此时 $k$ 为任意数

大胆猜测 , $D$ 中的 $1,3$ 答案均是 $1$ , 那么是不是 $k$ 为奇数的话 , 答案均为 $1$

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 1e9+7;
const int N = 2e5+5 , M = N * 2;
 
ll n,k;
int head[N],ver[M],nxt[M],tot;
ll sz[N],jc[N];

void add(int x,int y)
{
	ver[++tot] = y , nxt[tot] = head[x] , head[x] = tot;
}
ll ksm(ll a , ll b , ll mod)
{
	a %= mod;
	ll ans = 1;
	while(b){
		if(b & 1) ans = ans * a % mod;
		a = a * a % mod;
		b >>= 1; 
	}
	return ans;
}
ll C(ll n , ll m)
{
	if(m > n) return 0;
	ll up = jc[n] , down = jc[m] * jc[n - m] % mod;
	down = ksm(down , mod - 2 , mod);
	return up * down % mod;
}
void dfs(int x,int fa,ll &ans)
{
	sz[x] = 1;
	for(int i = head[x] ; i ; i = nxt[i])
	{
		int y = ver[i];
		if(y == fa) continue;
		dfs(y , x , ans);
		sz[x] += sz[y];
		ans += C(n - sz[y] , k / 2) * C(sz[y] , k / 2) % mod , ans %= mod;
	}
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0) ; cout.tie(0);
	cin >> n >> k;
	for(int i = 1 ; i < n ; ++i){
		int x,y;
		cin >> x >> y;
		add(x , y) , add(y , x);
	}
	
	if(k & 1) {
		cout << "1\n";
		return 0; 
	}
	
	jc[0] = 1;
	for(int i = 1 ; i <= n ; ++i)
		jc[i] = jc[i - 1] * i % mod;
		
	ll ans = 0;
	dfs(1 , 0 , ans);
	
	ll p = C(n , k);	
	p  = ksm(p , mod - 2 , mod);
	ans = ans * p % mod;
	
	cout << (ans + 1) % mod << '\n';
	return 0;
}

posted @ 2023-05-10 23:23 xqy2003 阅读(19) 评论(0) 收藏举报

刷新页面返回顶部

xqy2003

CF872 Div2

A

B

C

D

E

公告