浅谈树状数组

之前一直没有理解树状数组,学习dalao的 博客 后,顿悟了.

---

原理理解 lowbit(n) = n&(-n)

其中 \(-n\) 的二进制为 \(n\) 的二进制取反加 \(1\).

\(①\) \(:\) 当 \(n\) 为 \(0\) 时 , 结果为 \(0\).

\(②\) \(:\) 当 \(n\) 为 奇数时 ,二进制下最后一位一定是 \(1\) , \(-n\)的二进制取反加 \(1\) 后最后一位一定为 \(1\) ,且没有进位的情况,所以最后的结果为 \(1\) .

\(③\) \(:\) 当 \(n\) 为偶数且为 \(2^n\) 时 , 其二进制有且仅有在 \(n+1\) 位上有一个 \(1\) ,取反后 \(1\) 到 \(n\) 位均为 \(1\) ,再加 \(1\) 进位,又变成了有且仅有在 \(n+1\) 位上有一个 \(1\) ,两者按位与之后还是 \(n\) .

\(④\) \(:\) 当 \(n\) 为偶数且为 \(y \times 2^n\) ,其中 \(y\) 为奇数 . 那么这相当于将 \(y\) 的二进制位左移 \(n\) 位 ,而且由于 \(y\) 是奇数,那么 \(y\) 的最后一位现在的 \(n+1\) 位是 \(1\) .那么取反之后, \(1\) 到 \(n\) 位全为 \(1\) , \(n+1\) 位为 \(0\) , 加 \(1\) 进位以后 \(n+1\) 为 1 ,二者按位与之后就为 \(2^n\).

以上就是lowbit的全部情况 ,至于为什么树状数组能利用lowbit,构建如此不冲突的结构至今没想懂.

加速体现 : \(③\)一次加(减) \(n\) , \(④\) 一次加(减) \(2^n\) .

附上图:

---

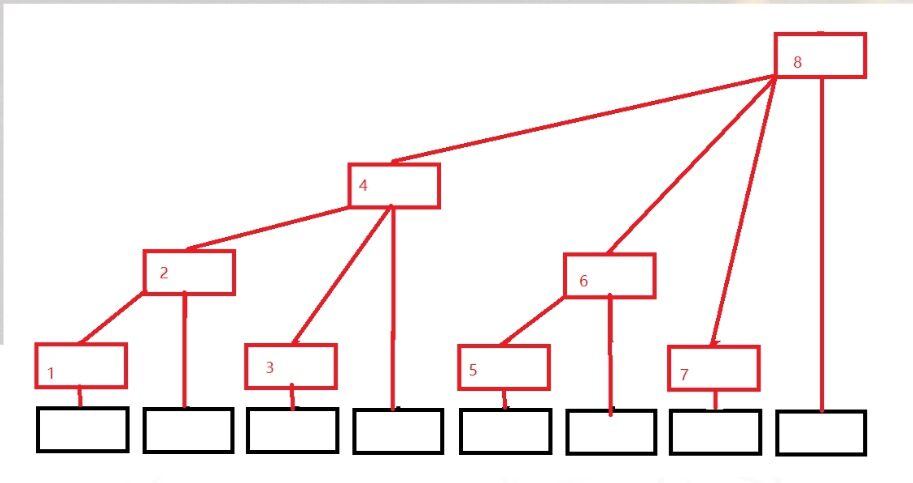
几大功能

\(①\) 单点修改 , 区间查询

理解树状数组结构后就很简单了,修改\(x\) ,对之后加 lowbit 加到 \(n\) 沿途 的数组都要有影响.查询时因为每个数组管理的区间大小不一样,我们直接 lowbit 减到 \(1\) ,加上沿途所有数组的值 , 就得了原数组 \([1,n]\) 的和,在利用前缀和的思想,求出给定区间的值.

//洛谷P3374
#include<iostream>
#include<cstdio>
using namespace std;
#define M 500010
int n,m,a[M],tree[M];
int lowbit(int x) {return x&(-x);}
void add(int x,int val){
	while(x<=n){
		tree[x] += val;
		x += lowbit(x);
	}
}
int getsum(int x){
	int ans = 0;
	while(x){
		ans += tree[x];
		x -= lowbit(x);
	}
	return ans;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
		add(i,a[i]);
	}
	for(int i=1;i<=m;++i){
		int id,x,y;
		scanf("%d%d%d",&id,&x,&y);
		if(id == 1) add(x,y);//x位加上y.
		else cout<<(getsum(y)-getsum(x-1))<<endl;
	}
	return 0;
}

\(②\) \(:\) 区间修改 , 单点查询

利用差分的思想就够了，区间修改就是修改首尾 , 树状数组 \(n\) 前缀和就是原数组第 \(n\) 项的值, 整体维护差分数组.

#include<iostream>
#include<cstdio>
using namespace std;
#define M 500010
int n,m,a[M],tree[M];
int lowbit(int x) {return x&(-x);}
void add(int x,int val){
	while(x<=n){
		tree[x] += val;
		x += lowbit(x);
	}
}
long long getsum(int x){
	long long ans = 0;
	while(x){
		ans += tree[x];
		x -= lowbit(x);
	}
	return ans;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		scanf("%d",&a[i]);
	for(int i=1;i<=n;++i)
		add(i,a[i]-a[i-1]);
	for(int i=1;i<=m;++i){
		int id;
		scanf("%d",&id);
		if(id == 1){
			int x,y,k;scanf("%d%d%d",&x,&y,&k);
			add(x,k),add(y+1,-k);
		}
		if(id == 2){
			int x;scanf("%d",&x);
			cout<<getsum(x)<<endl;
		}
	}
	return 0;
}

\(③\) \(:\) 区间修改 , 区间查询.

区间修改没变,依旧利用差分思想.

区间查询( \(c\) 数组是差分数组)：\(\displaystyle\sum_{i=1}^n\) \(a_i\) = \(c_1\) + ( \(c_1 + c_2\) ) \(+\) ( \(c_1 + c_2 + c_3\) ) . . . . . . = \(c_1\) \(\times\) \(n\) + \(c_2\) \(\times\) \((n-1)\) + ...... = \(n\) \(\times\) (\(c_1 + c_2 + c_3 + ......\)) \(-\) ( \(c_1 \times 0 + c_2 \times 1 + ......\)) = \(n\) \(\times\) \(\displaystyle\sum_{i=1}^n\) \(c_i\) \(-\) \(\displaystyle\sum_{i=1}^n\) \((i-1)\) \(\times\) \(c_i\) ，显然利用树状数组的性质,我们去维护 \(c_i\) 与 \((i-1) \times c_i\) 即可.

#include<iostream>
#include<cstdio>
using namespace std;
#define M 500010
int x,y,k,n,a[M],t1[M],t2[M];
int lowbit(int x) {return x&(-x);}
void add(int x,int val){
	int k = x;
	while(x<=n){
		t1[x] += val;
		t2[x] += val*k;
		x += lowbit(x);
	}
}
int getsum(int x){
	long long ans = 0;
	int k = x;
	while(x){
		ans += k*t1[x] - t2[x];
		x -= lowbit(x); 
	}
	return x;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		scanf("%d",&a[i]);
		add(i,a[i]-a[i-1]); 
	}
	//[x,y]区间加上k.
	add(x,k),add(y+1,k);
	//求[x,y]区间的值.
	cout<<(getsum(y)-getsum(x-1));
	return 0;
}