slope trick

我真的什么也不会。

slope trick 是一种技巧，可以用来维护这样的函数：是凸函数且斜率为整数。

引入

不妨以一道题作为引入：CF13C:

给定序列 \(a_1\cdots a_n\)，求出非降序列 \(b_1\cdots b_n\)，并最小化 \(\sum|a_i-b_i|\)。

显然地，设一个 dp：\(f_{i,j}\) 表示考虑了 \(a_1\) 到 \(a_i\)，\(b_i=j\) 的最小代价，有朴素转移：

\(f_{i,j}=\min\limits_{k\le j}f_{i-1,k}+|a_i-j|\)。

我们现在要证明 \(f_i\) 为凸的。考虑若凸性对于 \(f_{i-1}\) 成立（显然 \(f_1=|a_1|\)，是凸的），我们的转移实际上是做了这样一件事：

把 \(f_{i-1}\) 斜率大于 \(0\) 的一段推平，这相当于取前缀最小值，显然这一步后函数仍具有凸性。

给 \(f_{i-1}\) 加上 \(|a_i-j|\) 以得到 \(f_i\)，凸性函数相加为凸性函数。

故 \(f_i\) 关于 \(j\) 是有凸性的。

凸函数的表示

进行一个曲的差：如何表示一个凸性函数？以下凸壳为一个例子：

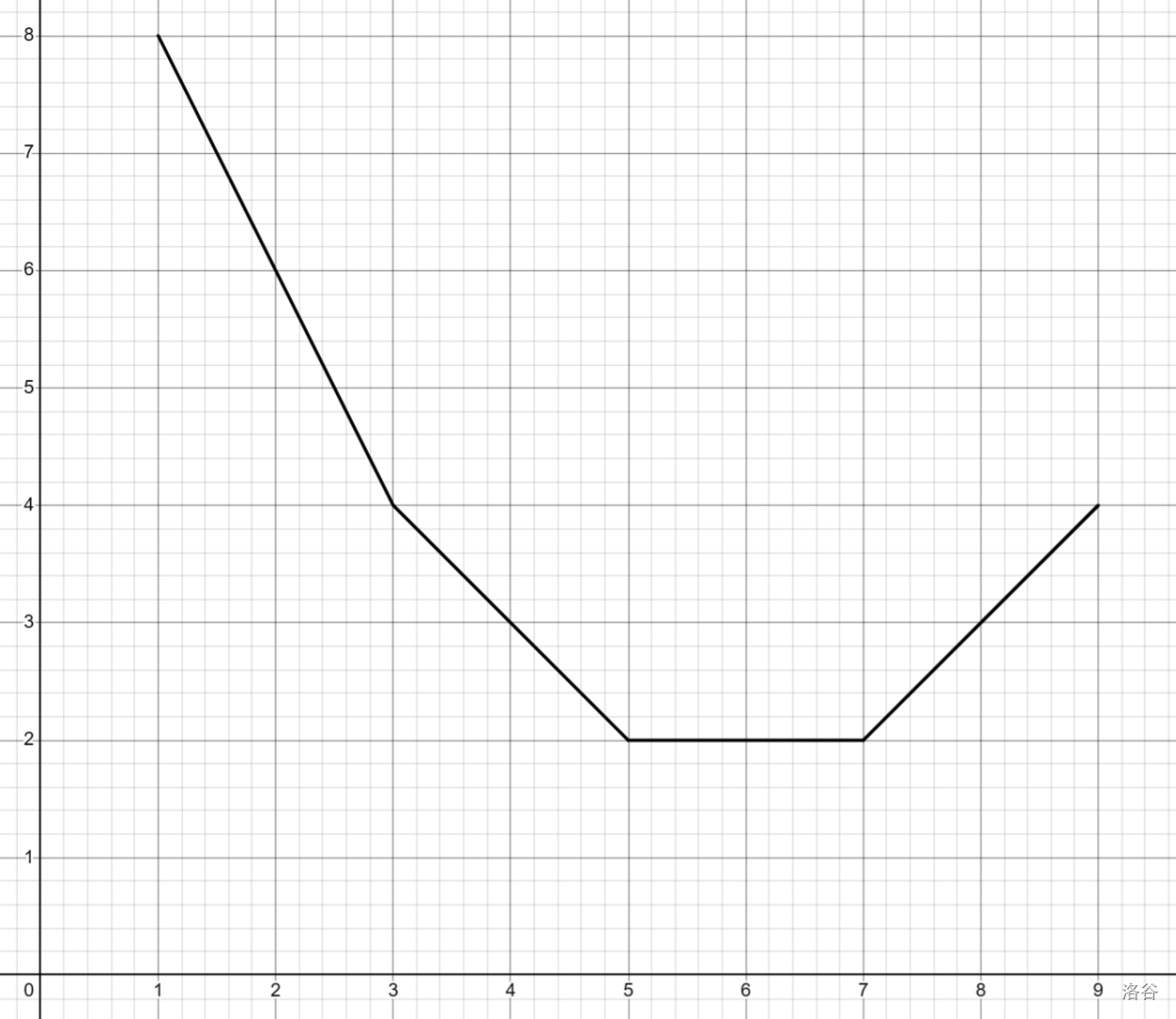
函数的四段斜率分别为 \(-2,-1,0,1\)，斜率最大的部分的函数是 \(y=x-5(x\le9)\)。

维护一个拐点的可重集合，如果函数在 \(x\) 处斜率变化了 \(d\)，我们在集合中插入 \(d\) 个 \(x\)，如图函数的集合是 \(\{3,5,7\}\)，用斜率最大的线段 \(y=x-5(x\le9)\) 与 \(\{3,5,7\}\) 来表示该凸壳。意思是凸壳斜率最大的部分是 \(y=x-5(x\le9)\)，从右到左，在 \(x=\{3,5,7\}\) 处斜率减少了 \(1\)。

当然，如果最左边的线段斜率变成了 \(-3\)，集合会变成 \(\{3,3,5,7\}\)，表示 \(x=3\) 处斜率减少了 \(2\)。

显然这种方式就可以唯一确定一个凸函数，若两凸函数相加，最终结果呈现为斜率最大的线段相加，两者的拐点集合取并。

关于解题

继续思考以上的这道题。我们要求的实际上是 \(f_n\) 中，使得斜率变得等于 \(0\) 的拐点的函数值。

需要发现性质：每次转移时先将函数的后半部分推平，最大斜率为 \(0\)，在此基础上加入绝对值函数，最大斜率变为 \(1\)，就是说删掉拐点集合最大的一个数就可以得到最后是水平的函数。

考虑维护出了 \(f_{i-1}\) 后半部分推平后的函数，斜率最大的函数是 \(y=y_0\)，那么对于前 \(i-1\) 个数，答案就是 \(y_0\)。维护这个 \(res=y_0\)。显然这个问题里，斜率已知，可以只靠维护 \(res\) 来得到最右面的线段。

不妨模拟转移：第一步为加上函数 \(|a_i-x|\)。其最右的部分是 \(y=x-a_i\)，拐点集合是 \(\{a_i,a_i\}\)，设 \(f_{i-1}\) 最大的拐点是 \(s\)。如果看不懂请画个图。

1.若 \(s\le a_i\)，相当于在原函数最后水平的部分大于 \(a_i\) 的斜率加一，整个函数小于 \(a_i\) 部分斜率减一，最小值应当是 \(x=a_i\) 处取得，此时 \(res\) 不变，在集合中插入两个 \(a_i\) 即可。

2.若 \(a_i\le s\)，显然此时 \(res\) 会发生变化。小于 \(a_i\) 的部分斜率减一，没有成为新最小值的可能。\(a_i\) 右面的只有大于 \(s\) 的部分斜率取正，故最小值会在 \(x=s\) 处取得，给 \(res\) 加上 \(s-a_i\) 即可。

3.插入两个 \(a_i\)。

4.推平函数斜率大于 \(0\) 的部分，不难发现这就是弹出集合中的最大值（此时函数斜率最大为 \(1\)）。

用堆维护那个集合，很容易就能写出代码。

#include<iostream>
#include<queue>
int n, rs, x; std::priority_queue<int> q;
int main(){
    std::cin >> n; while(n--)
        std::cin >> x, q.push(x),
        q.push(x), rs += q.top() - x, q.pop();
    std::cout << rs;
}

真的很好用啊。

做题笔记：

CF13C 的经验：P2893 CF713C P4597 P4331(比较恐怖)。

哎呀，要去睡觉了，明天再写。