SNOI 2024 D1T1 题解

唉，这题。唯一一道想出正解还没写出来，果然还是我太菜了。把我赛时的思路写下来。

题意

给你一颗树。对于长为 \(k\) 的序列 \(a\)，元素是树上的点。定义 \(f_x\) 为距 \(x\) 最近的在 \(a\) 中的点在 \(a\) 中的下标，如果有多个距离相同的点取下标更小的。已知树形和 \(f_{1\cdots n}\)，求出合法的 \(a\) 序列数。

\(1\le n,k\le 3000,1\le f_i\le k\)

分析

首先，特殊点本身的 \(f\) 值一定是自己，所以如果 \(1\) 到 \(k\) 中有遗漏一定不能构造。

其次，所有 \(f\) 值相同的点一定在一个连通块里，否则不能构造。这是显然的，可以在搜下去的时候特判一下。

有一个需要你挖掘出来的很重要的性质。对于树上一条连接 \(x,y\) 的边，如果 \(f_x\ne f_y\) 一定意味着在合法方案中，\(x\) 到 \(a_{f_x}\) 的距离和 \(y\) 到 \(a_{f_y}\) 的距离，要么相等，要么差一（是大是小要看 \(a_x\) 和 \(a_y\) 的大小）

证明：定义 \(dis_{x,y}\) 为树上 \(x,y\) 两点的距离。如果我们保证 \(dis_{x,a_{f_x}}=dis_{y,a_{f_y}}\)，一定有 \(dis_{y,a_{f_x}}>dis_{y,a_{f_y}}\)，对于 \(x\) 同理。如果我们让 \(dis_{x,a_{f_x}}=dis_{y,a_{f_y}}+1\) 且有 \(f_x<f_y\)，显然对于 \(y\) 仍然合法，对于 \(x\) 有 \(dis_{x,a_{f_x}}=dis_{x,a_{f_y}}\) 这时有 \(f_x<f_y\) 显然成立。

对于 \(x,y\) 所在连通块里其他的点，以 \(x\) 举例，设这个点是 \(p\)，在 \(p\) 向着远离 \(x\) 的方向移动时，有 \(dis_{p,a_{f_x}}\) 要么减一，要么加一，\(dis_{p,a_{f_y}}\) 一定加一，依然满足限制。所以原性质成立。

不妨来想链的部分分，有以上性质我们来设一个 dp，\(dp_p\) 是满足了 \(1\) 到 \(p\) 所在颜色块的所有限制，且 \(p\) 是关键点（即在 \(a\) 序列中）的方案数。

若 \(p\) 在颜色块的上一个范围是 \([l,r]\)，颜色是 \(k\)，与 \(k\) 交界的颜色与 \(p\) 相同的点是 \(x\)。将 \(dp_{l\cdots r}\) 反转（因为我们的转移和距离有关），得到 \(g_{0\cdots r-l}\)。有转移：

\[f_x=\begin{cases}g_{dis_{x,p}}+g_{dis_{x,p}+1}\qquad a_x>k\\g_{dis_{x,p}}+g_{dis_{x,p}-1}\qquad a_x<k\end{cases} \]

初始时 \(1\) 所在颜色块全设 \(1\)，转移时出现越界的全设成 \(0\) 就行。

soltion

仿照链我们来想树，同样的我们设 \(dp_p\) 为满足根到 \(p\) 的颜色块的限制，\(p\) 是关键点的方案计数，将 \(g_i\) 设成距离 \(x\) 为 \(i+1\) 的所有颜色是 \(k\) 的点的 \(dp\) 值之和。然后仿照转移。答案是所有叶子所在颜色块 \(dp\) 值和的积。

看起来挺对的，但是 \(\text{WA on sample 3}\)。

再想想就发现很假啊，\(dp_p\) 的转移方式很独立，你不能保证这么一个 \(p\) 对应了所有其他的 \(dp\) 值。例如两个颜色块挂在一个相同的块下面，有 \(dp_x=g_1+g_2\) 和 \(dp_y=g_2+g_3\) 这两个显然不能乘，因为它们对应的限制不同。

虽然但是这不挺显然的吗，但是我赛时就是脑子一抽抽没想到，到了最后四十分钟才注意到。

因此我们转移 dp 方式，改成一般的树形 dp，即从儿子们向父亲转移，统计跟所在连通块的答案。这样就对了，且全都合法，考虑原因。

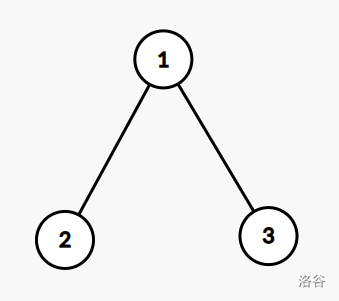
这样的转移方式，我们满足了 \(1\) 与 \(2\)，\(1\) 与 \(3\) 的限制，这时候显然 \(2\) 跟 \(3\) 就不会冲突了。

复杂度最劣 \(O(n^2)\)，dfs 下去 \(O(n)\)，对每一个不同的颜色块我们都要统计一编 \(g\) 的值，这部分也是 \(O(n)\)。不过大概率跑不满。

upd：代码有了。

#include<iostream>
#include<vector>
#define pb push_back
const int p = 998244353, N = 1e7 + 5;
int n, fl, k, rs, a[N], f[N], ct[N];
std::vector <int> e[N], o[N];
inline void gr(std::vector<int> &vc, int x, int fa, int d){
    (vc[d] += f[x]) %= p; for(auto v:e[x]) 
        if(v != fa && a[v] == a[x]) gr(vc, v, x, d + 1);
}
inline void dp(std::vector<int> &vc, int x, int fa, int k, int d){
    f[x] = 1ll * f[x] * (vc[d] + vc[d + (a[x] < k ? -1 : 1)]) % p;
    for(auto v:e[x]) if(v != fa && a[v] == a[x]) dp(vc, v, x, k, d + 1);
}
inline void dfs(int x, int fa){
    ct[a[x]] += a[x] != a[fa];
    if(ct[a[x]] >= 2) return void(fl = 1);
    for(auto v:e[x]) if(v != fa){
        dfs(v, x); if(a[v] != a[x]){
            std::vector<int>vc(n);
            gr(vc, v, x, 1); dp(vc, x, v, a[v], 1);
        }
    }
}
int main(){
    // freopen("in", "r", stdin);
    // freopen("out", "w", stdout);
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    int T; std::cin >> T; while(T--){
        std::cin >> n >> k; rs = fl = 0;
        for(int i = 1; i <= n; i++)
            e[i].clear(), o[i].clear(), ct[i] = 0;
        for(int i = 1, x, y; i < n; i++)
            std::cin >> x >> y, e[x].pb(y), e[y].pb(x);
        for(int i = 1; i <= n; i++) 
            std::cin >> a[i], o[a[i]].pb(i);
        for(int i = 1; i <= n; i++) f[i] = 1;
        dfs(1, 0); for(int i = 1; i <= k; i++)
            if(!ct[i]) {fl = 1; break;}
        if(fl){std::cout << 0 << '\n'; continue;}
        for(auto v:o[a[1]]) (rs += f[v]) %= p;
        std::cout << rs << '\n';
    }
}