P1263

三倍经验紫题，你真的不来做吗？
1263 2825 6062

题意差不多都是这样的：一个网格图，有的地方是墙；有的地方是空地，可以放哨兵（或其他的）；有的地方是陷阱，不可以放哨兵。一个哨兵可以看到他所在的行和列（看不穿墙）。要求哨兵之间不可相互看到，求最多放多少个哨兵？

首先显然地，所有空地一定被看到，因为如果有空地没被看到就可以再放一个哨兵，这也是为什么这道题的结论到 P6062 也是正确的。

考虑连续的一横段或一竖段最多只有一个人，这是经典的二分图匹配模型。陷阱不放人，空地对应的行向列连一条边，然后跑二分图匹配。

现在考虑墙的限制。一道横的墙会把上面的一段和下面的一段隔开，上面的列和下面的列就互不影响了。怎么办呢，以这道墙的边的编号为新的列，如图：

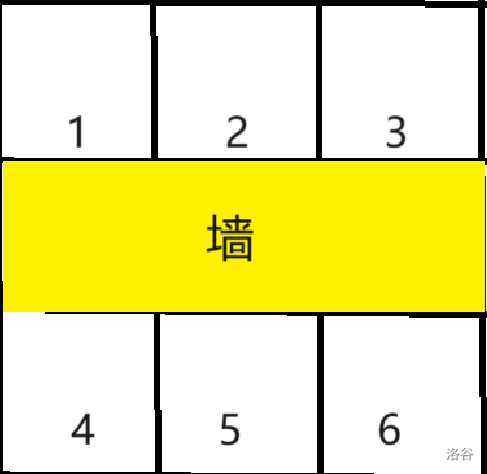
连边时，连新的编号就行了，这样可以处理墙的限制，列也是同理的

代码实现上，如果有一道墙，他的上面应当被作为列的编号，对应的是墙上面所有可达的空地。右面省略。另外，为处理不被墙限制的点，在地图的外围围一堵墙。由于 \(n\) 只有区区 \(200\)，可以让点 \((i,j)\) 的下方和右方的线标号为 \((i-1)\times200+j\) 和 \((i-1)\times200+j+40000\) 这样可以不重叠，然后跑一遍二分图，最后最大流就是结果。

另外要构造出一组可行解，由行连向列的正向边如果有流通过，对应的点是答案。

我在代码里用了 \(dinic\)，由于有 \(n^2\) 个点，复杂度是 \(n^2\times \sqrt {n^2}=O(n^3)\) 的。

#include<bits/stdc++.h>
using namespace std; int wl[202][202][2], now[80002];
int n, m, s, t, mp[202][202], dep[80002], res; const int inf = 1e9;
struct edge{int u, v, w, nxt;}e[1000010]; int cnt = 1, head[80002];
inline void add(int u, int v){
    e[++cnt] = (edge){u, v, 1, head[u]}; head[u] = cnt;
    e[++cnt] = (edge){v, u, 0, head[v]}; head[v] = cnt;
} // 加边
inline bool bfs(){
    memset(dep, -1, sizeof dep);
    queue<int>q;
    q.emplace(s); dep[s] = 0;
    while(q.size()){ int x = q.front(); q.pop();
        for(int i = head[x]; i; i = e[i].nxt){ auto o = e[i]; int v = o.v;
            if(o.w && dep[v] == -1) dep[v] = dep[x] + 1, q.emplace(v);}
    } for(int i = 0; i <= 80001; i++) now[i] = head[i]; return dep[t] != -1;
}
inline int dfs(int x, int lim){
    if(x == t) return lim; int used = 0;
    for(int &i = now[x]; i; i = e[i].nxt){ 
        auto o = e[i]; int v = o.v;
        if(dep[v] == dep[x] + 1 && o.w){
            int t = dfs(v, min(lim, o.w));
            used += t; e[i].w -= t; e[i^1].w += t;
            if (t == lim){now[x] = i; break;}
        }
    }
    if (!used){dep[x] = -1;}
    return used;
}//网络流部分
int main(){
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);std::cout.tie(0);
    cin >> n >> m; s = 0, t = 80001;
    for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++) cin >> mp[i][j];
    for(int i = 0; i <= n + 1; i++) mp[i][0] = 2, mp[i][m + 1] = 2; 
	for(int i = 1; i <= m + 1; i++) mp[0][i] = 2, mp[n + 1][i] = 2; //先围一堵墙
    for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)
		if(mp[i][j] != 2){
			int ps = (i - 1) * 200 + j;
			if(mp[i + 1][j] == 2){
                add(s, ps); for(int k = i; mp[k][j] != 2; k--) wl[k][j][0] = ps;
			}if(mp[i][j + 1] == 2){ ps += 40000;
                add(ps, t); for(int k = j; mp[i][k] != 2; k--) wl[i][k][1] = ps;
			} //这部分是求出每个点对应的行和列（新的）
		} int ct = cnt + 1;
	for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++)
		if(!mp[i][j]) add(wl[i][j][0], wl[i][j][1]); //二分图的连边
    while(bfs()) res += dfs(s, inf); //跑最大流
    cout << res << '\n';
    for(int i = ct; i <= cnt; i++) if(!e[i].w && (e[i].v >= 40001))
        cout << (e[i].v - 40001) / 200 + 1 << ' ' << (e[i].u - 1) % 200 + 1 << '\n'; //构造方案。
    return 0;
}