零基础入门数据分析三大核心算法：线性回归、逻辑回归、决策树

作为数据分析新手，入门时最绕不开的就是线性回归、逻辑回归、决策树这三个基础算法。它们不仅是后续学习复杂模型（如随机森林、神经网络）的基石，还能解决 80% 的日常数据分析场景（比如预测房价、判断用户是否流失、分类商品类型）。
一、先搞懂：三个算法分别解决什么问题？
在学算法前，先明确核心目标 —— 不同算法对应不同的「预测需求」，用一张表说清：

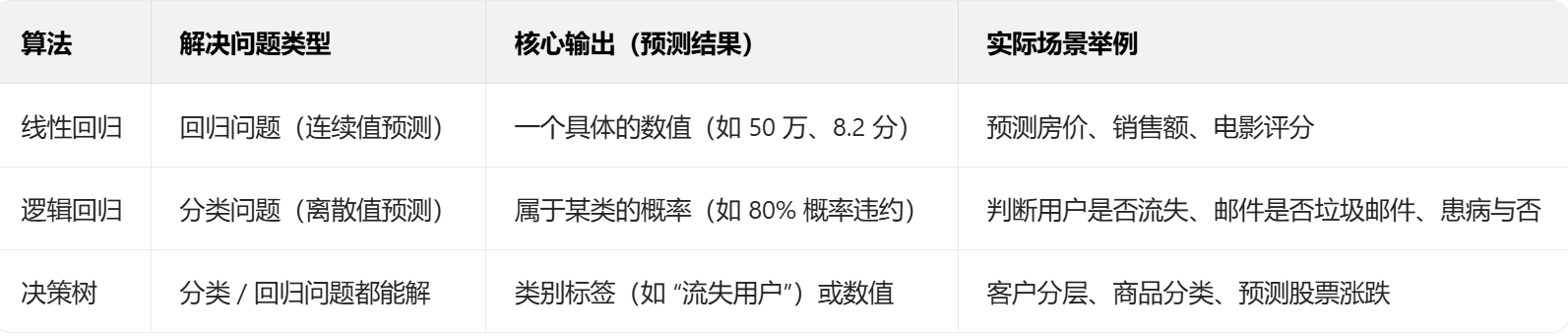
简单来说：
想预测「具体数值」→ 用线性回归；
想判断「是 / 否、A/B/C 类」→ 优先选逻辑回归（二分类）或决策树（多分类 / 回归）；
想让模型结果「一眼看懂」→ 决策树（像流程图一样直观）。

二、逐个拆解：从思想到代码落地
（一）线性回归：预测 “具体数值” 的 “直线拟合术”
1. 场景引入
假设你是房产中介，想通过「房屋面积」预测「房价」。收集了 100 套房子的数据（面积：50㎡→150㎡，房价：30 万→120 万），把数据画成散点图，会发现：面积越大，房价越高，且大致呈 “直线趋势”。

线性回归的核心就是：找到一条 “最贴合” 这些散点的直线，用这条直线来预测新房子的房价。

2. 核心思想
用「直线方程」描述特征（如面积）和目标（如房价）的关系，然后通过数据 “校准” 直线的参数，让直线尽可能靠近所有数据点。

3. 数学原理
我们小学学过的直线方程是：y = kx + b（k 是斜率，b 是截距）。

在线性回归中，这个方程升级为：y = w₁x₁ + w₂x₂ + ... + wₙxₙ + b

• y：要预测的目标（如房价）；
• x₁、x₂...xₙ：影响目标的特征（如面积、房间数、楼层，n 是特征个数）；
• w₁、w₂...wₙ：每个特征的 “权重”（表示这个特征对目标的影响大小，比如面积的权重比楼层大）；
• b：截距（可以理解为 “基础值”，比如即使面积为 0，理论上的基础房价，实际中可忽略物理意义）。

核心目标：找到一组w和b，让所有数据点的「预测值 y̅」和「真实值 y」的误差最小。

怎么衡量误差？最常用的是「最小二乘法」—— 简单说就是：让所有点到直线的 “距离平方和” 最小（平方是为了避免正负误差抵消）。

4. 代码实现（预测波士顿房价）
用 Python 的sklearn库（数据分析必备），步骤：导入库→加载数据→预处理→划分训练 / 测试集→训练模型→预测→评估。

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston  # 波士顿房价数据集
from sklearn.model_selection import train_test_split  # 划分训练/测试集
from sklearn.linear_model import LinearRegression  # 线性回归模型
from sklearn.preprocessing import StandardScaler  # 特征缩放（可选，提升梯度下降效率）
from sklearn.metrics import r2_score, mean_squared_error  # 模型评估指标

# 2. 加载数据（sklearn自带经典数据集）
boston = load_boston()
# 特征矩阵X（影响房价的因素：面积、房间数等13个特征），目标向量y（房价）
X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.Series(boston.target, name='price')

# 3. 数据预处理（简单处理：特征缩放，线性回归用梯度下降时需要，正规方程不需要）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)  # 缩放后特征均值为0，方差为1

# 4. 划分训练集（70%教模型）和测试集（30%考模型）
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.3, random_state=42  # random_state固定划分方式，方便复现
)

# 5. 初始化并训练模型
lr_model = LinearRegression()  # 初始化模型（默认用正规方程求解w和b）
lr_model.fit(X_train, y_train)  # 用训练集“教”模型

# 6. 预测（用测试集考模型）
y_pred = lr_model.predict(X_test)

# 7. 模型评估（看预测准不准）
mse = mean_squared_error(y_test, y_pred)  # 均方误差（越小越好）
r2 = r2_score(y_test, y_pred)  # R²（越接近1越好，1表示完美预测）

print(f"均方误差（MSE）：{mse:.2f}")
print(f"决定系数（R²）：{r2:.2f}")
print(f"模型参数（w）：{lr_model.coef_[:5]}...")  # 输出前5个特征的权重（共13个）
print(f"截距（b）：{lr_model.intercept_:.2f}")

运行结果解读：

1. R²≈0.71：表示模型能解释 71% 的房价变化，对于基础模型来说算不错；
2. 权重w的正负：正数表示特征与房价正相关（如RM：房间数越多，房价越高），负数表示负相关（如LSTAT：低收入人口比例越高，房价越低）。

5. 优缺点 & 适用场景

（二）逻辑回归：判断 “是 / 否” 的 “概率转换器”
1. 场景引入
假设你是银行风控专员，想通过「用户收入、信用记录、负债情况」判断「用户是否会违约」（结果只有两种：违约 / 不违约）。

这里的核心是「分类」，不是预测具体数值。但线性回归的输出是连续值（比如预测违约概率为 120%，这显然不合理），所以需要一个 “转换器”，把线性回归的输出映射到 0~1 之间 —— 这就是逻辑回归的核心。

2. 核心思想

1. 先用线性回归的方式计算「线性得分」：z = w₁x₁ + w₂x₂ + ... + wₙxₙ + b；
2. 用「sigmoid 函数」把z映射到 0~1 之间，得到「概率值」：p = 1 / (1 + e^(-z))；
3. 设定阈值（默认 0.5）：p≥0.5 → 预测为 “违约”，p<0.5 → 预测为 “不违约”。

3. 数学原理（通俗版）

• sigmoid 函数：形状像 “S”，当 z→+∞时，p→1；z→-∞时，p→0；z=0 时，p=0.5。完美解决 “概率在 0~1 之间” 的问题。
• 核心目标：找到一组w和b，让「所有样本的预测概率尽可能接近真实标签」（比如真实违约的样本，p 尽可能接近 1；真实不违约的，p 尽可能接近 0）。
  这里用「对数似然估计」来衡量（不用深究公式），简单说就是：让 “预测对” 的概率最大化。

4. 代码实现（判断鸢尾花是否为山鸢尾）
用鸢尾花数据集，简化为二分类问题（预测是否为山鸢尾）：

# 1. 导入库
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris  # 鸢尾花数据集
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression  # 逻辑回归模型
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report  # 分类评估指标

# 2. 加载数据并简化为二分类
iris = load_iris()
X = pd.DataFrame(iris.data, columns=iris.feature_names)  # 特征：花萼长度、宽度等4个
y = pd.Series(iris.target, name='species')
# 简化为二分类：只判断是否为山鸢尾（target=0），其他为1
y_binary = (y == 0).astype(int)  # 0=山鸢尾，1=非山鸢尾

# 3. 特征缩放（逻辑回归用梯度下降，必须缩放！）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 4. 划分训练/测试集
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y_binary, test_size=0.3, random_state=42
)

# 5. 训练模型（penalty='l2'是正则化，防止过拟合，新手默认即可）
lr_clf = LogisticRegression(penalty='l2', max_iter=1000, random_state=42)
lr_clf.fit(X_train, y_train)

# 6. 预测（两种预测：概率和类别）
y_pred_prob = lr_clf.predict_proba(X_test)[:, 1]  # 预测为“非山鸢尾”的概率
y_pred = lr_clf.predict(X_test)  # 预测类别（0/1）

# 7. 模型评估
accuracy = accuracy_score(y_test, y_pred)  # 准确率（正确预测的比例）
conf_matrix = confusion_matrix(y_test, y_pred)  # 混淆矩阵（看真阳性、假阳性等）
class_report = classification_report(y_test, y_pred)  # 综合评估（精确率、召回率、F1）

print(f"准确率：{accuracy:.2f}")
print("混淆矩阵：")
print(conf_matrix)
print("分类报告：")
print(class_report)
print(f"特征权重：{lr_clf.coef_[0]}")  # 每个特征对分类的影响（正数=促进非山鸢尾，负数=促进山鸢尾）

运行结果解读：

• 准确率≈1.0：表示测试集中所有样本都预测正确（鸢尾花数据集太简单）；
• 混淆矩阵：[[15, 0], [0, 30]] → 15 个山鸢尾全预测对，30 个非山鸢尾全预测对；
• 特征权重：比如「花萼长度」权重为负 → 花萼越短，越可能是山鸢尾（符合实际特征）。

5. 常见疑问：为什么叫 “回归” 却是分类算法？
因为它的核心框架是「线性回归」（先计算 z=wx+b），只是在输出端加了 sigmoid 函数做 “分类转换”，名字是历史沿用的，本质是二分类算法（也可通过修改参数支持多分类）。

6. 优缺点 & 适用场景

（三）决策树：像 “流程图” 一样的 “分类 / 回归神器”
1. 场景引入
假设你想判断「一个用户是否会购买某商品」，已知用户的「年龄（<25/25-35/>35）、收入（高 / 中 / 低）、是否有会员」。

决策树的核心是「分而治之」：先选一个最能区分 “购买 / 不购买” 的特征（比如年龄），把数据分成几组；再在每组里选下一个特征（比如收入），继续细分；直到所有样本都被分到 “纯度足够高” 的组（比如某组里 90% 的用户都购买了），就停止分裂，输出结果。

最终的模型就像一个「流程图」：

年龄<25？→ 是→ 有会员？→ 是→ 购买；否→ 不购买  
          → 否→ 收入高？→ 是→ 购买；否→ 不购买

2. 核心思想

1. 特征选择：每次分裂时，选择「能让数据 “纯度” 提升最多」的特征（比如年龄比收入更能区分购买行为）；
2. 纯度衡量：

• 分类问题：用「熵」（混乱度，熵越小越纯）或「Gini 系数」（不纯度，Gini 越小越纯）；
  比如：一组全是购买用户（熵 = 0，最纯），一组一半购买一半不购买（熵最大，最混乱）；
• 回归问题：用「均方误差（MSE）」（误差越小越纯）；

3. 停止分裂：当节点样本数太少、纯度达到阈值，或树的深度达到上限时，停止分裂，每个叶子节点的结果就是预测值（分类 = 多数类，回归 = 平均值）。

3. 数学原理

• 熵（Entropy）：衡量数据混乱度，公式：H = -Σp(i)log₂p(i)（p (i) 是第 i 类的比例）；
  例：某节点有 10 个样本，6 个购买（p=0.6），4 个不购买（p=0.4）→ 熵≈0.97（混乱）；
  若 10 个全购买（p=1）→ 熵 = 0（纯净）。
• 信息增益：分裂后熵减少的量（信息增益 = 父节点熵 - 子节点熵的加权和）；
  每次分裂都选「信息增益最大」的特征，因为这意味着分裂后数据更纯。

4. 代码实现（泰坦尼克号生存预测）
用泰坦尼克号数据集，预测乘客是否生存（分类问题）：

# 1. 导入库
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml  # 加载泰坦尼克数据集
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree  # 决策树分类器+可视化
from sklearn.preprocessing import LabelEncoder  # 处理分类特征（如性别、舱位）
from sklearn.metrics import accuracy_score, classification_report
import matplotlib.pyplot as plt

# 2. 加载并预处理数据（泰坦尼克数据集需要处理缺失值和分类特征）
titanic = fetch_openml('titanic', version=1, as_frame=True)
df = titanic.frame

# 简化特征：只保留Pclass（舱位）、Sex（性别）、Age（年龄）、Survived（是否生存）
df = df[['Pclass', 'Sex', 'Age', 'Survived']]

# 处理缺失值：Age用平均值填充
df['Age'].fillna(df['Age'].mean(), inplace=True)

# 处理分类特征：Sex（男/女）转成数值（0/1）
le = LabelEncoder()
df['Sex'] = le.fit_transform(df['Sex'])  # 0=女，1=男

# 拆分特征X和目标y
X = df[['Pclass', 'Sex', 'Age']]
y = df['Survived'].astype(int)  # 转成整数（0=死亡，1=生存）

# 3. 划分训练/测试集
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

# 4. 训练决策树模型（控制树的深度，防止过拟合）
dt_clf = DecisionTreeClassifier(max_depth=3, random_state=42)  # max_depth=3：树最多3层
dt_clf.fit(X_train, y_train)

# 5. 预测和评估
y_pred = dt_clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
class_report = classification_report(y_test, y_pred)

print(f"准确率：{accuracy:.2f}")
print("分类报告：")
print(class_report)

# 6. 可视化决策树（重点！看模型如何决策）
plt.figure(figsize=(12, 8))
plot_tree(dt_clf, feature_names=X.columns, class_names=['死亡', '生存'], filled=True, rounded=True)
plt.title('泰坦尼克号生存预测决策树')
plt.show()

运行结果解读：

• 准确率≈0.82：比逻辑回归在这个数据集上表现更好（因为数据有非线性关系，比如 “女性 + 高舱位” 生存概率高）；
• 可视化图：根节点是「Sex」（性别）→ 说明性别是判断生存的最重要特征（符合历史事实：女性优先获救）；
• 比如：Sex=0（女）→ 再看 Pclass（舱位）→ 1/2 舱位→ 生存，3 舱位→ 再看 Age→ 年龄 < 9.5→ 生存，否则死亡。

5. 优缺点 & 适用场景

6. 如何避免过拟合？
决策树最容易犯的错是「过拟合」（训练集准确率高，测试集准确率低），解决方法：

• 限制树的深度（max_depth）；
• 限制每个节点的最小样本数（min_samples_split）；
• 剪枝（ccp_alpha参数）：去掉不重要的分支。

三、三大算法核心对比（一目了然）

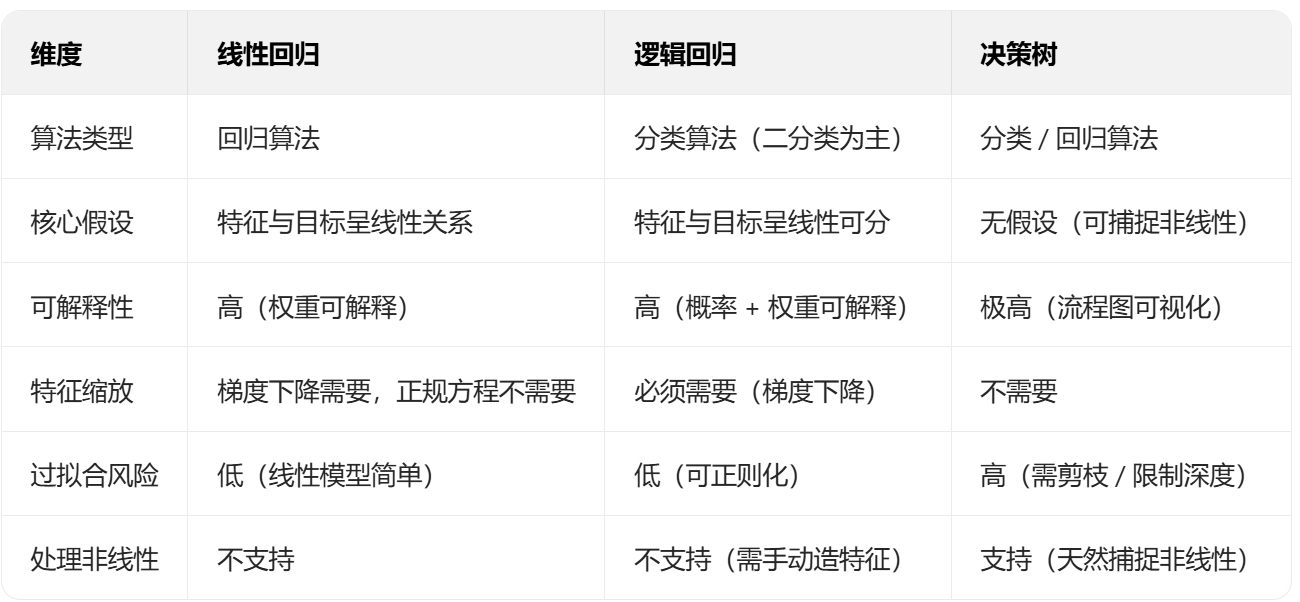
四、新手学习建议

1. 先理解 “解决什么问题”，再看原理：不用死磕公式推导，先搞懂每个算法的适用场景（比如预测数值用线性回归，分类用逻辑回归 / 决策树）；
2. 动手跑代码，修改参数看效果：比如决策树的max_depth从 3 改成 5，看准确率是否下降（过拟合）；逻辑回归的penalty改成l1，看特征权重是否变化；
3. 用可视化辅助理解：线性回归画散点图 + 拟合直线，决策树画流程图，能快速 get 核心；
4. 从简单数据集入手：先玩 sklearn 自带的数据集（波士顿房价、鸢尾花、泰坦尼克），再用自己的数据集实践。

这三个算法是数据分析的 “基本功”，打好基础后，再学习集成学习（如随机森林、XGBoost）就会轻松很多 —— 因为集成学习本质就是 “多个决策树 / 线性模型的组合”。