AES加密算法C语言实现-128CBC
概述
原本想把自己AES加密算法的整个实现过程给详细复述下来,分享给想学习的同学,也方便自己复习,但后来发现该工作量太大,加上作业太多没有过多的时间去写。所以就想把自己在学习的过程中多遇到的好的文章进行汇总,避免重复性的工作,因为我感觉有的文章的介绍和配图写的非常好,再次重复也没有意义。本文里我会将文章的链接附上,如有侵权,敬请告知!
因为最近要完成课程作业,实现AES128加解密,本以为就是一个简单的算法实现,后来发现AES加密的每一步都挺难,而且都涉及到我没听过的概念,所以最近看了很多帖子、资料。最终终于能够解决这个问题。关于AES算法的介绍,网上有很多的帖子,所以我就不进行赘述了,我只是希望将我遇到的一些比较难以理解的点进行详细的叙述。
实现AES算法主要包括以下学习步骤:
- GF(2^8)域上的多项式运算
- 扩展的欧几里德算法
- 生成S盒
- 生成逆S盒
- S盒置换
- 行移位
- 列混合
- 生成秘钥
- 循环加密
其中1、2、3、4步都跟S盒生成有关,根据我所看的一些博客,S盒的生成涉及到数论的基础知识。如果没有基础的话,1、2是要专门去学习的,我在这两步上花费了很多时间。但是在网上也可以找到很多AES算法,他们用的是现成的S盒,没有前4步,直接用现成的S盒置换,这样相对会容易一些。但是本着刨根问底和多学习知识的原则,我还是去学习了S盒的生成方式。第5步就是将每一个字符进行查表替换,没有什么难以理解的地方,所以相对而言比较容易。第6步应该是整个过程当中最简单的一步了,就是进行一个循环移位。第7步列混合涉及到矩阵和多项式的乘法,所以还是有一定难度,。。。
如果想从整体上了解AES加密的完整过程,那么下面几篇文章不管从叙述还是插图上来看都是很不错的,几篇文章介绍的方式不同,但是原理都是一样的,对比结合着看会更有帮助:
https://www.cnblogs.com/block2016/p/5596676.html
https://blog.csdn.net/u012721519/article/details/79612128
https://www.cnblogs.com/luop/p/4334160.html
http://www.alonemonkey.com/2016/05/25/aes-and-des/
但是仅从这几篇文章来看的话,对于像我这样的小白而言还是没有办法实现的,因为各个步骤介绍的并不具体,尤其是对于缺少基本数学知识学习的同学很难理解。所以这几篇文章可以作为整体进度的把控,接下来看怎么一步步学习实现。
S盒
我在学习这个算法的时候,在S盒的生成及置换上花费的时间是最多的。可能是因为基础较差,所以需要学习的东西比较多,所以我将这一部分进行了逐项的划分。关于S盒的生成及置换,这篇博客进行了非常详细的介绍,但是有一些东西我还是没明白,所以又参考了很多其他文章,才把这一部分搞明白。建议初学者以这篇博客为基础进行学习:
https://blog.csdn.net/u011516178/article/details/81221646
下面进行分步的介绍。
GF(2^8)域上的多项式计算
因为整个过程很多,所以我决定分为多个文章分别进行叙述,首先是GF(2^8)域上的多项式计算,因为以前也没有学过相关知识,很多概念都是第一次见到,所以这部分花了很长时间去学习。在学习这个之前,我们需要知道为什么去学习这个东西,AES加密中的哪一步用到了该知识点呢?
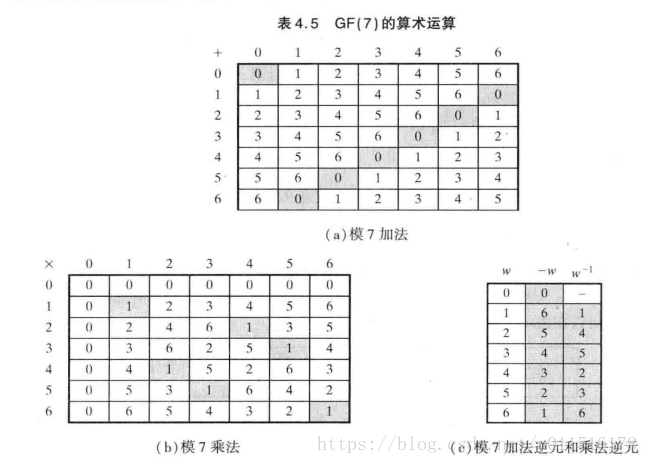
S盒的置换就是将0~2^8中的任意一个字节置换为另外一个,置换的原则是将该元素置换为在GF(2^8)域上的乘法逆元,什么是GF(2^8)域?什么又是逆元呢?这些定义的准确数学描述我不太懂,根据本次应用,我可以给出粗略说明,GF(2^8)有限域大概就是指定义在该域中的数值经过定义在该域上的函数运算,其结果也都在该域内, 借用网上的一个例子进行说明:
那什么又是乘法逆元呢,形如:
其中p为有限域的范围,这里按理说应该为2^8,但是却不能取这个数,因为2^8并不与其内的每一个数互质,所以只能选一个更大的质数(具体原因请参考扩展的欧几里德算法),AES算法中p的值选的是0x11B, 我也不知道为什么,可能是约定俗成的吧,因为如果想找一个稍微比255大的质数,不知道为什么要取283(0x11B)。 为有限域内的整数,那么
即为
在有限域上的逆元。至此,我们知道逆元是什么,但是具体怎么去求解还不太清楚,这一部分请参照扩展的欧几里德算法。(更新)后来为了加深学习,我又自己写了篇博客。
我接下来继续说GF(2^8)域上的多项式运算,因为把基本的运算搞清楚是计算GF(2^8)域上乘法逆元的前提,该域上的加减乘除运算是与传统的运算所不同的,具体的多项式运算请参考GF(2^8)域上的多项式运算。当然,也可以先学习扩展的欧几里德算法,然后再学习该部分,实现的时候将欧几里德算法中的四则运算换成GF(2^8)域上的多项式运算就行了。关于GF(2^8)域的计算介绍参考以下几篇博客介绍:
https://blog.csdn.net/luotuo44/article/details/41645597
https://blog.csdn.net/shelldon/article/details/54729687
http://abcdxyzk.github.io/blog/2018/04/16/isal-erase-3/
在四则运算中,加减运算就是简单的异或运算,很简单。而乘除运算则是以乘法运算为基础,所以四则运算中最主要的是理解乘法的运算,这篇https://blog.csdn.net/bupt073114/article/details/27382533文章详细介绍了乘法运算,以及其实现。
拓展的欧几里得算法
待掌握了GF(2^8)域的运算知识后,应该去学一下拓展的欧几里得算法,对于该算法,上面所给出的关于S盒生成的综述博文里已经参考相关教材进行了非常详细的论述,所以关于这部分知识可以同样参考这篇博文(参考文献10),
还可以参考以下这篇博客:
https://www.cnblogs.com/frog112111/archive/2012/08/19/2646012.html
如果还不明白,也可以自行查找其他关于拓展欧几里得算法的介绍。
S盒生成及置换
关于S盒的生成及置换,同样参考文献10,该文章已经进行了非常详尽的描述与代码实现。待自己完成后也可以参考博客中的结果进行检验。
行移位
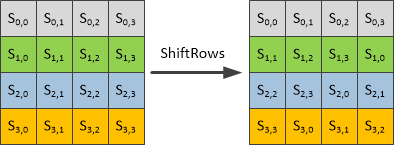
行移位就是对每行数据进行相应的循环移位,没有难以理解的地方,应该是整个加密过程最简单的部分,关于移位的规则,可以参考文献1、2、3、4,均有详细的图示介绍。下图来源于文献4:
列混合
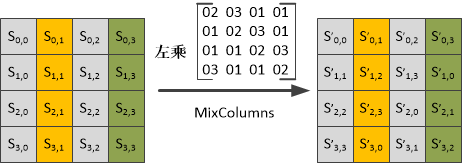
列混合就是将数据矩阵乘上一个矩阵,解密的时候乘上原矩阵的逆矩阵进行解密,秩序要按照步骤一步步来即可,同样没有难以理解的地方,按照参考文献1、2、3、4的介绍进行操作就没有问题。关于列混合还可以参照这篇专门介绍的文章[11],其对于列混合又专门的介绍与实现,而且还有检验数据。下图参照文献4中图片:
密钥生成
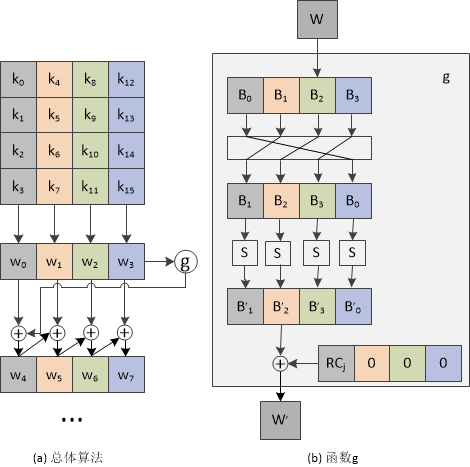
密钥的生成过程稍微有些麻烦,需要仔细参考规则,避免搞错,但是只需要理解操作规则即可,不需要理论理解,还好参考文献3、4中都有非常生动的图示。下图来源于文献4:
循环加密
循环加密就是对上述过程重复进行若干次。具体实现参照文献1、2、3、4。
解密
解密过程就是将上述的过程反过来执行一遍,原本置换的就置换过来;原本移位的就反向移过来;原本乘上矩阵的就乘上她的逆矩阵。。。上面关于每个加密过程的参考文献都有相应的解密过程。
实现
关于AES128的加密完整实现,可以参照代码https://github.com/xinyu-yang/AES128-CBC,此代码的实现几乎都是参照上文的介绍,唯一不同的是在加密的时候采用了CBC模式,具体什么是CBC加密模式,如果不清楚的可以自行百度。如果有时间我也会把这部分补全。
查看更多内容
参考文献:
1、https://blog.csdn.net/zhjchengfeng5/article/details/7786595
2、https://www.cnblogs.com/block2016/p/5596676.html
3、https://blog.csdn.net/u012721519/article/details/79612128
4、https://www.cnblogs.com/luop/p/4334160.html
5、http://www.alonemonkey.com/2016/05/25/aes-and-des/
6、https://blog.csdn.net/luotuo44/article/details/41645597
7、https://blog.csdn.net/shelldon/article/details/54729687
8、http://abcdxyzk.github.io/blog/2018/04/16/isal-erase-3/
9、https://blog.csdn.net/bupt073114/article/details/27382533
10、https://blog.csdn.net/u011516178/article/details/81221646
11、https://blog.csdn.net/u012620515/article/details/49893905
12、https://www.cnblogs.com/frog112111/archive/2012/08/19/2646012.html
13、https://www.cnblogs.com/xinyuyang/p/11439638.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号