Prim算法

普利姆算法，是一种常用的求最小生成树的算法。

最小生成树，使得一个连通图内拥有最小的和。对现实生活中有极大的作用。

主要思路

1 选定一个顶点（与结果无关）

2 寻找与这个顶点相连的最小权值的邻居

while(j<MAXSIZE){  //寻找生成树相连的最小权值的顶点
            if(lowcost[j]!=0  && lowcost[j] < min){
                min = lowcost[j];
                k = j;
            }

            j++;
        }

3 把这个邻居，加入到最小生成树集合中。

4 在此新加入的顶点基础上，寻找与该集合相连的最小权值的邻居。重复2。

for(j=1;j<MAXSIZE;j++){
            if(lowcost[j]!=0 && g->arc[k][j] < lowcost[j]){
                lowcost[j] = g->arc[k][j];
                ver[j] = k;
            }

        }

5 直到所有顶点都存在于该集合中

算法代码

 1 void Prim(Graph *g){
 2     int min,i,j,k;
 3     int ver[MAXSIZE];
 4     int lowcost[MAXSIZE];
 5     lowcost[0] = 0;
 6     ver[0] = 0;
 7     for(i=1;i<MAXSIZE;i++){
 8         lowcost[i] = g->arc[0][i];
 9         ver[i] = 0;
10     }
11     for(i=1;i<MAXSIZE;i++){
12         min = INF;
13 
14         j=1;
15         k=0;
16 
17         while(j<MAXSIZE){  //寻找生成树相连的最小权值的顶点
18             if(lowcost[j]!=0  && lowcost[j] < min){
19                 min = lowcost[j];
20                 k = j;
21             }
22 
23             j++;
24         }
25 
26         printf("(%d , %d)\n",ver[k],k);
27 
28         lowcost[k] = 0;
29 
30         for(j=1;j<MAXSIZE;j++){
31             if(lowcost[j]!=0 && g->arc[k][j] < lowcost[j]){
32                 lowcost[j] = g->arc[k][j];
33                 ver[j] = k;
34             }
35 
36         }
37     }
38 }

示例代码

 1 #include <stdio.h>
 2 #include <stdlib.h>
 3 #define MAXSIZE 9
 4 #define INF 65535
 5 typedef struct Graph{
 6     int arc[MAXSIZE][MAXSIZE];
 7 }Graph;
 8 
 9 void initGraph(Graph *g);
10 void showGraph(Graph *g);
11 void Prim(Graph *g);
12 
13 int num[MAXSIZE][MAXSIZE]={ 0,  10, INF,INF,INF,11, INF,INF,INF,
14                 10, 0,  18, INF,INF,INF,16, INF,12,
15                 INF,INF,0,  22, INF,INF,INF,INF,8,
16                 INF,INF,22, 0,  20, INF,INF,16, 21,
17                 INF,INF,INF,20, 0,  26, INF,7,  INF,
18                 11, INF,INF,INF,26, 0,  17, INF,INF,
19                 INF,16, INF,INF,INF,17, 0,  19, INF,
20                 INF,INF,INF,16, 7,  INF,19, 0,  INF,
21                 INF,12, 8,  21, INF,INF,INF,INF,0};
22 int main()
23 {
24     Graph *g = (Graph *)malloc(sizeof(Graph));
25     initGraph(g);
26     showGraph(g);
27     printf("\n\n");
28     Prim(g);
29 
30     return 0;
31 }
32 
33 void initGraph(Graph *g){
34    int i,j;
35    for(i=0;i<9;i++){
36         for(j=0;j<9;j++){
37             g->arc[i][j]=num[i][j];
38         }
39     }
40 }
41 void showGraph(Graph *g){
42     int i,j;
43     for(i=0;i<9;i++){
44         for(j=0;j<9;j++){
45             printf("%d ",g->arc[i][j]);
46         }
47         printf("\n");
48     }
49 }
50 
51 void Prim(Graph *g){
52     int min,i,j,k;
53     int ver[MAXSIZE];
54     int lowcost[MAXSIZE];
55     lowcost[0] = 0;
56     ver[0] = 0;
57     for(i=1;i<MAXSIZE;i++){
58         lowcost[i] = g->arc[0][i];
59         ver[i] = 0;
60     }
61     for(i=1;i<MAXSIZE;i++){
62         min = INF;
63 
64         j=1;
65         k=0;
66 
67         while(j<MAXSIZE){  //寻找生成树相连的最小权值的顶点
68             if(lowcost[j]!=0  && lowcost[j] < min){
69                 min = lowcost[j];
70                 k = j;
71             }
72 
73             j++;
74         }
75 
76         printf("(%d , %d)\n",ver[k],k);
77 
78         lowcost[k] = 0;
79 
80         for(j=1;j<MAXSIZE;j++){
81             if(lowcost[j]!=0 && g->arc[k][j] < lowcost[j]){
82                 lowcost[j] = g->arc[k][j];
83                 ver[j] = k;
84             }
85 
86         }
87     }
88 }
View Code

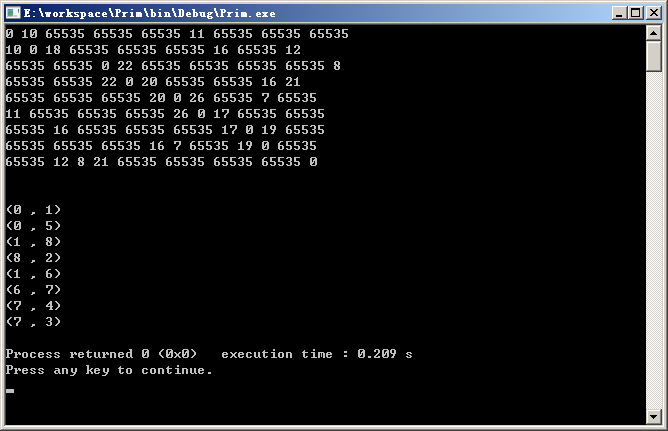
运行结果

 

 

posted @ 2014-02-07 12:03  xingoo  阅读(1140)  评论(1)  编辑  收藏  举报