cube spline---三次样条插值

插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。与拟合不用经过每个已知点不同，插值需要经过每个已知点，另外并不是阶数越高越好，因为高阶插值容易出现龙格现象，即插值后在区间两端点处波动极大，产生明显的震荡。三次样条插值作为一种常见的插值方法，这里记录一下其基本概念及求解过程。

一、基本概念

设在区间$[a, b]$上存在$n+1$个已知数据点如下，其把$[a, b]$分成了$n$个子区间$[x_0, x_1], [x_1, x_2],\ ... ,\ [x_{n-1}, x_n]$，

$$\begin{align} x &: a \le x_0 < x_1 < ...< x_n \le b \nonumber\\ f(x) = y &: \quad\quad y_0\ \quad y_1\ \quad ... \quad y_n \nonumber \end{align}$$

如果函数$S(x)$满足以下三个条件，则称$S(x)$为$f(x)$关于节点$x_0, x_1, ..., x_n$的三次样条函数。

1. 在每个子区间上都是一个不超过3次的多项式，即 $S_i(x_i) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3$；
2. 在整个区间$[a,b]$上连续且光滑，即一阶导数$S^{'}(x_i)$和二阶导数$S^{''}(x_i)$存在且连续；
3. 满足插值条件，即$S_i(x_i) = y_i,\ i = 0, 1, 2,..., n$。

二、求解过程

2.1 获取方程组

$n$个子区间中每一个都有四个未知数$(a_i, b_i, c_i, d_i)$，所以共有$4n$个未知参数需要求解。

插值条件

曲线在整个区间$[a, b]$上所有点都满足插值条件，所以$S_i(x_i) = y_i,\ i = 0, 1, 2,..., n-1,\ S_{n-1}(x_n) = y_n$，依此可得到$n+1$个方程。

曲线连续

曲线在整个区间$[a, b]$上连续，表明在端点$i = 1, 2, ... , n-1$处两边函数值相等，即：$S_{i-1}(x_i) = S_{i}(x_{i})$，其等价于$S_i(x_{i+1}) = S_{i+1}(x_{i+1}) = y_{i+1}, i = 0, 1, 2, ..., n-2$，这里可得$n-1$个方程。

曲线光滑

曲线在整个区间$[a, b]$上光滑，表明在端点$i = 1, 2, ... , n-1$两边的一阶导数和二阶导数存在且相等，即

$$S^{'}_{i-1}(x_i) = S^{'}_{i}(x_i), i = 1, 2, ..., n-1.\ S^{''}_{i-1}(x_i) = S^{''}_{i}(x_i), i = 1, 2, ..., n-1$$

其等价于

$$S^{'}_{i}(x_{i+1}) = S^{'}_{i+1}(x_{i+1}), i = 0, 1, ..., n-2.\ S^{''}_{i}(x_{i+1}) = S^{''}_{i+1}(x_{i+1}), i = 0, 1, ..., n-2$$

共$2(n-1)$个方程。

区间$[a, b]$左右两端点特性

由2.1---2.3一共可以得到$n+1 + n-1 + 2(n-1) = 4n - 2$个方程，要求解4n个未知数，还需要至少两个方程，所以这里可以考虑在两端点$i = 0, n$处的特性，加上边界处这两个方程可以对$4n$个参数进行求解。一般有三种边界条件：自然边界（Natural Spline），固定边界（Clamped Spline），非节点边界（Not-A-Knot Spline）。

• 自然边界
  指定端点二阶导数为0，即$S^{''}_0(x_0) = S^{''}_{n-1}(x_n)=0$。

• 固定边界
  人为指定端点一阶导数，这里分别定为$A$和$B$，即$S^{'}_0(x_0) = A, S^{'}_{n-1}(x_n) = B$。

• 非节点边界
  强制第一个插值点的三阶导数值等于第二个点的三阶导数值，最后第一个点的三阶导数值等于倒数第二个点的三阶导数值. 即$S^{'''}_0(x_0) = S^{'''}_1(x_1), S^{'''}_{n-2}(x_{n-1}) = S^{'''}_{n-1}(x_{n})$。

2.2 方程推导

---

由$S_i(x) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3$可得其各阶导数如下：

$S^{'}_i(x) = b_i + 2c_i(x-x_i) + 3d_i(x-x_i)^2$

$S^{''}_i(x) = 2c_i + 6d_i(x-x_i)$

$S^{'''}_i(x) = 6d_i$

---

1、由$S_i(x_i) = y_i,\ i = 0, 1, 2,..., n-1$可得：

$S_i(x_i) = a_i + b_i(x_i-x_i) + c_i(x_i-x_i)^2 + d_i(x_i-x_i)^3 = y_i$，化简可得：

$a_i = y_i \ \ \ \ \ (1)$

2、由$S_i(x_{i+1}) = y_{i+1},\ i = 0, 1, 2, ..., n - 2$可得：

$S_i(x_{i+1}) = a_i + b_i(x_{i+1}-x_i) + c_i(x_{i+1}-x_i)^2 + d_i(x_{i+1}-x_i)^3 = y_{i+1}$，令$h_i = x_{i+1}-x_i$，则可简写为

$a_i + b_ih_i + c_ih^2_i + d_ih^3_i = y_{i+1} \ \ \ \ \ (2)$

3、由$S^{'}_{i}(x_{i+1}) = S^{'}_{i+1}(x_{i+1}), i = 0, 1, ..., n-2$可得：

$S^{'}_i(x_{i+1}) = b_i + 2c_i(x_{i+1}-x_i) + 3d_i(x_{i+1}-x_i)^2 = b_i + 2c_ih_i + 3d_ih^2_i$

$S^{'}_{i+1}(x_{i+1}) = b_{i+1} + 2c_{i+1}(x_{i+1}-x_{i+1}) + 3d_{i+1}(x_{i+1}-x_{i+1})^2 = b_{i+1}$

所以

$b_i + 2c_ih_i + 3d_ih^2_i - b_{i+1} = 0 \ \ \ \ \ (3)$

4、由$S^{''}_{i}(x_{i+1}) = S^{''}_{i+1}(x_{i+1}), i = 0, 1, ..., n-2$可得

$2c_i + 6d_ih_i - 2C_{i+1} = 0 \ \ \ \ \ (4)$

---

通过(2)(3)(4)式可知$b_i, c_i, d_i$存在某种关系，为了方便求解，这里作以下变换，将$b_i, c_i, d_i$三个参数变换为求解$m_i$一个参数。
由(4)式可知：

$d_i = \frac{2C_{i+1} - 2C_{i}}{6h_i}$, 令$2C_i = m_i$,则：

$d_i = \frac{m_{i+1} - m_{i}}{6h_i}$

由(2)式可知：

$a_i + b_ih_i + c_ih^2_i + d_ih^3_i = y_{i+1} = y_i + h_ib_i + h^2_i\frac{m_i}{2} + h^3_i\frac{m_{i+1} - m_i}{6h_i}$，化简可得：

$b_i = \frac{y_{i+1} - y_i}{h_i} = \frac{h_i}{2}m_i - \frac{h_i}{6}(m_{i+1} - m_i)$

将$b_i, c_i, d_i$代入(3)式可知：

$h_im_i + 2(h_i + h_{i+1})m_{i+1} + h_{i+1}m_{i+2} = 6(\frac{y_{i+2} - y_{i+1}}{h_{i+1}} - \frac{y_{i+1} - y_i}{h_i}), i = 0, 1, ..., n-2.$

---

通过以上推导可知关于$m_i$的一个方程组，维度为$n-1$，再考虑边界条件便可以得到$n+1$个方程，进而进行求解。
自然边界

由$S^{''}_0(x_0) = S^{''}_{n-1}(x_n)=0$可知$m_0 = m_n = 0$，因此方程组可以写成以下形式

$$\begin{bmatrix} 1 & 0 & 0 & 0 & 0 & \cdots & 0 \\ h_0 & 2(h_0 + h_1) & h_1 & 0 & 0 & \cdots & 0 \\ 0 & h_1 & 2(h_1 + h_2) & h_2 & 0 & \cdots & 0 \\ 0 & 0 & h_2 & 2(h_2 + h3) & h_3 & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & h_{n-2} & 2(h_{n-2} + h_{n-1}) & h_{n-1} \\ 0 & 0 & 0 & \cdots & 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} m_0 \\ m_1 \\ m_2 \\ m_3 \\ \vdots \\ m_{n-1} \\ m_n \\ \end{bmatrix} = 6\begin{bmatrix} 0 \\ \frac{y_2 - y_1}{h_1} - \frac{y_1 - y_0}{h_0} \\ \frac{y_3 - y_2}{h_2} - \frac{y_2 - y_1}{h_1} \\ \frac{y_4 - y_3}{h_3} - \frac{y_3 - y_2}{h_2} \\ \vdots \\ \frac{y_n - y_{n-1}}{h_{n-1}} - \frac{y_{n-1} - y_{n-2}}{h_{n-2}} \\ 0 \\ \end{bmatrix}$$

固定边界

由$S^{'}_0(x_0) = A$可知：

$$\begin{align} A &= b_0 \nonumber\\ &= \frac{y_1 - y_0}{h_0} - \frac{h_0}{2}m_0 - \frac{h_0}{6}(m_1 - m_0) \nonumber \end{align}$$

变形可得：

$2h_0m_0 + h_0m_1 = 6[\frac{y_1 - y_0}{h_0} - A]$

由$S^{'}_{n-1}(x_n) = B$可知：

$$\begin{align} B &= b_{n-1} \nonumber\\ &= \frac{y_n - y_{n-1}}{h_{n-1}} - \frac{h_{n-1}}{2}m_{n-1} - \frac{h_{n-1}}{6}(m_n - m_{n-1}) \nonumber \end{align}$$

所以：

$h_{n-1}m_{n-1} + 2h_{n-1}m_n = 6[B - \frac{y_n - y_{n-1}}{h_{n-1}}]$

因此方程组的系数矩阵可以改写为

$$\begin{bmatrix} 2h_0 & h_0 & 0 & 0 & 0 & \cdots & 0 \\ h_0 & 2(h_0 + h_1) & h_1 & 0 & 0 & \cdots & 0 \\ 0 & h_1 & 2(h_1 + h_2) & h_2 & 0 & \cdots & 0 \\ 0 & 0 & h_2 & 2(h_2 + h3) & h_3 & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & h_{n-2} & 2(h_{n-2} + h_{n-1}) & h_{n-1} \\ 0 & 0 & 0 & \cdots & 0 & h_{n-1} & 2h_{n-1} \\ \end{bmatrix} \begin{bmatrix} m_0 \\ m_1 \\ m_2 \\ m_3 \\ \vdots \\ m_{n-1} \\ m_n \\ \end{bmatrix} = 6\begin{bmatrix} \frac{y_1 - y_0}{h_0} - A \\ \frac{y_2 - y_1}{h_1} - \frac{y_1 - y_0}{h_0} \\ \frac{y_3 - y_2}{h_2} - \frac{y_2 - y_1}{h_1} \\ \frac{y_4 - y_3}{h_3} - \frac{y_3 - y_2}{h_2} \\ \vdots \\ \frac{y_n - y_{n-1}}{h_{n-1}} - \frac{y_{n-1} - y_{n-2}}{h_{n-2}} \\ B - \frac{y_n - y_{n-1}}{h_{n-1}} \\ \end{bmatrix}$$

非节点边界

由于$S^{'''}_0(x_0) = S^{'''}_1(x_1), S^{'''}_{n-2}(x_{n-1}) = S^{'''}_{n-1}(x_{n})$且$S^{'''}_{i}(x_{i}) = 6d_i$，所以：

$d_0 = d_1,\ d_{n-2} = d_{n-1}$，另外由$d_i = \frac{m_{i+1} - m_i}{6h_i}$，所以

$h_1(m_1 - m_0) = h_0(m_2 - m_1), \ h_{n-1}(m_{n-1} - m_{n-2}) = h_{n-2}(m_{n} - m_{n-1})$

变形可得：

$$\begin{align} -h_1m_0 + (h_0 + h_1)m_1 - h_0m_1 &= 0 \nonumber\\ -h_{n-1}m_{n-2} + (h_{n-2} + h_{n-1})m_{n-1} - h_{n-2}m_n &= 0 \nonumber \end{align}$$

因此方程组的系数矩阵可以改写为

$$\begin{bmatrix} -h_1 & h_0 + h_1 & - h_0 & 0 & 0 & \cdots & 0 \\ h_0 & 2(h_0 + h_1) & h_1 & 0 & 0 & \cdots & 0 \\ 0 & h_1 & 2(h_1 + h_2) & h_2 & 0 & \cdots & 0 \\ 0 & 0 & h_2 & 2(h_2 + h3) & h_3 & \cdots & \vdots \\ \vdots & \vdots & \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & h_{n-2} & 2(h_{n-2} + h_{n-1}) & h_{n-1} \\ 0 & 0 & 0 & \cdots & -h_{n-1} & h_{n-2} + h_{n-1} & - h_{n-2} \\ \end{bmatrix} \begin{bmatrix} m_0 \\ m_1 \\ m_2 \\ m_3 \\ \vdots \\ m_{n-1} \\ m_n \\ \end{bmatrix} = 6\begin{bmatrix} 0 \\ \frac{y_2 - y_1}{h_1} - \frac{y_1 - y_0}{h_0} \\ \frac{y_3 - y_2}{h_2} - \frac{y_2 - y_1}{h_1} \\ \frac{y_4 - y_3}{h_3} - \frac{y_3 - y_2}{h_2} \\ \vdots \\ \frac{y_n - y_{n-1}}{h_{n-1}} - \frac{y_{n-1} - y_{n-2}}{h_{n-2}} \\ 0 \\ \end{bmatrix}$$

三、算法总结

• 步骤1：分区间
  将数据分成不同子区间$[x_0, x_1], [x_1, x_2],\ ... ,\ [x_{n-1}, x_n]$

• 步骤2：计算步长
  计算步长$h_i = x_{i+1} - x_{i}$

• 步骤3：求解方程组获得$m_i$

• 步骤4：计算每个子区间的参数${a_i, b_i, c_i, d_i}$
  $a_i = y_i$
  $b_i = \frac{y_{i+1} - y_i}{h_i} - \frac{h_i}{2}m_i - \frac{h_i}{6}(m_{i+1} - m_i)$
  $c_i = \frac{m_i}{2}$
  $d_i = \frac{m_{i+1} - m_{i}}{6h_i}$

• 步骤5： 得到每个区间样条函数
  $S_i(x_i) = a_i + b_i(x-x_i) + c_i(x-x_i)^2 + d_i(x-x_i)^3$

四、示例结果

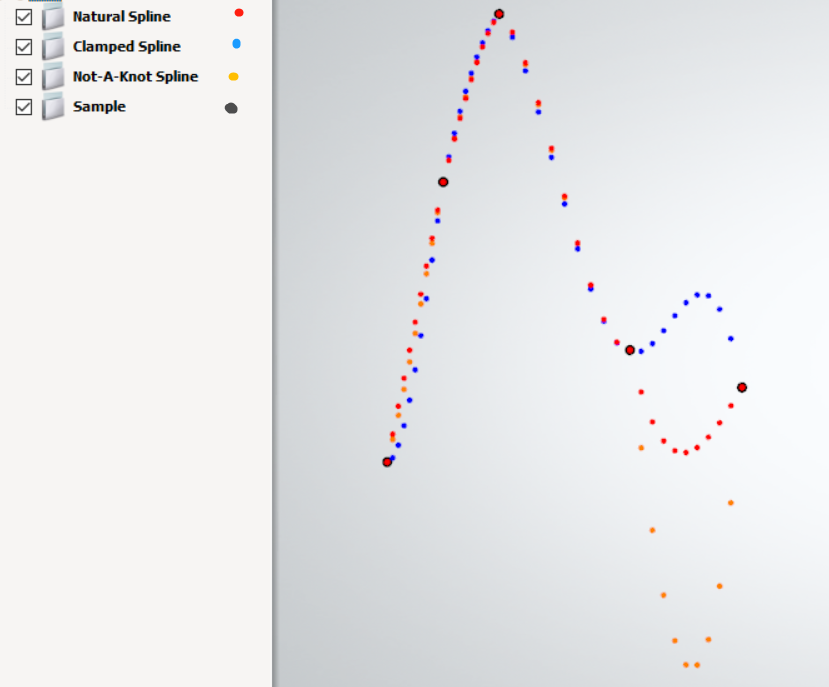
样本$(4.0, 4.2), (4.3, 5.7), (4.6, 6.6), (5.3, 4.8), (5.9, 4.6)$在不同边界情况下插值效果如下：

五、代码实现

参考三次样条插值(Cubic Spline Interpolation)及代码实现(C语言)

点击展开代码

#define S_FUNCTION_NAME  cubic
#define S_FUNCTION_LEVEL 2
#include "simstruc.h"
#include "malloc.h"  //方便使用变量定义数组大小

static void mdlInitializeSizes(SimStruct *S)
{
    /*参数只有一个，是n乘2的定点数组[xi, yi]:
     * [ x1，y1;
     *   x2, y2;
     *   ..., ...;
     *   xn, yn;
    */
    ssSetNumSFcnParams(S, 1); 
    if (ssGetNumSFcnParams(S) != ssGetSFcnParamsCount(S)) return;

    ssSetNumContStates(S, 0);
    ssSetNumDiscStates(S, 0);

    if (!ssSetNumInputPorts(S, 1)) return;  //输入是x
    ssSetInputPortWidth(S, 0, 1);
    ssSetInputPortRequiredContiguous(S, 0, true);
    ssSetInputPortDirectFeedThrough(S, 0, 1);

    if (!ssSetNumOutputPorts(S, 1)) return;  //输出是S(x)
    ssSetOutputPortWidth(S, 0, 1);

    ssSetNumSampleTimes(S, 1);
    ssSetNumRWork(S, 0);
    ssSetNumIWork(S, 0);
    ssSetNumPWork(S, 0);
    ssSetNumModes(S, 0);
    ssSetNumNonsampledZCs(S, 0);

    ssSetSimStateCompliance(S, USE_DEFAULT_SIM_STATE);

    ssSetOptions(S, 0);
}

static void mdlInitializeSampleTimes(SimStruct *S)
{
    ssSetSampleTime(S, 0, CONTINUOUS_SAMPLE_TIME);
    ssSetOffsetTime(S, 0, 0.0);
}



#define MDL_INITIALIZE_CONDITIONS
#if defined(MDL_INITIALIZE_CONDITIONS)
  static void mdlInitializeConditions(SimStruct *S)
  {
  }
#endif



#define MDL_START
#if defined(MDL_START) 
  static void mdlStart(SimStruct *S)
  {
  }
#endif /*  MDL_START */


static void mdlOutputs(SimStruct *S, int_T tid)
{
    const real_T *map = mxGetPr(ssGetSFcnParam(S,0));  //获取定点数据
    const int_T *mapSize = mxGetDimensions(ssGetSFcnParam(S,0));  //定点数组维数
    const real_T *x = (const real_T*) ssGetInputPortSignal(S,0);  //输入x
    real_T       *y = ssGetOutputPortSignal(S,0); //输出y
    int_T step = 0;  //输入x在定点数中的位置
    int_T i;
    real_T yval;

    for (i = 0; i < mapSize[0]; i++)
    {
        if (x[0] >= map[i] && x[0] < map[i + 1])
        {
            step = i;
            break;
        }
    }
    
    cubic_getval(&yval, mapSize, map, x[0], step);
    y[0] = yval;
    
}

//自然边界的三次样条曲线函数
void cubic_getval(real_T* y, const int_T* size, const real_T* map, const real_T x, const int_T step)
{
    int_T n = size[0];
    
    //曲线系数
    real_T* ai = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* bi = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* ci = (real_T*)malloc(sizeof(real_T) * (n-1));
    real_T* di = (real_T*)malloc(sizeof(real_T) * (n-1));
    
    real_T* h = (real_T*)malloc(sizeof(real_T) * (n-1));  //x的??
    
    /* M矩阵的系数
     *[B0, C0, ...
     *[A1, B1, C1, ...
     *[0,  A2, B2, C2, ...
     *[0, ...             An-1, Bn-1]
     */
    real_T* A = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* B = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* C = (real_T*)malloc(sizeof(real_T) * (n-2));
    real_T* D = (real_T*)malloc(sizeof(real_T) * (n-2)); //等号右边的常数矩阵
    real_T* E = (real_T*)malloc(sizeof(real_T) * (n-2)); //M矩阵
    
    real_T* M = (real_T*)malloc(sizeof(real_T) * (n));  //包含端点的M矩阵
    
    int_T i;
    
    //计算x的步长
    for ( i = 0; i < n -1; i++)
    {
        h[i] = map[i + 1] - map[i];
    }
    
    //指定系数
    for( i = 0; i< n - 3; i++)
    {
        A[i] = h[i]; //忽略A[0]
        B[i] = 2 * (h[i] + h[i+1]);
        C[i] = h[i+1]; //忽略C(n-1)
    }

    
    //指定常数D
    for (i = 0; i<n - 3; i++)
    {
        D[i] = 6 * ((map[n + i + 2] - map[n + i + 1]) / h[i + 1] - (map[n + i + 1] - map[n + i]) / h[i]);
    }
    
    
    //求解三对角矩阵，结果赋值给E
    TDMA(E, n-3, A, B, C, D);
    
    M[0] = 0; //自然边界的首端M为0
    M[n-1] = 0;  //自然边界的末端M为0
    for(i=1; i<n-1; i++)
    {
        M[i] = E[i-1]; //其它的M值
    }
    
    //?算三次?条曲?的系数
    for( i = 0; i < n-1; i++)
    {
        ai[i] = map[n + i];
        bi[i] = (map[n + i + 1] - map[n + i]) / h[i] - (2 * h[i] * M[i] + h[i] * M[i + 1]) / 6;
        ci[i] = M[i] / 2;
        di[i] = (M[i + 1] - M[i]) / (6 * h[i]);
    }
    
    *y = ai[step] + bi[step]*(x - map[step]) + ci[step] * (x - map[step]) * (x - map[step]) + di[step] * (x - map[step]) * (x - map[step]) * (x - map[step]);
    
    free(h);
    free(A);
    free(B);
    free(C);
    free(D);
    free(E);
    free(M);
    free(ai);
    free(bi);
    free(ci);
    free(di);

}

void TDMA(real_T* X, const int_T n, real_T* A, real_T* B, real_T* C, real_T* D)
{
    int_T i;
    real_T tmp;

    //上三角矩阵
    C[0] = C[0] / B[0];
    D[0] = D[0] / B[0];

    for(i = 1; i<n; i++)
    {
        tmp = (B[i] - A[i] * C[i-1]);
        C[i] = C[i] / tmp;
        D[i] = (D[i] - A[i] * D[i-1]) / tmp;
    }

    //直接求出X的最后一个值
    X[n-1] = D[n-1];

    //逆向迭代， 求出X
    for(i = n-2; i>=0; i--)
    {
        X[i] = D[i] - C[i] * X[i+1];
    }
}


#define MDL_UPDATE 
#if defined(MDL_UPDATE)
  static void mdlUpdate(SimStruct *S, int_T tid)
  {
  }
#endif

#define MDL_DERIVATIVES
#if defined(MDL_DERIVATIVES)
  static void mdlDerivatives(SimStruct *S)
  {
  }
#endif

static void mdlTerminate(SimStruct *S)
{
}

#ifdef  MATLAB_MEX_FILE  
#include "simulink.c"
#else
#include "cg_sfun.h"
#endif

参考链接

三次样条插值(Cubic Spline Interpolation)及代码实现(C语言)
三次样条（cubic spline）插值