水友赛 解题报告

题目描述

给定一个 \(n\) 个点的树，每一个点有点权 \(a_i\)。
我们称一条树上简单路径对应的序列为序列中的第 \(i\) 项的值为路径中第 \(i\) 个点的点权。
现在对于每一条树上简单路径对应的序列求 LIS，问 LIS 最大值。
数据范围：\(n \le 2\times 10^5,a_i \le 10^6\)。保证不卡常。

分析

首先我们想到，对于任意一条路径，我们都可以在路径两端的 LCA 处处理，因为我们并不关心你的两端是谁，我们只关心你对答案的贡献是多少。

那么现在只需要考虑怎么在一个点进行答案统计和信息维护即可。

注意到这是一个关于子树的问题，我们有两个解题思路：树上启发式合并和线段树合并。

这里考虑后者，因为前者我不熟。

首先你需要知道：对于一个 LIS 序列，如果从中间断开，分别往两侧走，你会发现一边是上升序列，一边是下降序列。

那么我们只需要维护以某一个点权结尾的最长上升序列和最长下降序列的长度即可。

那你可能会想到：对于当前点 \(u\)，这个节点的答案为以 \([1,a_u-1]\) 内的点权结尾的 LIS 长度加上以 \([a_u+1,V]\) 内点权开头的 LDS 长度再加一。

但这对吗？你是 LCA，你就一定要出现在这条路径的 LIS 上吗？请看下图，很明显，LIS为 $ 4 \rightarrow 2 \rightarrow 3 \rightarrow 5$，和当 LCA 的 \(1\) 一点关系没有。因此不能这么统计。

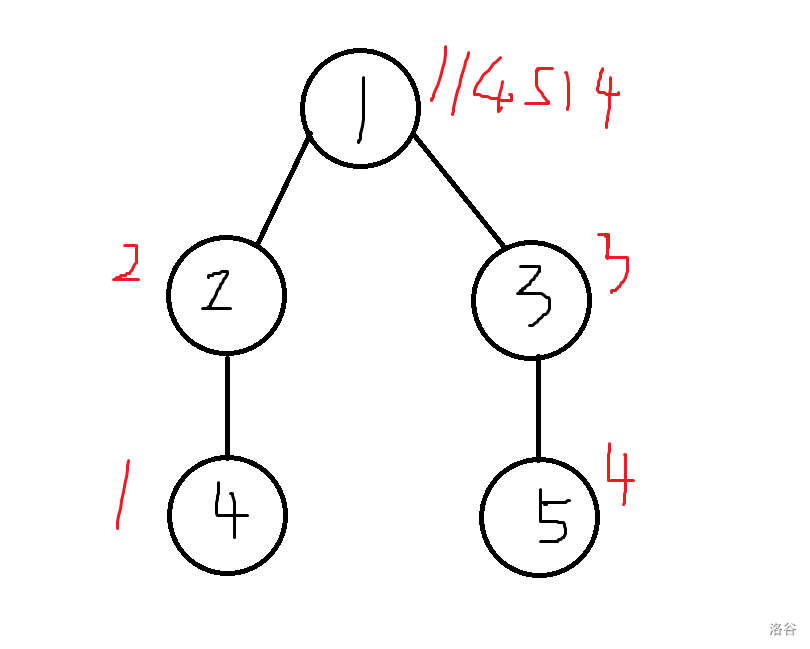
那么怎么统计答案呢？我们考虑答案一定是形如：“以 \([1,x]\) 内的点权结尾的 LIS 长度加上以 \([y,V]\) 内点权开头的 LDS 长度（满足 \(x < y\)）”。这可以在线段树合并内解决，即在处理要合并的节点对时，就将一个节点的左儿子的 LIS 长度和另外一个节点的右儿子的 LDS 长度求和，最大值即为答案。

证明：这么统计的答案一定是合法且不漏的

    首先证明答案合法：这是容易证明的，因为左儿子维护的区间一定在右儿子维护的区间的左边且两者无交。因此一定满足偏序关系。   
    其次证明答案不漏：因为产生新的答案一定是由原来的两棵线段树上的节点凑成的，所以产生最大值的节点在两棵线段树上都有节点，那么就一定会在线段树合并时被访问到。  
    Q.E.D.  
    

时间复杂度分析读者不难自证，给出结论：\(O(nlog^2n)\)。

代码

const int N=4e5+100,M=N*120;
int n,m,a[N],rk[N];
struct Edge{int from,to;}e[N<<1];
int num,h[N];
void add(int f,int t){e[++num].from=h[f],e[num].to=t,h[f]=num;}
void init(){
    For(i,1,n) rk[i]=a[i];
    sort(rk+1,rk+n+1,less<int>());
    m=unique(rk+1,rk+n+1)-rk-1;
    For(i,1,n) a[i]=lower_bound(rk+1,rk+m+1,a[i])-rk;
}
int rt[N<<1],ls[M],rs[M],val1[M],cnt,val2[M];
void update1(int &i,int l,int r,int x,int k){
    if(!i) i=++cnt;
    val1[i]=max(val1[i],k);
    if(l==r) return;
    int mid=l+r>>1;
    if(x<=mid)
        update1(ls[i],l,mid,x,k);
    else
        update1(rs[i],mid+1,r,x,k);
}
int query1(int i,int l,int r,int x,int y){
    if(!i || x>y) return 0;
    if(x<=l && r<=y)
        return val1[i];
    int mid=l+r>>1;
    if(x>mid) return query1(rs[i],mid+1,r,x,y);
    if(mid>=y) return query1(ls[i],l,mid,x,y);
    return max(query1(ls[i],l,mid,x,y),query1(rs[i],mid+1,r,x,y));
}
void update2(int &i,int l,int r,int x,int k){
    if(!i) i=++cnt;
    val2[i]=max(val2[i],k);
    if(l==r) return;
    int mid=l+r>>1;
    if(x<=mid)
        update2(ls[i],l,mid,x,k);
    else
        update2(rs[i],mid+1,r,x,k);
}
int query2(int i,int l,int r,int x,int y){
    if(!i || x>y) return 0;
    if(x<=l && r<=y)
        return val2[i];
    int mid=l+r>>1;
    if(x>mid) return query2(rs[i],mid+1,r,x,y);
    if(mid>=y) return query2(ls[i],l,mid,x,y);
    return max(query2(ls[i],l,mid,x,y),query2(rs[i],mid+1,r,x,y));
}
int ans=0;
int Merge(int x,int y){
    if(!x || !y) return x|y;
    ckmx(ans,val1[ls[x]]+val2[rs[y]]);
    ckmx(ans,val1[ls[y]]+val2[rs[x]]);
    val1[x]=max(val1[x],val1[y]);
    val2[x]=max(val2[x],val2[y]);
    ls[x]=Merge(ls[x],ls[y]);
    rs[x]=Merge(rs[x],rs[y]);
    return x;
}
void dfs(int u,int fa){
    int mxu=0,mxd=0,mmxu,mmxd;
    for(int i=h[u];i;i=e[i].from){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        mmxu=query1(rt[v],1,m,1,a[u]-1);
        mmxd=query2(rt[v],1,m,a[u]+1,m);
        ckmx(ans,max(mmxu+mxd+1,mmxd+mxu+1));
        ckmx(mxu,mmxu);
        ckmx(mxd,mmxd);
        rt[u]=Merge(rt[u],rt[v]);
    }
    update1(rt[u],1,m,a[u],mxu+1);
    update2(rt[u],1,m,a[u],mxd+1);
}
int main()
{
    n=read();
    For(i,1,n) a[i]=read();
    init();
    int u,v;
    For(i,2,n) u=read(),v=read(),add(u,v),add(v,u);
    dfs(1,0);
    printf("%d",ans),assert(ans<=m);
    return 0;
}