CF538G Berserk Robot 解题报告
CF538G Berserk Robot 解题报告
题意简述
给定一个长为 \(l\) 的移动指令序列,指令字符集为 UDLR ,每个指令会让机器人往对应方向移动一个单位。现在告诉你 \(m\) 条形如 \((t_i,x_i,y_i)\) 的信息,代表机器人在 \(t_i\) 时刻位于 \((x_i,y_i)\)。请构造一个符合所有信息的指令序列,或报告无解。
数据范围:\(m \le 10^5\),\(n \le 10^6\),\(t_i,|x_i|,|y_i| \le 10^{18}\)
分析
本题有若干非常经典的Trick。
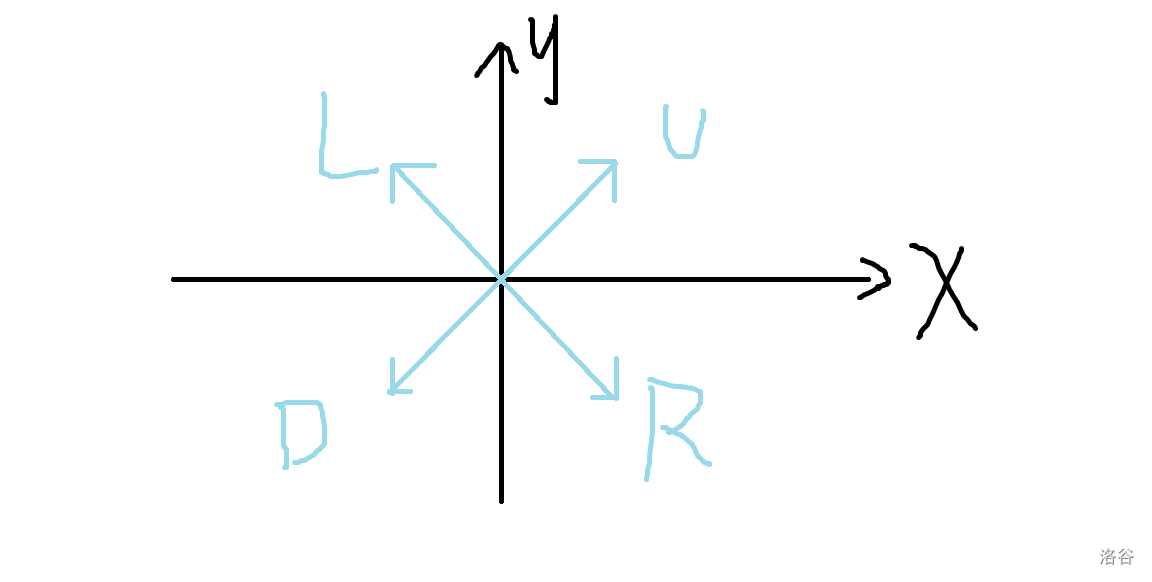
首先看到 UDLR ,就要想到给坐标轴逆时针旋转 \(45\) 度。这样 UDLR 就坐标变化就分别变为 \((+1,+1)\),\((-1.-1)\),\((-1,+1)\),\((+1,-1)\)(参考下图)。通过这种方式,我们就将 \(x\) 轴和 \(y\) 轴独立开来,可以分别处理。在这样处理下,坐标变成 \((x_i+y_i,y_i-x_i)\)。
但是这样还不够简便,因为在同一维中 \(+1\) 和 \(-1\) 可以抵消掉,还是太难思考了。
我们考虑引入时间维:因为无论操作选择 \(+1\) 还是 \(-1\),在时间上都 \(+1\) 了,因此我们可以把这两者结合起来,把操作变成 \(0\) 和 \(+2\),把目标坐标变成 \((x_i+y_i+t_i,y_i-x_i+t_i)\)。但是 \(+2\) 有点奇怪,而且我们发现坐标的两维都是可以被 \(2\) 整除的(因为两维坐标和与时间的奇偶性相同)。
最后我们把操作转换为 \(0\) 和 \(+1\),目标的位置为 $\Large(\frac{x_i+y_i+t_i}{2},\frac{y_i-x_i+t_i}{2}) $。
接下来我们分析这问题的操作具有周期性,于是我们考虑假设已经一个周期的影响,即假设我们已知一个操作周期后机器人会在两维分别移动 \(v_x\) 和 \(v_y\) 之后来列式。我们假设 \(k_i = \lfloor \frac{t_i}{l} \rfloor\),\(w_i= t_i \bmod l\)。我们按 \(w\) 升序对点进行排序,为了使每一个点的限制都被统计到,我们加入 \(k_i=0,w_i=0\) 和 \(k_i=-1,w_i=l\),容易发现这两种情况都是 \(x_i=0,y_i=0,t_i=0\) 的。
对于 \(w\) 中相邻两个点,我们令 \(j=i+1\)。为了讨论在一个周期内的操作,我们(以 \(x\) 轴为例)设 \(x_i'=x_i-k*v_x\),令 \(k=k_j-k_i\) ,\(w=w_j-w_i\),那么对于 \(i\) 和 \(j\),他们可以转移,当且仅当:
带入各类数值,就可以得到若干不等式,最后得到解集。选择解集中任意一个点进行构造。
在构造时,我们可以先尽快到达下一个点,如果有多余的步数,就在下一个点附近左右横跳即可。
代码
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
#define Inf (1ll<<60)
#define For(i,s,t) for(int i=s;i<=t;++i)
#define Down(i,s,t) for(int i=s;i>=t;--i)
#define ls (i<<1)
#define rs (i<<1|1)
#define add(x,y) (1ll*(x)+(y))%mod
#define lowbit(x) ((x)&(-(x)))
#define End {printf("NO\n");exit(0);}
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
inline int min(int x,int y){return x<y?x:y;}
inline int max(int x,int y){return x>y?x:y;}
inline ll min(ll x,ll y){return x<y?x:y;}
inline ll max(ll x,ll y){return x>y?x:y;}
inline int read(){
register int x=0,f=1;
char c=getchar();
while(c<'0' || '9'<c) f=(c=='-')?-1:1,c=getchar();
while('0'<=c && c<='9') x=(x<<1)+(x<<3)+c-'0',c=getchar();
return x*f;
}
void write(int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
const int N=2e5+100;
int n,l;
//其中,x,y是经过变换后的坐标,k是经过的周期数,w是该点在一个周期中的位置
struct Node{ll t,x,y,k;int w;}q[N];
bool cmp(Node x,Node y){return x.w<y.w;}
//x的取值范围是[lx,rx],y的取值范围是[ly,ry]
ll lx,rx,ly,ry;
int main()
{
//freopen("test.in","r",stdin);
//freopen("test.out","w",stdout);
n=read(),l=read();
For(i,1,n){
scanf("%lld%lld%lld",&q[i].t,&q[i].x,&q[i].y);
//奇偶性判断
//printf("%lld\n",q[i].x ^ q[i].y ^ q[i].t);
if((q[i].x ^ q[i].y ^ q[i].t) & 1) End
ll nx,ny;
nx=(q[i].x+q[i].y+q[i].t)/2;
ny=(q[i].y-q[i].x+q[i].t)/2;
q[i].x=nx,q[i].y=ny;
q[i].k=q[i].t/l;
q[i].w=q[i].t%l;
}
//printf("Nothing\n");
sort(q+1,q+n+1,cmp);
q[++n].k=-1,q[n].w=l;
lx=ly=-inf,rx=ry=inf;
For(i,1,n){
ll k=q[i].k-q[i-1].k;
int w=q[i].w-q[i-1].w;
if(!k){
if(q[i].x-q[i-1].x-w>0 || q[i].x-q[i-1].x<0) End
if(q[i].y-q[i-1].y-w>0 || q[i].y-q[i-1].y<0) End
}
else if(k>0){
lx=max(lx, (ll)ceil(1.0L*(q[i].x-q[i-1].x-w)/k) );
rx=min(rx, (ll)floor(1.0L*(q[i].x-q[i-1].x)/k));
ly=max(ly, (ll)ceil(1.0L*(q[i].y-q[i-1].y-w)/k));
ry=min(ry, (ll)floor(1.0L*(q[i].y-q[i-1].y)/k));
}
else{
k=-k;
lx=max(lx, (ll)ceil(1.0L*(q[i-1].x-q[i].x)/k) );
rx=min(rx, (ll)floor(1.0L*(w+q[i-1].x-q[i].x)/k));
ly=max(ly, (ll)ceil(1.0L*(q[i-1].y-q[i].y)/k));
ry=min(ry, (ll)floor(1.0L*(w+q[i-1].y-q[i].y)/k));
}
}
//cout<<lx<<' '<<rx<<' '<<ly<<' '<<ry<<'\n';
if(lx>rx || ly>ry) End
For(i,1,n){
int dx=(q[i].x - q[i].k*lx)-(q[i-1].x - q[i-1].k*lx);
int dy=(q[i].y - q[i].k*ly)-(q[i-1].y - q[i-1].k*ly);
int tim=q[i].w-q[i-1].w,x=0,y=0;
while(tim){
if(x<dx){
x++;
if(y<dy) putchar('U'),y++;
else putchar('R');
}
else{
if(y<dy) putchar('L'),y++;
else putchar('D');
}
--tim;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号