洛谷 P14944 已经没有什么好构造的了 题解

Solution

不难发现，凸多边形最多有 \(3\) 个锐角。因此对于 \(m>3\) 显然无解。否则分讨 \(m\) 的取值，构造方法如下图所示，红线代表一段凸壳。

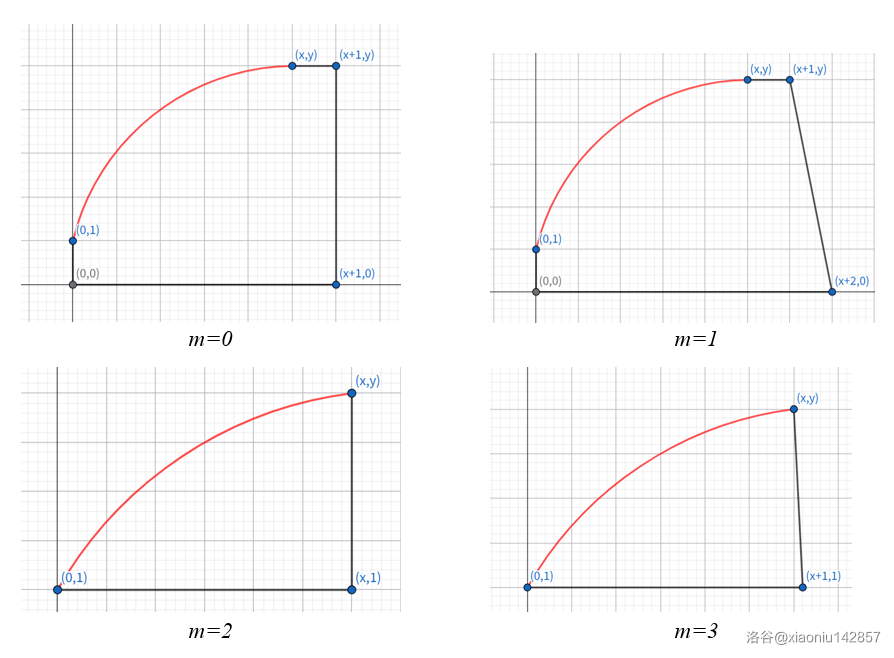
这样问题就变成了如何构造红色的凸壳部分。由于只能用整点，因此凸壳中线段斜率均为有理数。

这启发我们构造一串不同的正斜率并从大到小排序。具体做法就是枚举所有满足 \(1\le p,q\le K\) 的 \(\frac{p}{q}\)，约分，排序并去重。发现 \(K=406\) 时就能得到至少 \(10^5\) 个不同斜率。

我们还需要证明这样做不会超出 \(10^8\) 的值域限制。由于凸壳中不超过 \(n\) 条线段，每条线段对 \(x,y\) 坐标的贡献均 \(\le K\)，因此右上角的点的 \(x,y\) 坐标均不会超过 \(nK\le 4.06\times 10^7<10^8\)，证毕。

注意特判掉 \(n\le 4\) 的情况。

Code

#include <bits/stdc++.h>
#define rept(i,a,b) for(int i(a);i<=b;++i)
#define fi first
#define se second
#define pii pair<int,int>
using namespace std;
constexpr int K=406,N=K*K+5;
struct Frac{
    int a,b;
    Frac(int _a=0,int _b=1):a(_a),b(_b){
        int g=gcd(a,b);a/=g,b/=g;
    }
    inline bool operator<(const Frac &rhs) const {
        return a*rhs.b<rhs.a*b;
    }
    inline bool operator==(const Frac &rhs) const {
        return a==rhs.a&&b==rhs.b;
    }
}s[N];
int T,n,m,cnt;
const vector<pii> get_convex_hull(int e){  // 返回包含e条边，左下角为(0,1)的凸壳上的点，逆时针顺序
    vector<pii> res;
    pii cur(0,1);
    res.emplace_back(cur);
    rept(i,1,e){
        cur.fi+=s[i].a;
        cur.se+=s[i].b;
        res.emplace_back(cur);
    }
    reverse(res.begin(),res.end());
    return res;
}
signed main(){
    scanf("%d",&T);
    rept(i,1,K) rept(j,1,K) s[++cnt]=Frac(i,j);
    sort(s+1,s+cnt+1);
    cnt=unique(s+1,s+cnt+1)-s-1;
    while(T--){
        scanf("%d%d",&n,&m);
        if(n==3){
            switch(m){
                case 2:printf("0 0\n1 0\n0 1\n");break;
                case 3:printf("0 0\n2 0\n1 2\n");break;
                default:printf("scare\n");
            }
        }else if(n==4){
            switch(m){
                case 0:printf("0 0\n1 0\n1 1\n0 1\n");break;
                case 1:printf("1 0\n3 1\n1 2\n0 1\n");break;
                case 2:printf("1 0\n2 0\n0 2\n0 1\n");break;
                case 3:printf("3 0\n6 4\n3 5\n0 4\n");break;
                default:printf("scare\n");
            }
        }else{
            vector<pii> res;
            int x,y;
            switch(m){
                case 0:
                    res=get_convex_hull(n-4);
                    x=res[0].fi,y=res[0].se;
                    printf("0 0\n%d 0\n%d %d\n",x+1,x+1,y);
                    for(auto [x,y]:res) printf("%d %d\n",x,y);
                    break;
                case 1:
                    res=get_convex_hull(n-4);
                    x=res[0].fi,y=res[0].se;
                    printf("0 0\n%d 0\n%d %d\n",x+2,x+1,y);
                    for(auto [x,y]:res) printf("%d %d\n",x,y);
                    break;
                case 2:
                    res=get_convex_hull(n-2);
                    x=res[0].fi,y=res[0].se;
                    printf("%d 1\n",x);
                    for(auto [x,y]:res) printf("%d %d\n",x,y);
                    break;
                case 3:
                    res=get_convex_hull(n-2);
                    x=res[0].fi,y=res[0].se;
                    printf("%d 1\n",x+1);
                    for(auto [x,y]:res) printf("%d %d\n",x,y);
                    break;
                default:
                    printf("scare\n");
            }
        }
    }
    return 0;
}