洛谷 P3650 [USACO1.3] 滑雪课程设计 Ski Course Design 题解

题意概述

给定一个长度为 \(n\) 的数列 \(\{a_i\}\)，将 \(a_i\) 改为 \(b\) 所需的代价是 \((a_i-b)^2\)。求使得 \(\max\{a_i\}-\min\{a_i\}\le17\) 所需的最小代价。

解题思路

考虑三分法。

如果不会三分法，右转 OI Wiki 学一学。

设要将数列的所有元素修改到 \([x,x+17]\) 区间内，则代价即为关于 \(x\) 的函数 \(f(x)\)。问题转化求 \(f(x)\) 在 \([\min\{a_i\},\max\{a_i\}-17]\) 区间上的最小值。显然，若 \([x,x+17]\) 的范围超出了数列的取值范围，则一定不会更优。

由题意得：

\[f(x)=\sum_{i = 1}^{n}cost_i(x) \]

其中 \(cost_i(x)\) 为元素 \(a_i\) 产生的代价，是关于 \(x\) 的函数，为：

\[cost_i(x)= \begin{cases} (a_i - x)^2&(a_i<x),\\ 0&(x\leq a_i\leq x + 17),\\ (a_i - x - 17)^2&(a_i>x + 17). \end{cases} \]

\(cost_i(x)\) 的图像如下图所示：

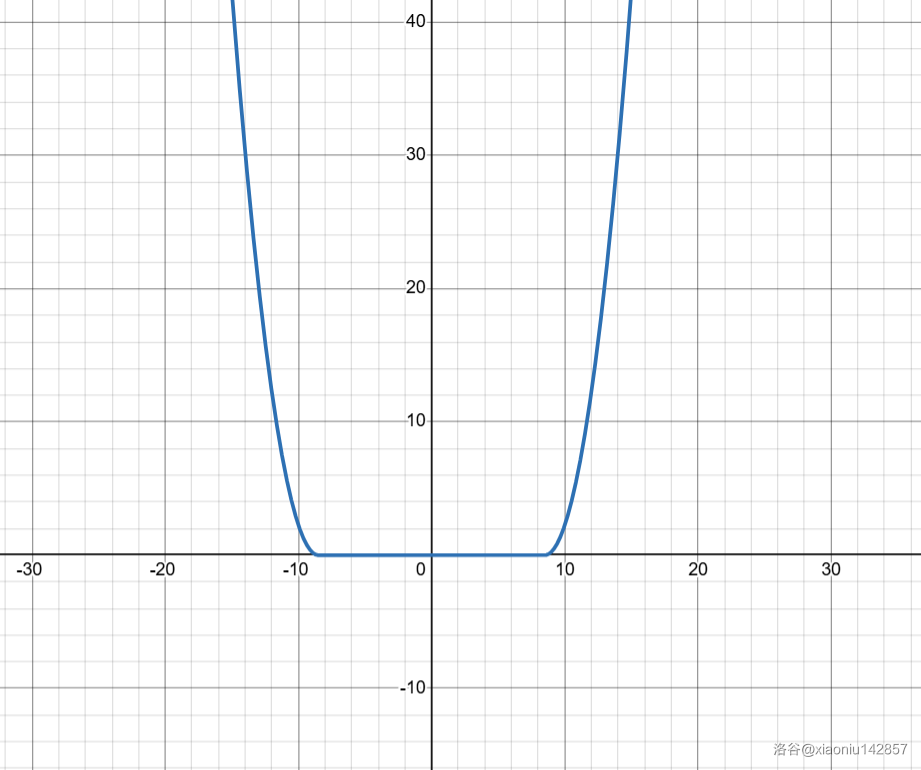
很显然，这是一个单谷函数。

因为单谷函数的和还是单谷函数，所以 \(f(x)\) 也是单谷函数。于是可以直接使用三分法求解最小值。时间复杂度 \(O(n\log n)\)。

Code

#include <iostream>
using namespace std;
const int N=1000;
const int INF=0x3f3f3f3f;
int a[N],n;
int f(int x)
{
    int s=0;
    for(int i=0;i<n;++i)
    {
        if(a[i]<x) s+=(x-a[i])*(x-a[i]);
        else if(a[i]>x+17) s+=(a[i]-x-17)*(a[i]-x-17);
    }
    return s;
}
int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    int l=INF,r=-INF,m1,m2;
    cin>>n;
    for(int i=0;i<n;++i)
    {
        cin>>a[i];
        l=min(l,a[i]);
        r=max(r,a[i]);
    }
    r-=17;
    while(l<r)
    {
        m1=(l+r>>1),m2=m1+1;
        if(f(m1)<f(m2)) r=m2-1;
        else l=m1+1;
    }
    cout<<f(l);
    return 0;
}

Update 2025.2.11：笔误，单峰函数 \(\to\) 单谷函数。
Update 2025.6.15：更换图片，更改图片与文字间距。
Update 2025.6.16：修改部分公式格式。
Update 2025.12.6：微调格式，优化语言表达。