洛谷 P4447 [AHOI2018 初中组] 分组 题解

解题思路

考虑手玩样例找性质。先约定实力值为 \(l\sim r\) 的小组记作 \((l,r)\)。

对于这组样例：

7
1 2 2 3 3 4 5

我们以能力值为横轴画出柱状图。

如果划分成 \((1,5)\) 和 \((2,3)\)，人最少的组有 2 人。

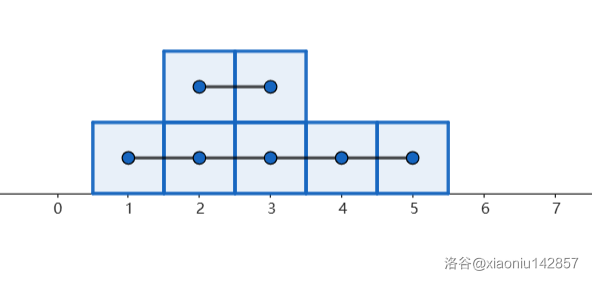
而分成 \((1,3)\) 和 \((2,5)\)，的情况更优。因为这样人最少的组有 3 人。

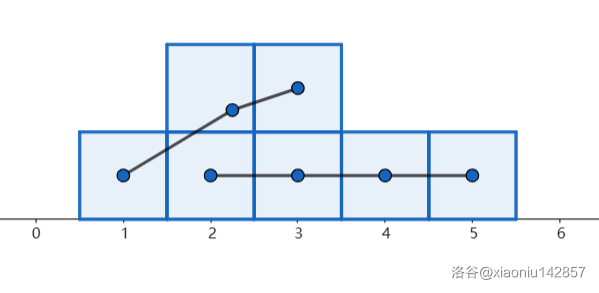
于是我们可以知道，对于任意两组 \((i,j)\) 和 \((k,l)\)，若 \(i\le k\) 且 \(l\le j\)，即 \((i,j)\) 包含 \((k,l)\)，则重组为 \((i,l)\) 和 \((k,j)\) 一定不劣。

因此最优解中的分组两两不包含，\(l\) 更小的组，\(r\) 也一定更小。

考虑用队列维护每组的人数，并依次处理上面柱状图中的每一列。队列中小组的 \(l\) 和 \(r\) 均单调不降。

设当前列高度为 \(h\)，队列长度为 \(len\)，则具体操作如下：

1. 若 \(h\ge len\)，则入队 \(h-len\) 个 \(0\)。
2. 若 \(h<len\)，则弹出 \(len-h\) 个元素并更新答案。

最后队列中的元素整体 \(+1\)，用懒标记 tag 维护即可。

细节：特判高度为 \(0\) 的列，最终必须清空队列并更新答案。

时间复杂度 \(O(n \log n)\)，瓶颈为排序。

Code

#include <bits/stdc++.h>
#define rep(i,a,b) for(int i(a);i<b;++i)
#define rept(i,a,b) for(int i(a);i<=b;++i)
using namespace std;
constexpr int N=1e5+5,INF=2e9;
int a[N],q[N];
int n,ans=INF;
int l,r,tag;
int lst,cur,h;
void calc(){
    // lst：上一列位置
    // cur：当前列位置
    // h：当前列高度
    if(cur-lst>1){  // 中间有高度为0的列
        while(l<r) ans=min(ans,q[l++]+tag);
        rep(i,0,h) q[r++]=-tag;
        ++tag;
        return;
    }
    if(h>=r-l) rep(i,0,h-(r-l)) q[r++]=-tag;
    else rep(i,0,r-l-h) ans=min(ans,q[l++]+tag);
    ++tag;
}
signed main(){
    cin.tie(0)->sync_with_stdio(0);
    cin>>n;
    rept(i,1,n) cin>>a[i];
    sort(a+1,a+n+1);
    cur=a[1],h=1,lst=-INF;
    rept(i,2,n){
        if(a[i]==cur) ++h;
        else{
            calc();
            lst=cur;
            cur=a[i];
            h=1;
        }
    }
    calc();
    while(l<r) ans=min(ans,q[l++]+tag);  // 清空队列，更新答案
    cout<<ans;
    return 0;
}

Update 2025.2.11：修正时间复杂度分析。
Update 2025.6.15：微调图片与文字间距。
Update 2025.6.16：调整公式上下标。
Update 2025.12.6：优化语言表达，修正若干错误，重构代码，感谢 M_Cat 的指正。