网络流量预测入门（一）之RNN 介绍

目录

网络流量预测入门（一）之RNN 介绍

了解RNN之前，神经网络的知识是前提，如果想了解神经网络，可以去参考一下我之前写的博客：数据挖掘入门系列教程（七点五）之神经网络介绍 and 数据挖掘入门系列教程（八）之使用神经网络（基于pybrain）识别数字手写集MNIST

这篇博客介绍RNN的原理，同时推荐大家去看李宏毅老师的课程：ML Lecture 21-1: Recurrent Neural Network (Part I)。基本上看完他的课程，也就没有必要看这篇博客了。

RNN简介

RNN全称Recurrent Neural Network ，中文名为循环神经网络（亦或称递归神经网络）。相信大家在看这篇博客之前都已经简单的了解过RNN。将RNN说的简单一点，就是进行预测（或者回归）的时候，不仅要考虑到当前时刻的输入，还要考虑上一个时刻的输入（甚至有些RNN的变种还会考虑未来的情况）。换句话说，预测的结果不仅与当前状态有关，还与上一个时刻的状态有关。

RNN用于处理时序信息 。而在传统的神经网络中，我们认为输入的 \(x_1,x_2,x_3\)，是相互独立的：比如说在Iris分类中，我们认为鸢尾花的长宽是独立的，之间不存在前后序列逻辑关系。

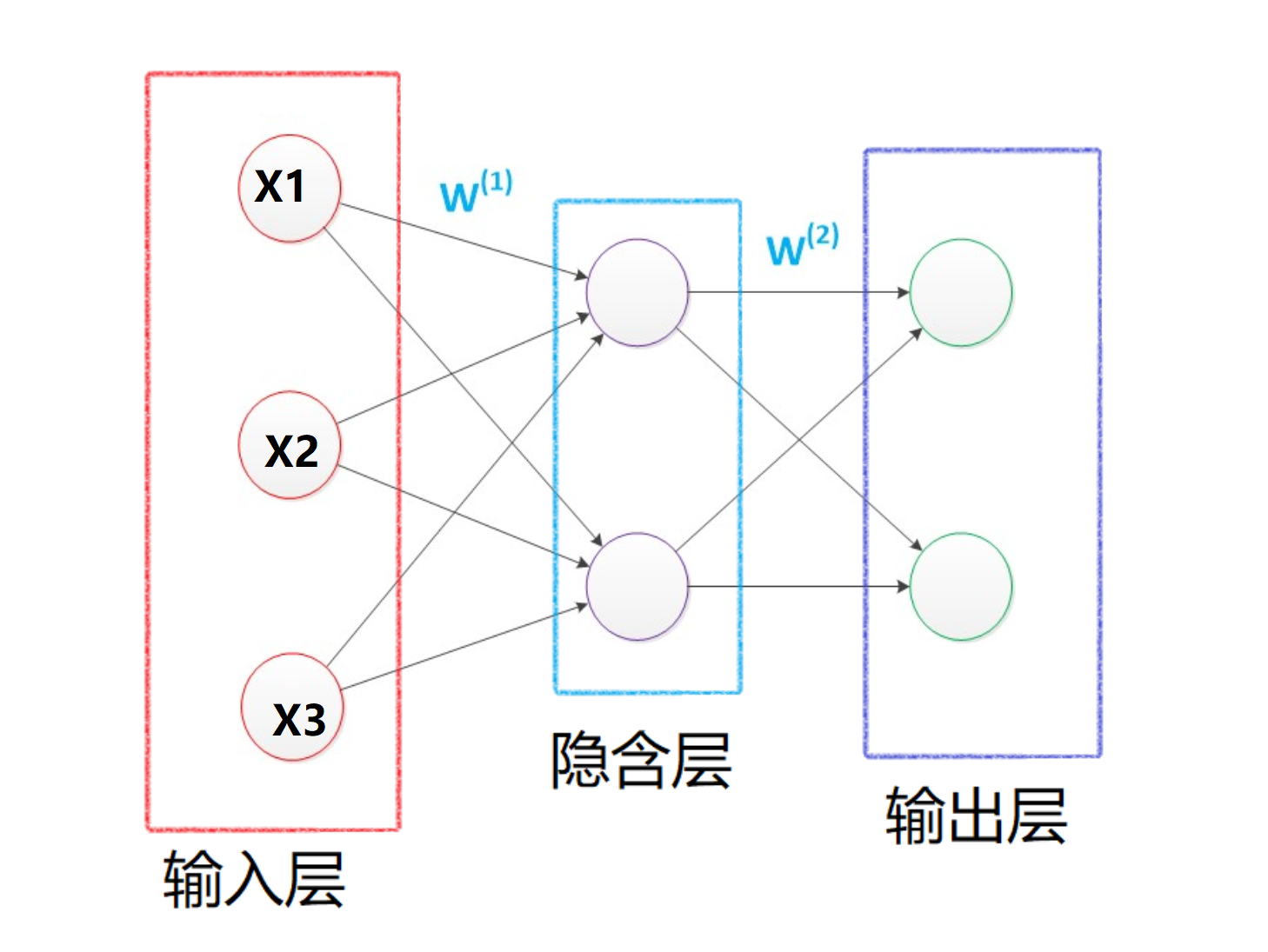
尽管传统的神经网络在预测中能够取得不错的成绩（比如说人脸识别等等），但是对于以下方式情景可能就爱莫能助了。

当我们想要预测一段话“小丑竟是我自____”时，我们必须根据前文的意思来predict。而RNN之所以叫做循环（recurrent），这是因为它的预测会考虑以前的信息。换句话说，也就是RNN具有memory，它“记得”之前计算后的情况。

在知乎全面理解RNN及其不同架构上，说了一个很形象的例子：

以捏陶瓷为例，不同角度相当于不同的时刻：

  • 若用前馈网络：网络训练过程相当于不用转盘，而是徒手将各个角度捏成想要的形状。不仅工作量大，效果也难以保证。
  • 若用递归网络（RNN）：网络训练过程相当于在不断旋转的转盘上，以一种手势捏造所有角度。工作量降低，效果也可保证。

RNN 结构

RNN的原理图，我们最多见的便是如左图所示，但是实际上将它展开，便是如下右图所示。

  1. 在RNN中，我们可以将黄框称之为一个layer，所有的layer的参数在一个batch中是相同的（参数共享），也就是说，上图中的 \(U,W,V\) 等参数在某个batch全部相同。（通过一个batch的训练之后，经过反向传播，参数会发生改变）

  2. Layer的层数根据自己的需要来定，举个例子，比如说我们分析的句子是5个单词构成的句子，那么layer的层数便是5，每一个layer对应一个单词。

  3. 上图既有多个输入\(X_{t-1},X_{t},X_{t+1}\) ， 也可以有多个输出\(O_{t-1},O_{t},O_{t+1}\) , 但是实际上输出可以根据实际的需要而定，既可以为多个输出，也可以只有一个输出，有如下几种：

    Type of RNN Illustration Example
    One-to-one \(T_x=T_y=1\) Traditional neural network
    One-to-many \(T_x=1, T_y>1\) Music generation
    Many-to-one \(T_x>1, T_y=1\) 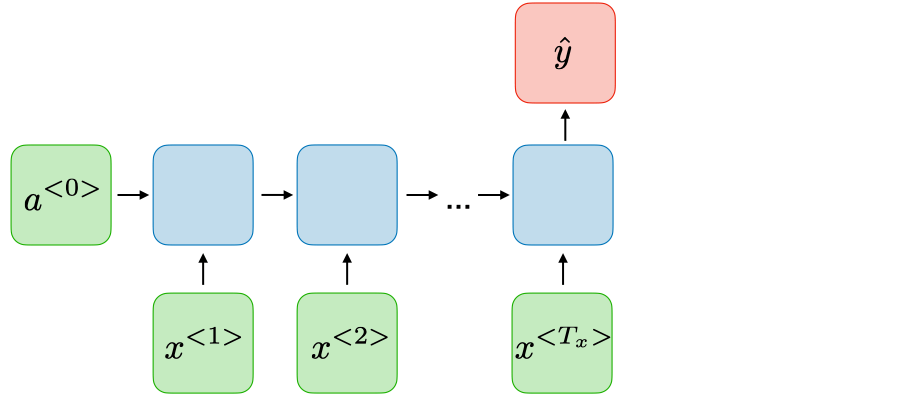Sentiment classification
    Many-to-many \(T_x=T_y\) 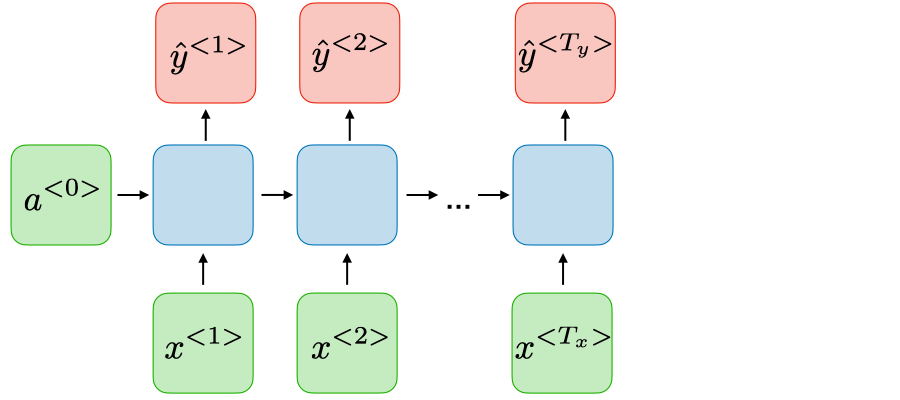Name entity recognition
    Many-to-many \(T_x\neq T_y\) 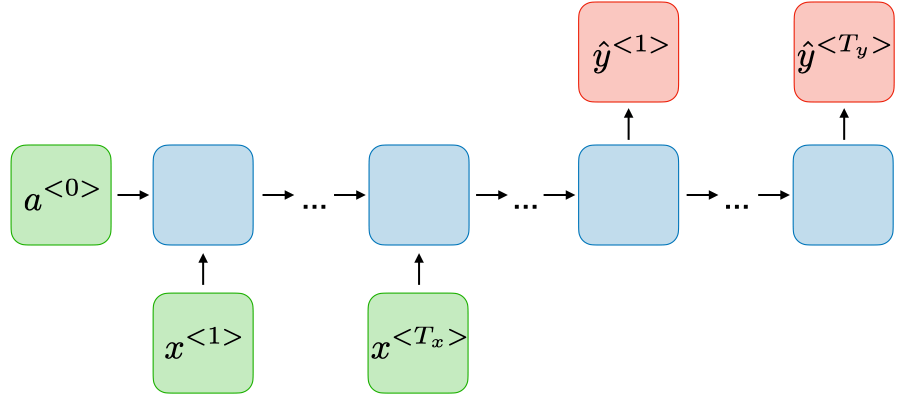Machine translation

Gif图如下所示：

下图是李宏毅老师在课堂上讲的一个例子。

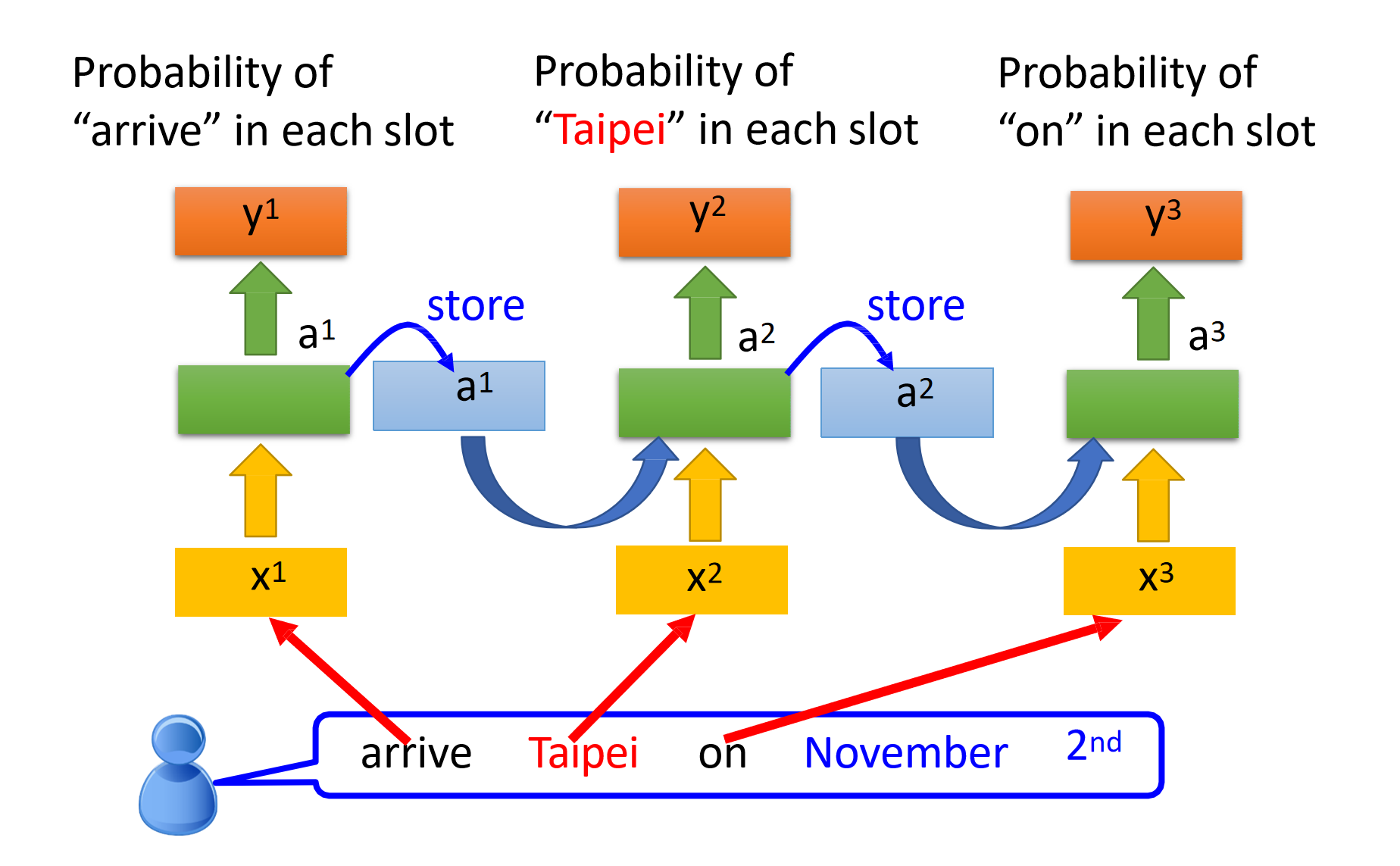
RNN原理

结构原理

下面是来自Recurrent Neural Networks cheatsheet对RNN原理的解释：

\(a^{<t>}\) 和 \(y^{<t>}\) 的表达式如下所示：

\[a^{<t>}=g_{1}\left(W_{a a} a^{<t-1>}+W_{a x} x^{<t>}+b_{a}\right) \quad \text { and } \quad y^{<t>}=g_{2}\left(W_{y a} a^{<t>}+b_{y}\right) \]

  • \(W_{a x}, W_{a a}, W_{y a}, b_{a}, b_{y}\) 在时间上是共享的：也就是说，在一个batch中，无论是哪一个layer，其\(W_{a x}, W_{a a}, W_{y a}, b_{a}, b_{y}\)都是相同的(shared temporally)。当然，经过一个batch的训练之后，其值会因为反向传播而发生改变。

  • \(g_{1}, g_{2}\) 皆为激活函数（比如说tanh，sigmoid）

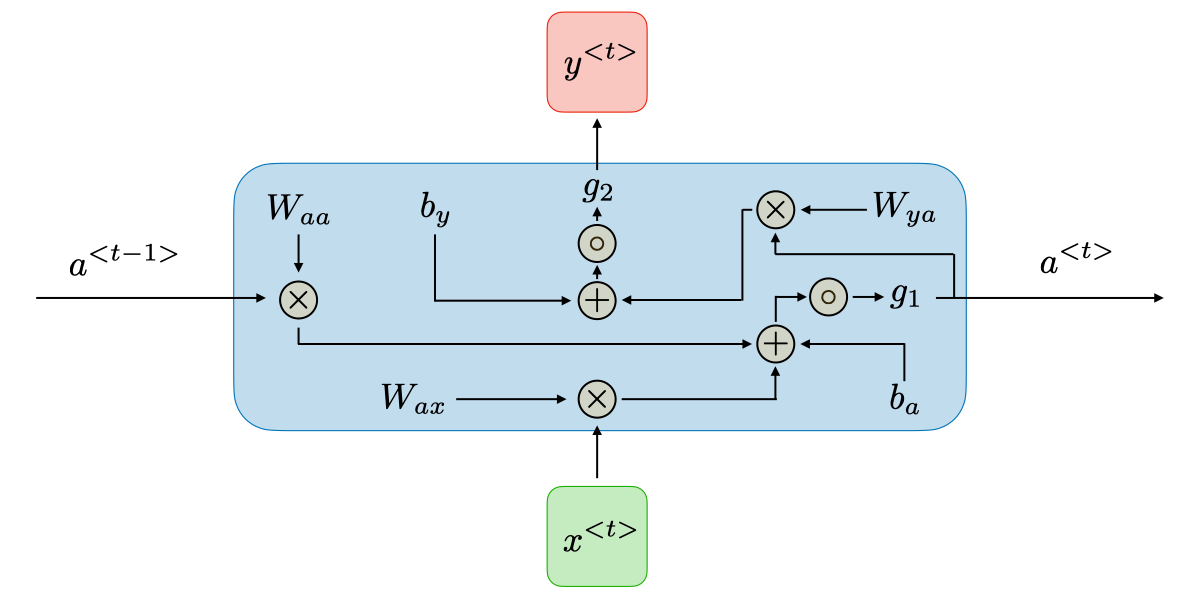
损失函数\(E\)

$ \mathcal{L}$ 为可微分的损失函数，比如交叉熵，其中\(y^{<t>}\)为t时刻正确的词语，\(\hat{y}^{<t>}\)为t时刻预测的词语。

\[\mathcal{L}^{<t>} = \mathcal{L}(\hat{y}^{<t>}, y^{<t>}) \\ {E}(\hat{y}, y)=\sum_{t=1}^{T_{y}} \mathcal{L}^{<t>} \]

反向传播

反向传播目的就是求预测误差 \(E\) 关于所有参数 \((U, V, W)\) 的梯度, 即 \(\frac{\partial E}{\partial U}, \frac{\partial E}{\partial V}\) 和 \(\frac{\partial E}{\partial W}\) 。关于具体的推导可以参考循环神经网络(RNN)模型与前向反向传播算法。

知道梯度后，便可以对参数系数进行迭代更新了。

总结

在上述博客中，简单的对RNN进行了介绍，介绍了RNN作用，以及部分原理。而在下篇博客中，我将介绍如何使用keras构建RNN模型写唐诗。🤭

参考

  1. 什么是 LSTM RNN 循环神经网络 (深度学习)? What is LSTM in RNN (deep learning)?
  2. ML Lecture 21-1: Recurrent Neural Network (Part I)
  3. Recurrent Neural Network (RNN) Tutorial for Beginners
  4. Recurrent Neural Networks cheatsheet
  5. Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs
  6. 全面理解RNN及其不同架构
  7. 神经网络与深度学习(邱锡鹏)
  8. 循环神经网络(RNN)模型与前向反向传播算法
  9. 深度学习框架PyTorch：入门与实践
posted @ 2021-01-25 12:05  渣渣辉啊  阅读(2914)  评论(0)  编辑  收藏  举报