数据挖掘入门系列教程(八)之使用神经网络(基于pybrain)识别数字手写集MNIST
在本章节中,并不会对神经网络进行介绍,因此如果不了解神经网络的话,强烈推荐先去看《西瓜书》,或者看一下我的上一篇博客:数据挖掘入门系列教程(七点五)之神经网络介绍
本来是打算按照《Python数据挖掘入门与实践》里面的步骤使用神经网络来识别验证码,但是呢,验证码要自己生成,然后我又想了一下,不是有大名鼎鼎的MNIST数据集吗,为什么不使用它呢,他不香吗?
MNIST(Mixed National Institute of Standards and Technology database)相信大家基本上都了解过他,大部分的机器学习入门项目就是它。它是一个非常庞大的手写数字数据集(官网)。里面包含了0~9的手写的数字。部分数据如下:

数据集分为两个部分,训练集和测试集。然后在不同的集合中分为两个文件,数据Images文件和Labels文件。在数据集中一个有60,000个训练数据和10,000个测试数据。图片的大小是28*28。

下载数据集
万物始于数据集,尽管官网提供了数据集供我们下载,但是在sklearn中提供了更方便方法让我们下载数据集。代码如下:
import numpy as np
from sklearn.datasets import fetch_openml
# X为image数据,y为标签
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
其中X,y中间既包含了训练集又包含了测试集。也就是说X或者y中有70,000条数据。 那么数据是什么呢?
在X中,每一条数据是一个长为\(28 \times 28=784\)的数组,数组的数据是图片的像素值。每一条y数据就是一个标签,代表这张图片表示哪一个数字(从0到9)。
然后我们将数据进行二值化,像素值大于0的置为1,并将数据保存到文件夹中:
X[X > 0 ] = 1
np.save("./Data/dataset",X)
np.save("./Data/class",y)
然后在Data文件夹中就出现了以下两个文件:

我们取出dataset中间的一条数据,然后转成28*28的格式,如下所示:

数据集既可以使用上面的方法得到,也可以从我的Github上面进行下载(其中dataset数据集因为GitHub文件大小的限制所以进行了压缩,需要解压才能够使用)。
加载数据集
前面的步骤我们下载好了数据集,现在我们就可以来加载数据了。
import numpy as np
X = np.load("./Data/dataset.npy")
y = np.load("./Data/class.npy")
取出X中的一条数据如下所示:

取出y中的一条数据,如下所示:

一切都很完美,但是这里有一个问题,在神经网络中,输出层实际上是这样的:
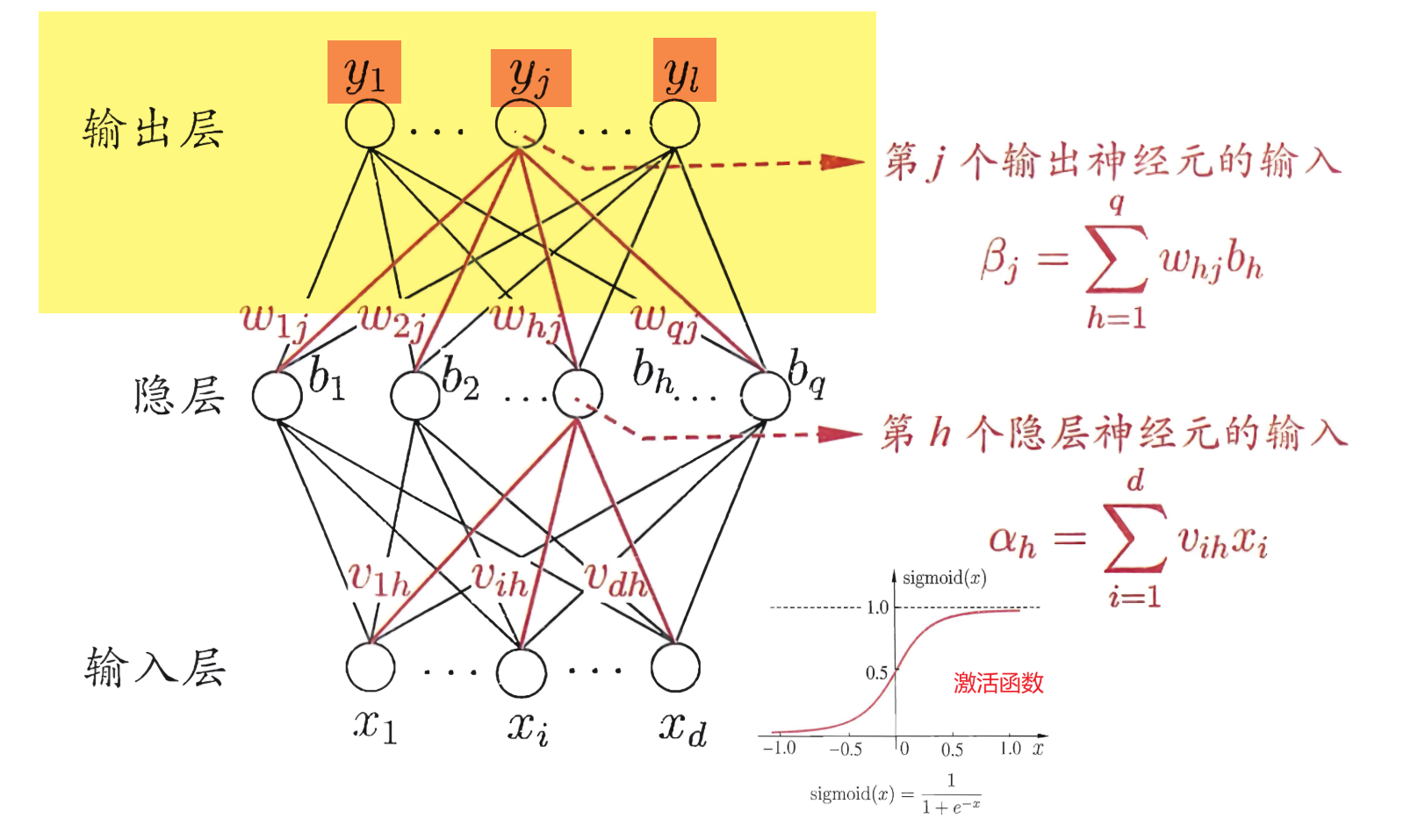
它并不是直接输出某一个结果,而是输出\(y_1,…,y_j,…,y_l\)结果(在MNIST中\(l=10\),因为只有10种数字)。以上面的5为例子,输出层并不是单纯的输出只输出一个数字,而是要输出10个值。那么如何将输出5变成输出10个数字呢?这里我们使用”one hot Encoding“。
One-Hot编码,又称为一位有效编码,主要是采用\(N\)位状态寄存器来对\(N\)个状态进行编码,每个状态都由他独立的寄存器位,并且在任意时候只有一位有效。
以下面的数据为例,每一行代表一条数据,每一列代表一个属性。其中第2个属性只需要3个状态码,因为他只有0,1,2三种属性。这样我们就可以使用100代表0,010代表1,001代表2。
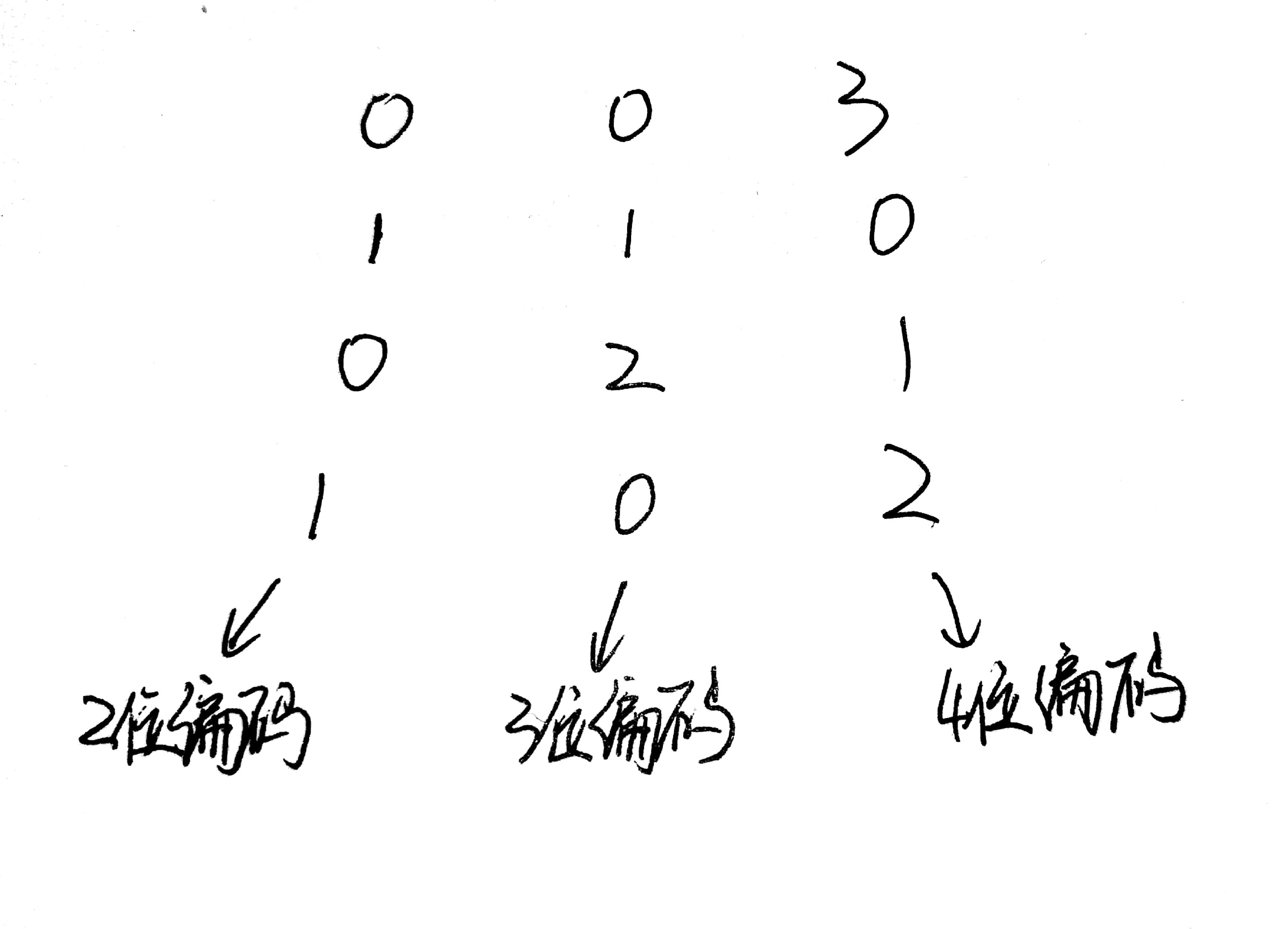
那么这个数据编码后的数据长什么样呢?如下图:

现在我们就可以将前面加载的数据集标签\(y\)进行“one hot Encoding”。
代码如下:
from sklearn.preprocessing import OneHotEncoder
# False代表不生成稀疏矩阵
onehot = OneHotEncoder(sparse = False)
# 首先将y转成行长为7000,列长为1的矩阵,然后再进行转化。
y = onehot.fit_transform(y.reshape(y.shape[0],1))
接着就是切割数据集了。将数据集切割成训练集和测试集。
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(X,y,random_state=14)
在神经网络中,我们使用pybrain框架去构建一个神经网络。但是呢,对于pybrain库,他很与众不同,他要使用自己的数据集格式,因此,我们需要将数据转成它规定的格式。
from pybrain.datasets import SupervisedDataSet
train_data = SupervisedDataSet(x_train.shape[1],y.shape[1])
test_data = SupervisedDataSet(x_test.shape[1],y.shape[1])
for i in range(x_train.shape[0]):
train_data.addSample(x_train[i],y_train[i])
for i in range(x_test.shape[0]):
test_data.addSample(x_test[i],y_test[i])
终于,数据集的加载就到这里结束了。接下来我们就可以开始构建一个神经网络了。
构建神经网络
首先我们来创建一个神经网络,网络中只含有输入层,输出层和一层隐层。
from pybrain.tools.shortcuts import buildNetwork
# X.shape[1]代表属性的个数,100代表隐层中神经元的个数,y.shape[1]代表输出
net = buildNetwork(X.shape[1],100, y.shape[1], bias=True)
这里说有以下“bias”的作用。bias代表的是偏置神经元,bias = True代表偏置神经元激活,也就是在每一层都使用这个这个神经元。偏置神经元如下图,实际上也就是阈值,只不过换一种说法而已。
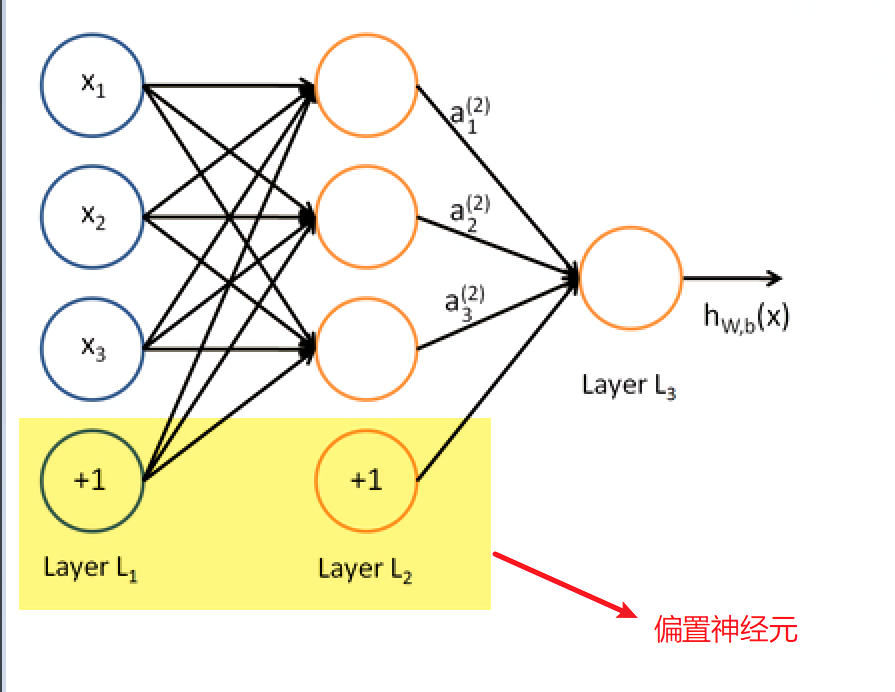
现在我们已经构建好了一个比较简单的神经网络,接下来我们就是使用BP算法去得到合适的权重值了。
反向传播(BP)算法
具体的算法步骤在上一篇博客已经介绍过了,很幸运的是在pybrain中间提供了BP算法的库供我们使用。这里就直接上代码吧。关于BackpropTrainer更加细节的使用可以看官网
from pybrain.supervised.trainers import BackpropTrainer
trainer = BackpropTrainer(net, train_data, learningrate=0.01,weightdecay=0.01)
这里面有几个参数稍微的说明下:
-
net:神经网络
-
train_data:训练的数据集
-
learningrate:学习率,也就是下面的\(\eta\),同样它可以使用lrdecay这个参数去控制衰减率,具体的就去看官网文档吧。
\[\begin{equation}\begin{array}{l} \Delta w_{h j}=\eta g_{j} b_{h} \\ \Delta \theta_{j}=-\eta g_{j} \\ \Delta v_{i h}=\eta e_{h} x_{i} \\ \Delta \gamma_{h}=-\eta e_{h} \\ \end{array}\end{equation} \] -
weightdecay:权重衰减,权重衰减也就是下面的\(\lambda\)
\[\begin{equation} E=\lambda \frac{1}{m} \sum_{k=1}^{m} E_{k}+(1-\lambda) \sum_{i} w_{i}^{2} \\ \lambda \in(0,1) \end{equation} \]
然后我们就可以开始训练了。
trainer.trainEpochs(epochs=100)
epochs也就是训练集被训练遍历的次数。
接下载便是等待的时间了。等待训练集训练成完成。训练的时间跟训练集的大小,隐层神经元的个数,电脑的性能,步数等等有关。
切记切记,这一次的程序就不要在阿里云的学生机上面跑了,还是用自己的机器跑吧。尽管联想小新pro13 i5版本性能还可以,但是还是跑了一个世纪这么久,哎(耽误了我打游戏的时间)。
进行预测
通过前面的步骤以及等待一段时间后,我们就完成了模型的训练。然后我们就可以使用测试集进行预测。
predictions = trainer.testOnClassData(dataset=test_data)
predictions的部分数据,代表着测试集预测的结果:

然后我们就可以开始验证准确度了,这里继续使用F1评估。这个已经在前面介绍过了,就不再介绍了。
F1验证
这里有个地方需要注意,因为之前的y_test数据我们使用one-hot encoding进行了编码,因此我们需要先将one-hot编码转成正常的形式。
# 取每一行最大值的索引。
y_test_arry = y_test.argmax(axis =1)
具体效果如下:

然后使用F1值进行验证。
from sklearn.metrics import f1_score
print("F-score: {0:.2f}".format(f1_score(predictions,y_test_arry,average='micro')))
然后结果如下:

结果只能说还行吧,不是特别的差,但是也不是特别的好。
总结
项目地址:Github。尽管上面的准确度不咋地,只有\(86\%\),但是也还行吧,毕竟也是使用了一层隐层,然后隐层也只有100个神经元。
如果电脑的性能不够的话,可是适当的减少步数和训练集的大小,以及隐层神经元的个数。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号