概述
1.基本概念
- 相机焦距:平行光入射时从透镜中心到光聚焦之焦点的距离,一般使用字母f表示。
- 相机标定就是求解相机的内外参数,畸变参数的过程。
- 内参数:相机内部的几何和光学特性,如焦距,主点位置(图像平面上的点)等
- 外参数:相机坐标系相对于世界坐标系变换过程中的旋转矩阵和平移矩阵,描述了摄像机在三维世界坐标关系,如空间位置和方向。
- 畸变参数:描述图像畸变(如径向畸变,切向畸变)的参数,这些畸变会使得图像中的直线变得弯曲。
- 世界坐标系xyz(world coordinate):由于摄像机与被摄物体可以放置在环境中的任意位置,因此需要在环境中建立一个坐标系,来表示摄像机和被摄物体的位置。这个坐标系称之为世界坐标系
- 相机坐标系xyz(camera coordinate):原点位于镜头光心处,x,y轴分别与像面的两边平行,z轴为镜头光轴,与像平面垂直。
- 图像坐标系xoy:坐标轴的单位一般为毫米。原点为相机光轴与像面的交点,即图像的中心点。x轴与y轴与像面的两边平行。
- 像素坐标系uov: 原点o位于图像的左上角,u,v轴分别与像面的两边平行。像素坐标系中坐标轴的单位是像素(整数值)。像素坐标系和图像坐标系都在成像平面上。
- 齐次坐标(homogeneous coordinate):将n维的向量进行升维用n+1维向量表示,这样可以合并矩阵运算中的乘法和加法,将旋转和平移都统一表示成矩阵乘法的形式,节省计算量。
2.相机标定
- 什么是相机标定:确定光学成像设备(如相机)的输入输出关系
- 相机标定的目的:建立相机成像几何模型并矫正透镜畸变
- 相机标定的方法:比如说张正友标定法
坐标系转换
世界坐标系与相机坐标系的转换
相机坐标系与世界坐标系之间的转换:旋转加上平移
- 旋转:旋转的表示有很多种,比如说旋转矩阵,欧拉角,四元数,轴角,李群与李代数。旋转矩阵用字母R表示。
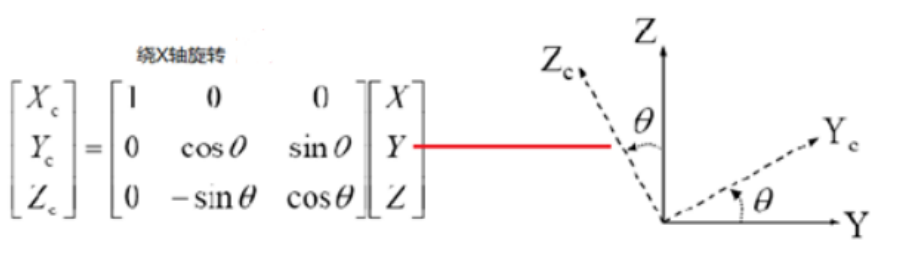
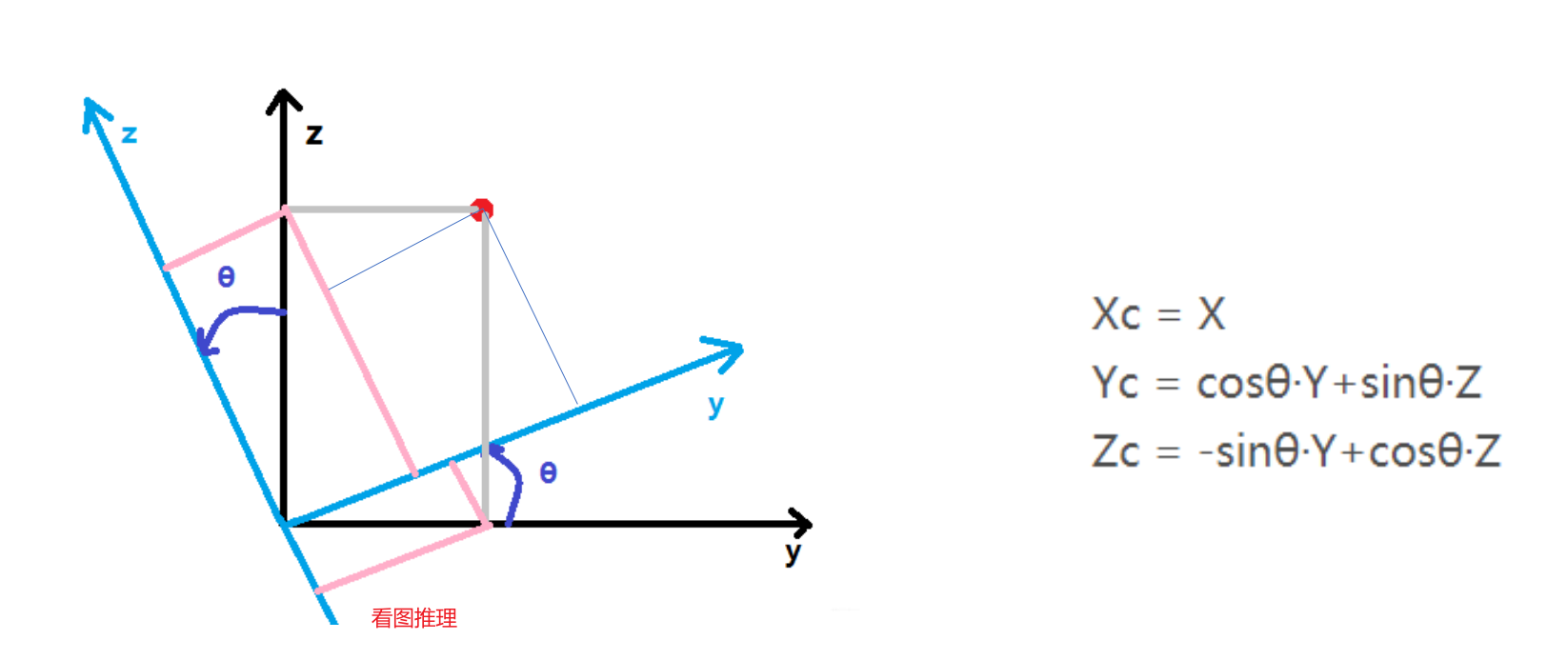
- 绕x轴旋转,矩阵表示如下。绕y,z轴旋转同理。:
![]()
![]()
- 由1推理可得,分别绕x,y,z轴旋转的矩阵如下所示:
![image]()
- 绕x轴旋转,矩阵表示如下。绕y,z轴旋转同理。:
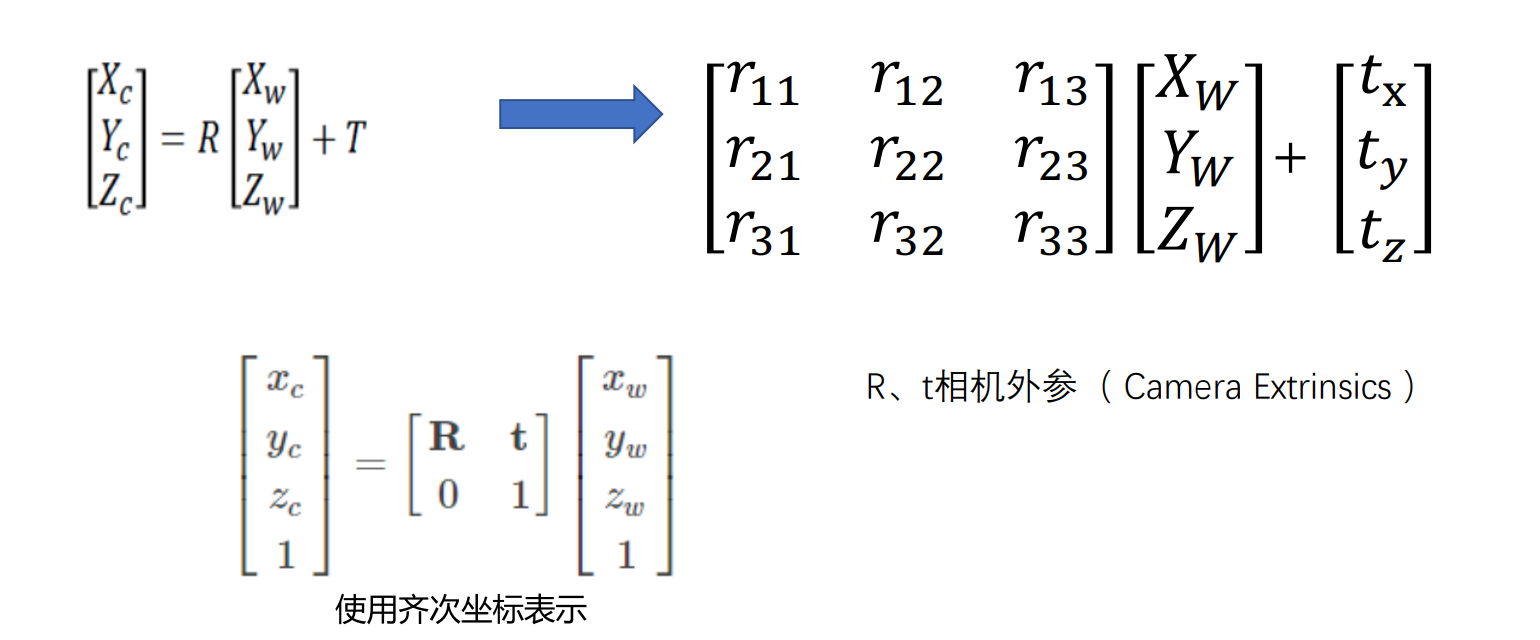
- 平移:旋转之后进行平移,平移向量使用字母T表示。
- 旋转平移以后,就完成了两者坐标系之间的转换。
![]()
图像坐标系与像素坐标系之间的转换
- 转换使用如下运算表示:
![]()
世界坐标系转换为像素坐标系
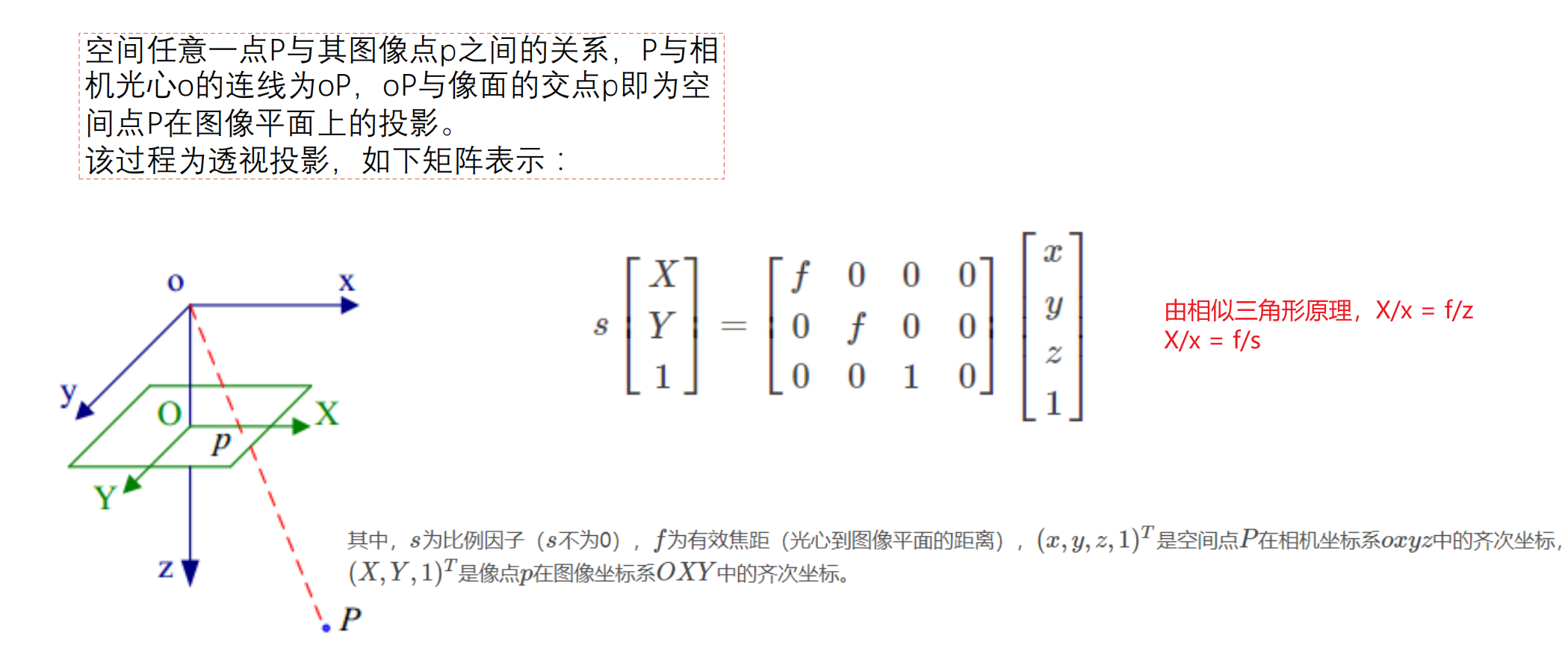
- 相机坐标系转为图像坐标系,使用针孔成像原理:
![]()
- 世界坐标系转为像素坐标系,使用如下运算表示:
![]()
畸变
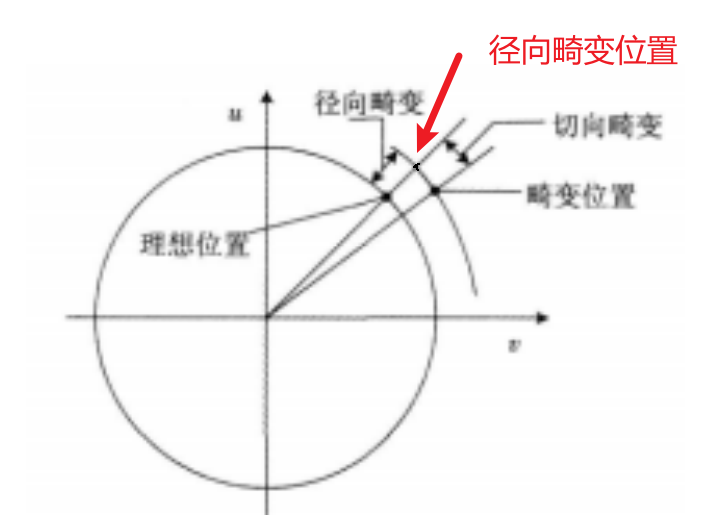
- 畸变:在几何光学中和阴极射线管显示中,畸变是对直线投影的一种偏移。畸变一般分为两类,径向畸变和切向畸变。
- 径向畸变:来自于透镜形状,比如说鱼眼
- 切向畸变:来自于摄像机的组装过程
- 两种畸变公式及示意图如下:
![]()
![]()
相机标定的方法
相机标定法有传统的摄像机标定方法和自标定法
- 传统的摄像机标定方法:在一定的摄像机模型下,基于特定的实验条件如形状和尺寸已知的参照物,进行图像处理,数学变换等技术求取相机内外参数。传统的摄像机标定方法有:
- 利用最优化算法的标定方法
- 利用摄像机变换矩阵的标定方法
- 考虑畸变补偿的两步法
- 张正友标定法
- 自标定法:这种方法不依赖参照物,利用摄像机本身参数之间的约束关系或者周围图像与图像之间的对应关系来标定。通常有:
- 基于Krupa方程
- 分层逐步标定法
- 基于二次曲面自标定
张正友标定法
- 一种利用平面棋盘格(平面棋盘是一块由黑白方块间隔组成的标定板)进行相机标定的实用方法。该方法介于摄影标定法和自标定法之间,既克服了摄影标定法需要的高精度三维标定物的缺点,又解决了自标定法鲁棒性差的难题。标定过程仅需使用一个打印出来的棋盘格,并从不同方向拍摄几组图片即可,任何人都可以自己制作标定图案,不仅实用灵活方便,而且精度很高,鲁棒性好。
- 单应性变换:描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵。在将世界坐标系转化为像素坐标系中,单应性矩阵如下H所示,M为内部参数,s为伸缩系数,(r1,r2,t)为外部参数。
![]()
- 在opencv中存在相应的接口计算单应矩阵


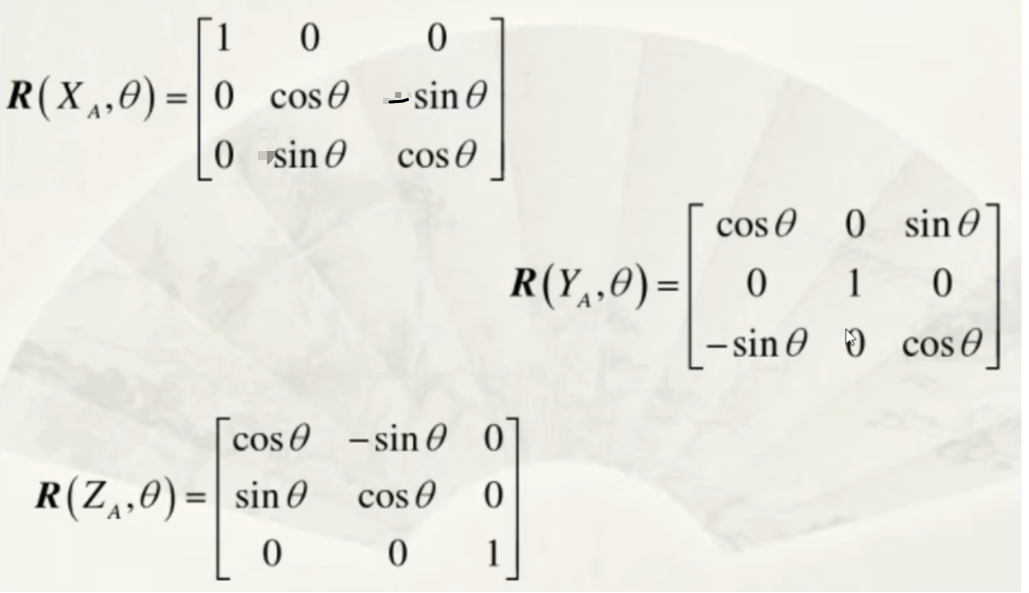



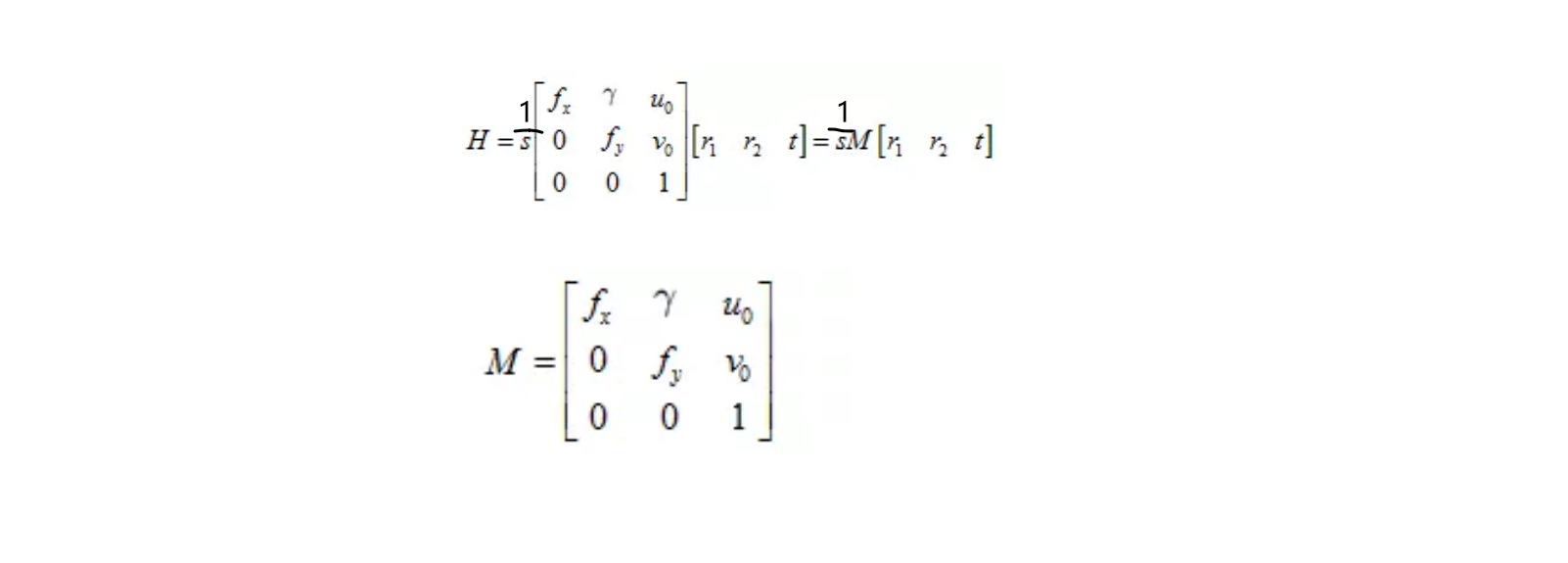

 浙公网安备 33010602011771号
浙公网安备 33010602011771号